Ship's Trajectory Planning for Collision Avoidance at Sea Based on Ant Colony Optimisation

Abstract

Swarm Intelligence (SI) constitutes a rapidly growing area of research. At the same time trajectory planning in a dynamic environment still constitutes a very challenging research problem. This paper presents a new approach to path planning in dynamic environments based on Ant Colony Optimisation (ACO). Assumptions, a concise description of the method developed and results of real navigational situations (case studies with comments) are included. The developed solution can be applied in decision support systems on board a ship or in an intelligent Obstacle Detection and Avoidance system, which constitutes a component of Unmanned Surface Vehicle (USV) Navigation, Guidance and Control systems.

1. INTRODUCTION

The problem of collision avoidance in dynamic environments occurs, for example, in robotics, military, aerospace and maritime industries. Example applications that need to deal with the path-planning problem in a dynamic environment include decision support systems, unmanned vehicles, mobile robots and manipulators.

Planning of the object motion is a growing area of research. Many different approaches to solving the path planning problem have been developed so far. These methods can be divided into two categories: path planning in static environments and in dynamic environments. Static environments contain only stationary obstacles, while in dynamic environments there are also moving obstacles.

The scope of this research covers Swarm Intelligence (SI), specifically Ant Colony Optimisation (ACO), which is classified within this group of methods. Approaches to solving path-planning problems based on ACO are found in the literature. However, most of the solutions deal with determining the object transition path in a static environment. Brand et al. (2010) have presented the application of ACO to robot path planning. In this approach the optimal path is first searched for between the initial and final position in the obstacle-free environment. After that, static obstacles are added and the optimal path is recomputed. The objective function associated with each solution is defined as the total path length. The environment is discretized into a grid of cells. The ant occupying a current cell can choose an adjacent cell by moving in four directions: up, down, left and right. The total path length is defined as a number of cells used by an ant to reach the final position. The maximum number of iterations constitutes a termination condition. Simulation tests have been performed for a grid size of 20×20, 30×30 and 40×40 cells. The results presented have confirmed that the algorithm is capable of determining a safe path in an environment with static obstacles.

A similar approach for solving a mobile robot path-planning problem has been reported by Lee and Lee (2010). In this study a modified version of the ACO algorithm was introduced, called Heterogeneous ACO (HACO). A series of modifications have been developed in this solution with respect to the basic ACO approach. These improvements include a different function defining the manner in which artificial ants choose their next move. The formula, called the pheromone trail update rule, which is used for computing a value deposited by the ants on their paths during problem solving, has been also modified. Another significant difference between ACO and HACO is the use of different species of artificial ants. Heterogeneous ants differ in sight and speed. The results of a comparative analysis between ACO and HACO have confirmed that better solutions are obtained with the use of the second approach, which means smooth and straight-line paths even for more complex environments in a shorter computation time.

Mingxin et al. (2010) have reported a hybrid method applied to mobile robot path planning in a static environment, combining ACO and the Immune Network Algorithm (INA). In this approach an immune network is first constructed, where stimulation and suppression between an antigen and an antibody occurs. An antigen represents an environment surrounding a robot, while an antibody expresses a robot action. In the second step of the algorithm artificial ants are put on the network to search for an optimal path.

Escario et al. (2012) have introduced an approach based on ACO to optimise manoeuvres of an Unmanned Surface Vessel (USV) and called their solution Ant Colony Extended due to a number of modifications applied to the original version of ACO. One of these modifications is similar to that proposed by Lee and Lee (2010) and uses a heterogeneous population of ants called patrollers and foragers. Patrollers are responsible for exploration; their task is to find new solutions. The foragers' task is exploitation, which is searching for solutions similar to those already found. The method uses a dynamical model of a vessel in three degrees of freedom, which includes surge, sway and yaw motions. The state variables include the ship's position coordinates (x and y), the ship's heading, the ship's linear velocities in surge and sway directions and the ship's angular velocity. The action variables are represented by the force exerted by a waterjet and a waterjet orientation. The results presented include the USV's trajectories in the open sea and in situations with the presence of static obstacles, such as port manoeuvres, navigation through narrow channels or shallow waters.

In Tsou and Hsueh (2010) ACO has been applied to ship collision avoidance route planning. Results concerning an encounter situation with one moving obstacle and with four moving obstacles have been presented. Multi-ship encounter situations are decomposed into single encounter situations with one target ship. The collision avoidance route is calculated for the encounter situation with the target ship with the highest collision risk. If the determined path imposes a risk of collision on other target ships, it has to be corrected. In this approach a comparison of the ACO and genetic algorithms has been presented and it has been stated that the ACO algorithm has better performance with respect to execution efficiency and execution results.

Based on the current state of the art analysis concerning the problem of determining the object transition path, summarised in Table 1, it is apparent that the algorithms developed so far do not exhaust the possibilities of research in this field. Solutions developed so far in a large part cover the problem considered in a static environment. The determination of an optimal transition path of an object in an environment in which moving obstacles occur, even though some methods can be found in the current literature, still constitutes a very challenging research task. Methods presented in the literature have some limitations, for example there is no information about the reproducibility of results. The results presented of simulation tests cover simple situations with few dynamic obstacles and some results include only one example solution.

Table 1. Summary of the most interesting ACO-based path planning algorithms found in recent literature.

This paper presents a new ACO-based solution of a ship's trajectory planning problem in a collision situation at sea. The paper is organised as follows: Section 2 describes the safe ship control process in a collision situation at sea with all of the adopted assumptions and presents the developed ACO algorithm. Section 3 includes results of simulation tests performed with input data of real navigational situations with the evaluation of the method efficiency. The last section summarises the reported approach and describes achievements and limitations of the solution.

2. METHOD

2.1. Environment representation

The navigational environment (E) has boundaries defined by Equation (1) and consists of free space (Efree) and obstacles space (Eobs), which includes static and dynamic obstacles. The environment is presented in Figure 1 and is defined by Equation (2). The obstacles space consists of a set of static restrictions (Estat) and dynamic restrictions (Edyn(t)), evolving in time, as defined by Equation (3).

(1)$${\rm E} = \{ ({\rm x},{\rm y}) \in {\rm R}^2 :{\rm k} \le {\rm x} \le {\rm l},\; {\rm m} \le {\rm y} \le {\rm n}\} $$

(2)$${\rm E} = {\rm Efree}\, \cup \,{\rm Eobs}{\kern 1pt} $$

(3)$${\rm Eobs} = {\rm Estat}\, \cup \,{\rm Edyn}({\rm t})$$

Figure 1. Navigational environment representation.

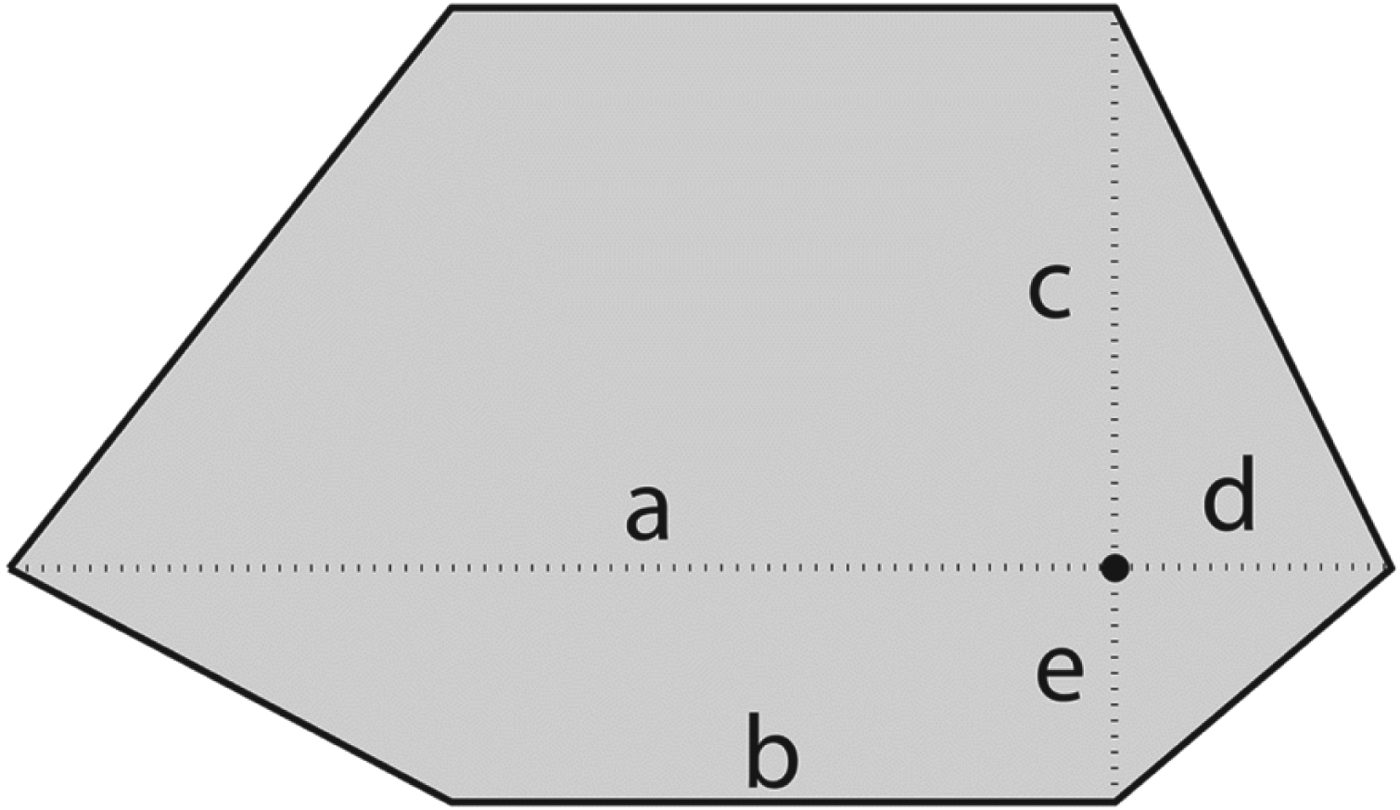
Static obstacles such as land, shallow waters, canals and fairways are represented by concave and convex polygons. Dynamic obstacles are represented by the target ship domain in the form of a hexagon, as presented in Figure 2, inspired by Smierzchalski and Michalewicz (2000). However, it is also possible to apply in the algorithm other shapes of the target ship domain, for example in the form of a circle, an ellipse or a parabola. The target ship domain dimensions enforce the International Regulations for Preventing Collisions at Sea (COLREGs) compliance of the determined own ship trajectory (Cockcroft and Lameijer, 2012). Extension of the target ship domain in the bow direction in a crossing situation (rule 15 of COLREGs) requires own ship to pass astern of the target vessel. Enlargement of the target ship domain starboard side in a head-on situation (rule 14 of COLREGs) induces a course alteration of own ship to starboard.

Figure 2. Target ship hexagon domain.

2.2. Problem definition

The ship's trajectory is determined as a set of waypoints as shown in Figure 1. Each waypoint is defined by the geographical coordinates (latitude – x and longitude – y). The solution of the ship's collision avoidance problem is the trajectory from the current ship's position to the next waypoint, which enables the own ship to avoid collision with other ships and static obstacles with the smallest possible deviation from the given path.

It is assumed that the target ships do not change their courses and speeds. The process of collision avoidance at sea is described with the use of the kinematic model of ship motion. The state equations of the control process are defined by Equations (4), where the state variables are: x₁=x, x₂=y, x_2·j+1=x_j, x_2·j+2=y_j, for (j=1, … , m) and m is the number of target ships identified in the environment. The decision variable u is represented by the own ship course Ψ. An example collision situation defined by Equations (4) is shown in Figure 3.

Figure 3. An example collision situation at sea defined by Equations (4).

Two types of the safe ship control process are distinguished, for which the aim is to:

• • avoid a collision and return to the given final course, for the situation in the open sea

• • avoid a collision and return to the given final point of the trajectory, for the situation in restricted waters.

The developed algorithm solves the ship's collision avoidance task, for which the final condition is the return to the given waypoint of the trajectory.

(4)$$\eqalign{& {\rm \dot x}_{\rm 1} = {\rm V} \cdot \sin {\rm u}({\rm t}) = \; {\rm V} \cdot \sin {\rm \psi} ({\rm t}) \cr & {\rm \dot x}_{\rm 2} = {\rm V} \cdot \cos {\rm u}({\rm t}) = \; {\rm V} \cdot \cos {\rm \psi} ({\rm t}) \cr & {\rm \dot x}_{{\rm 2} \cdot {\rm j} + 1} = {\rm V}_{\rm j} \cdot \sin {\rm \psi} _{\rm j} ({\rm t})} $$

The dynamic properties of the own ship during a course alteration manoeuvre are taken into account by the use of the manoeuvre time. The manoeuvre time t_m, as expressed by Equation (5), is a complex function of the rudder angle δ, the speed of the own ship V and the loading condition L. The manoeuvre time is defined as the time of the own ship movement from the beginning of the manoeuvre to the moment when the value of the new course has been reached. As is shown in Figure 4, it is the time of passage of the line segment A₀A₁ and the time of passage of the curve A₁A₂ with the angular speed ω.

(5)$${\rm t}_{\rm m} = {\rm f}(\rm \delta, {\rm V},{\rm L})$$

Figure 4. Diagram of the own ship motion during the course alteration manoeuvre.

The angular speed of the own ship ω is determined experimentally during the turning manoeuvre trials. The manoeuvre time is approximated, based upon the work by Lisowski (2010), by Equation (6), where t₀₁ is the time of passage of the line segment A₀A₁ and ΔΨ is the course alteration value.

(6)$${\rm t}_{\rm m} = {\rm t}_{01} + \displaystyle{{{\rm \Delta \Psi}} \over {\rm \omega}} - \displaystyle{1 \over {\rm \omega}} {\rm tg}\displaystyle{{{\rm \Delta \Psi}} \over 2}$$

In the algorithm, the trajectory of the own ship during a course alteration manoeuvre is approximated by the line segments instead of a curve. Determination of the course alteration manoeuvre is performed by the calculation of a kinematic manoeuvre at the moment t₁=t₀+t_m, where t₀ is the moment of the beginning of the manoeuvre – the ship is at point A₀, t_m is the time of passage of line segment A₀B and t₁ is the time, when the own ship is at point B.

2.3. ACO-based algorithm for calculations of ship's safe trajectory

ACO, as defined by Bonabeau et al. (1999), is an attempt to build an algorithm inspired by the collective behaviour of a colony of insects or other animal communities. An ant colony constitutes a decentralised system characterised by self-organisation, flexibility and robustness. It is composed of a number of relatively simple interacting individuals and has a high capability of solving many problems such as foraging or building and expanding a nest. These problems are very similar to problems occurring in engineering and computer science. The knowledge gained during observations of the behaviour of ant colonies led to the development of ACO. This approach was been introduced by Bonabeau et al. (1999) and has been applied to a combinatorial optimisation problem of finding the shortest route between a number of cities, called the Traveling Salesman Problem (TSP). ACO has been inspired by the discovery of the mechanism of indirect communication observed in ant colonies. While moving between a food source and a nest ants deposit some chemical substance on the ground, called the pheromone trail. Other ants follow the path, where the pheromone trail concentration is greater. This phenomenon, where the behaviour of individuals affects the environment, which in turn affects the behaviour of other individuals, is called stigmergy. Ants utilise this mechanism to find the shortest path between a food source and their nest. In ACO a group of agents, called artificial ants, realise this trail-laying and trail-following behaviour by depositing a virtual pheromone trail. This action strengthens parts of good solutions, which enables the algorithm to find better solutions in subsequent iterations.

The description of the ACO algorithm for collision avoidance at sea is presented below and compared with the most relevant method developed recently by Tsou and Hsueh (2010). A summary of the algorithm comparison is shown in Table 2. The ACO algorithm for collision avoidance at sea is composed of the following steps, as presented at the flowchart in Figure 5:

1. (1) The collection of the following integrated input data from ARPA and AIS:

   • • the course and the speed of the own ship

   • • the course and the speed of the j-th target ship

   • • the bearing of the j-th target ship

   • • the distance of the j-th target ship from the own ship

   • • the data related to static navigational obstacles (shoals, shorelines, buoys).

   ARPA (Automatic Radar Plotting Aid) is a system that calculates motion and approach parameters of objects tracked with the use of a marine radar. AIS (Automatic Identification System) also constitutes a system used on ships for identifying and locating other vessels in the vicinity of an own ship. In the AIS system data is transmitted with the use of the VHF transmitter built into the AIS transponder. In the approach reported by Tsou and Hsueh (2010) static obstacles are not taken into account and a circle domain is used around the own ship instead of a hexagon domain around the target ship.

2. (2) The calculation of the relative course, speed and bearing of the target ships with respect to the own ship.

3. (3) Checking for every target ship if it is a dangerous object – whether it intersects its course with the course of the own ship.

4. (4) Building a construction graph, as shown in Figure 6. The graph vertices reflect the possible own ship positions, taking into account all static and dynamic constraints.

   In the solution presented by Tsou and Hsueh (2010) a construction graph includes vector format data instead of grid format data representing the own ship waypoints.

   The following four parameters are used in their method instead of the longitude and latitude of possible waypoints:

   • • the required time to the turning point

   • • the required collision avoidance angle for passing the target ship at the safe distance

   • • the time between the turning to collision avoidance and the turning to navigational restore

   • • the limited angle upon turning of navigational restore.

5. (5) The ACO calculations procedure, which is composed of the following steps:

   • • the data initialisation

   • • the solution construction

   • • the pheromone trail update.

6. (6) The graphical presentation of the solution.

Figure 5. Flowchart of the ACO-based algorithm for collision avoidance at sea.

Figure 6. Explanatory diagram of a construction graph used in the ACO algorithm for ship collision avoidance.

Table 2. The comparison of ACO-based methods for the collision avoidance at sea.

2.3.1. Data initialisation

In this procedure the following parameters of the ACO algorithm are initialised:

• • the pheromone trail amount for all vertices (τ₀)

• • the α and β coefficients used in the formula calculating ant's next move probability

• • the pheromone evaporation rate (ρ)

• • the number of ants

• • the maximum number of ant's steps

• • the number of iterations.

2.3.2. Solution construction

Every ant starts to build its path from the starting vertex of the graph (wp₀(x₀, y₀)), which constitutes the current position of the own ship. An ant constructs its path until it reaches the ending vertex of the graph (wp_e(x_e, y_e)) – the defined final point of the trajectory or the maximum number of steps. At each stage the ant chooses the next own ship position (the vertex on the graph) on the basis of the action choice rule. The choice of the next vertex depends on the value of the pheromone trail (τ_wpj(t)) on the neighbouring vertex and the heuristic information called visibility (η_wpij). The heuristic information is the inverse of the distance between the current vertex (i) and the neighbouring vertex (j). The probabilistic choice of the next vertex works similarly to the roulette wheel selection procedure used in the evolutionary algorithms.

This process is composed of the following stages:

• • summing the probability of the selection of individual vertices

• • the random selection of q number in the range [0,1]

• • the passage of the neighbouring vertices until the sum of selection probabilities for previously visited vertices is greater than the number (q); reaching this condition means the choice of that vertex.

(7)$${\rm P}_{{\rm wp}_{{\rm ij}}} ^{{\rm ant}} ({\rm t}) = \displaystyle{{\lsqb {{\rm \tau} _{{\rm wp}_{\rm j}} ({\rm t})} \rsqb^{\rm \alpha} \cdot \lsqb {{\rm \eta} _{{\rm wp}_{{\rm ij}}}} \rsqb^{\rm \beta}} \over {\mathop \sum \nolimits_{{\rm l} \in {\rm wp}_{\rm i}^{{\rm ant}}} \lsqb {{\rm \tau} _{{\rm wp}_{\rm l}} ({\rm t})} \rsqb^{\rm \alpha} \cdot \lsqb {{\rm \eta} _{{\rm wp}_{{\rm il}}}} \rsqb^{\rm \beta}}} $$

In Equation (7), based on Dorigo and Stutzle (2004), for calculating the probability of choosing the next vertex, there are two factors. If the (α) coefficient equals zero the most likely choice is the closest vertex, whereas if the (β) coefficient is equal to zero only the pheromone trail is taken into account, which results in rather unsatisfactory solutions. The feasible neighbourhood of an ant when being at vertex (i) is expressed by (wp_i^ant). The explanatory diagram of Equation (7) is shown in Figure 7.

Figure 7. Explanatory diagram of the equation for calculating ant's next move probability.

2.3.3. Pheromone trail update

When all of the ants in the iteration of the algorithm have finished their paths, the pheromone trail amount is updated according to Equation (8), which consists of two stages:

• • the pheromone evaporation

• • the pheromone deposit

(8)$${\rm \tau} _{{\rm wp}_{\rm j}} ({\rm t} + 1) = ({\rm 1} - {\rm \rho} ) \cdot {\rm \tau} _{{\rm wp}_{\rm j}} (\rm t) + \mathop \sum \limits_{{\rm ant} = 1}^{\rm m} \Delta {\rm \tau} _{{\rm wp}_{\rm j}} ^{{\rm ant}} (\rm t)$$

At the first stage the pheromone evaporation is performed, which means reducing the pheromone trail for all vertices of a constant value. Evaporation of the pheromone trail is the mechanism to “forget” the ants' bad decisions.

Then, the pheromone deposit is carried out, which means adding a certain value to all vertices belonging to the paths constructed by ants in the iteration.

Through this mechanism, the vertices that constitute parts of the shortest paths receive more pheromone trail and the likelihood of their selection by the ants in subsequent iterations increases. Before the start of the next iteration, the best solution found so far is saved.

2.3.4. The objective function

The algorithm determines only feasible solutions. The termination condition is defined as the maximum number of iterations or the maximum computational time. The optimality criterion is expressed as the shortest path determined by ants. The objective function is defined by Equation (9), similarly to the Tsou and Hsueh (2010) approach, as the length of the determined trajectory. The aim of the safe ship trajectory optimisation process is the minimisation of the objective function.

(9)$${\rm I} = \mathop \sum \limits_{{\rm i} = 1}^{{\rm N} - 1} \sqrt {(\rm x_{{\rm i} + 1} - \rm x_{\rm i} )^2 + (y_{{\rm i} + 1} - y_{\rm i} )^2} \to \min $$

3. RESULTS

The developed algorithm has been implemented in the MATLAB programming language, mainly due to the integrated graph-plotting and dynamic simulation features, which allow an easy graphical presentation of the results. The algorithms have been examined with the use of several dozen test cases. The input data of the examined navigational scenarios constitute information describing real navigational situations registered with the use of the Marine Traffic service available at http://www.marinetraffic.com/. Two example situations have been chosen to prove the problem solving capability of the developed algorithm and the efficiency of the received solutions. The calculations have been conducted with the use of a PC with an Intel Core i5 M430 2·27 GHz processor, 2GB RAM, 32-bit Windows 7 Professional.

The following values of parameters used in the ACO calculations have been used in the presented simulation tests: τ₀=1, ρ=0·1, α=1, β=1, number of iterations=20 and number of ants=10. The following dimensions of the hexagon domain have been used for the simulation tests: a – distance towards bow=1 nm, b – distance of amidships=0·6 nm, c – distance towards starboard=0·6 nm, d – distance towards stern=0·25 nm, e –distance towards port side=0·25 nm.

3.1. Scenario 1

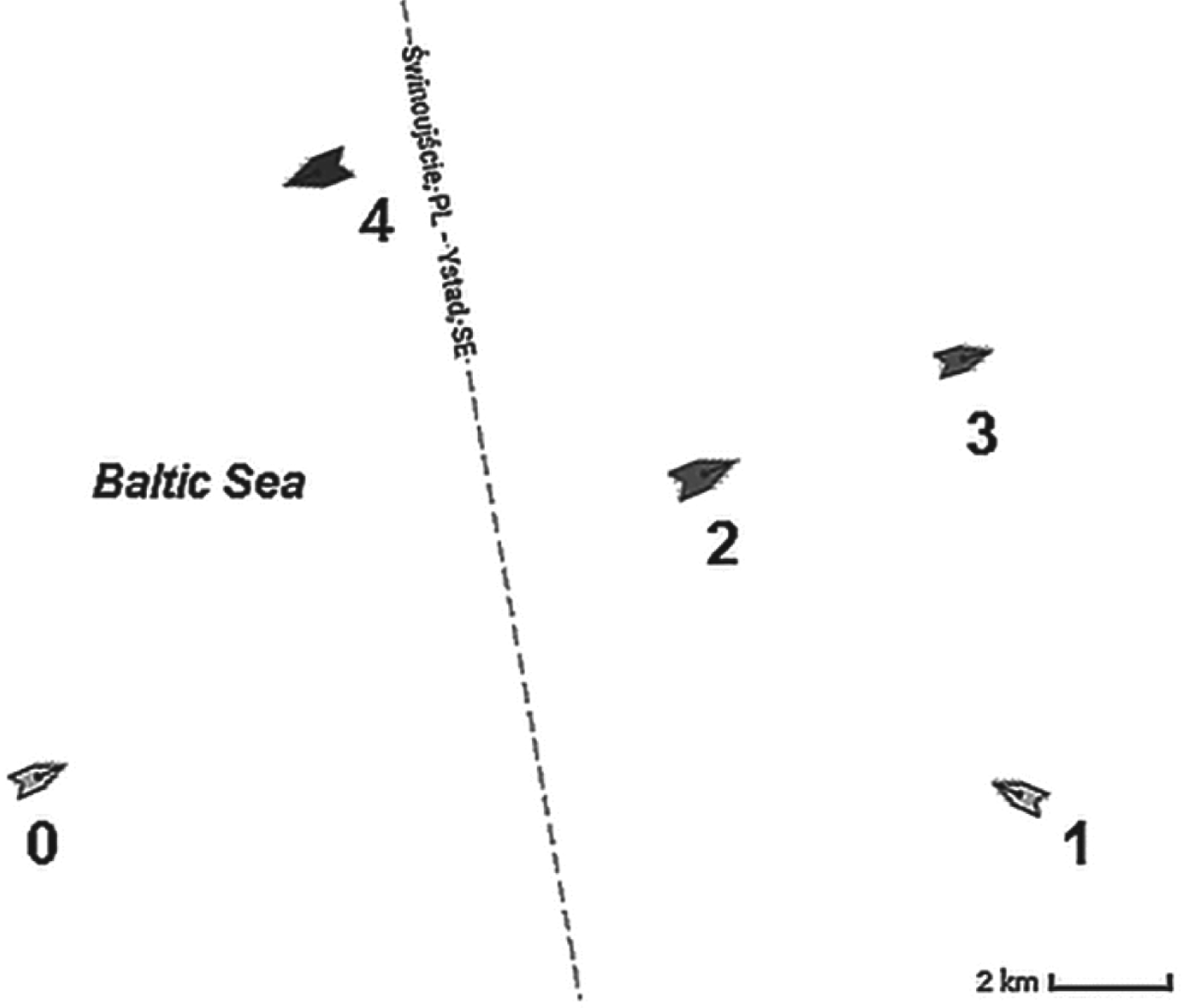
The first example scenario presents an encounter of the own ship (marked with the number zero) with four target ships marked with the numbers from one to four. The situation was registered in the Baltic Sea. Figure 8 shows this navigational situation registered by the Marine Traffic service. The situation is presented in the north up orientation, which means that the graph vertical axis represents the direction of true north. The data input to the algorithm are shown in Table 3. The first column includes the numbers indicating the ships as marked in Figure 8. The second column contains the courses of the own ship and the target ships in degrees, while in the third column the own ship and target ships speeds in knots are listed. The fourth column includes the bearings of the target ships' relative to true north in degrees, what means that the direction toward the geographic north pole is used as a reference point, as presented in Figure 3. The last column contains the ranges of the target ships with respect to the own ship in nautical miles.

Figure 8. Navigational Scenario 1 (source: http://www.marinetraffic.com/).

Table 3. Navigational data of Scenario 1.

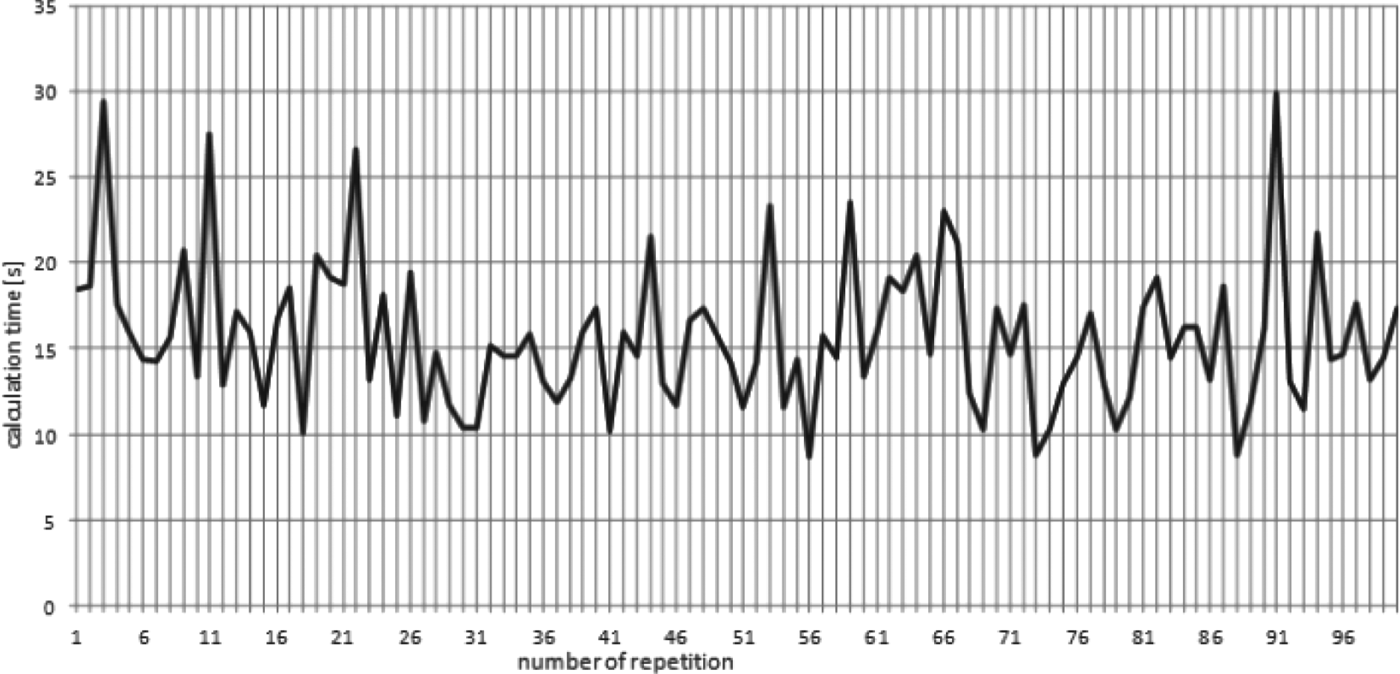
The calculations for this example situation have been repeated 100 times. The results obtained were identical for every repetition. The calculations differ only in computational time (presented by the graph in Figure 9). The shortest computational time was 8·64 seconds, while the longest computational time was 29·88 seconds, so it has never exceeded one minute. The value of the mean computational time for one hundred repetitions of calculations was 15·69 seconds.

Figure 9. Computational time for every repetition of calculation for example Scenario 1.

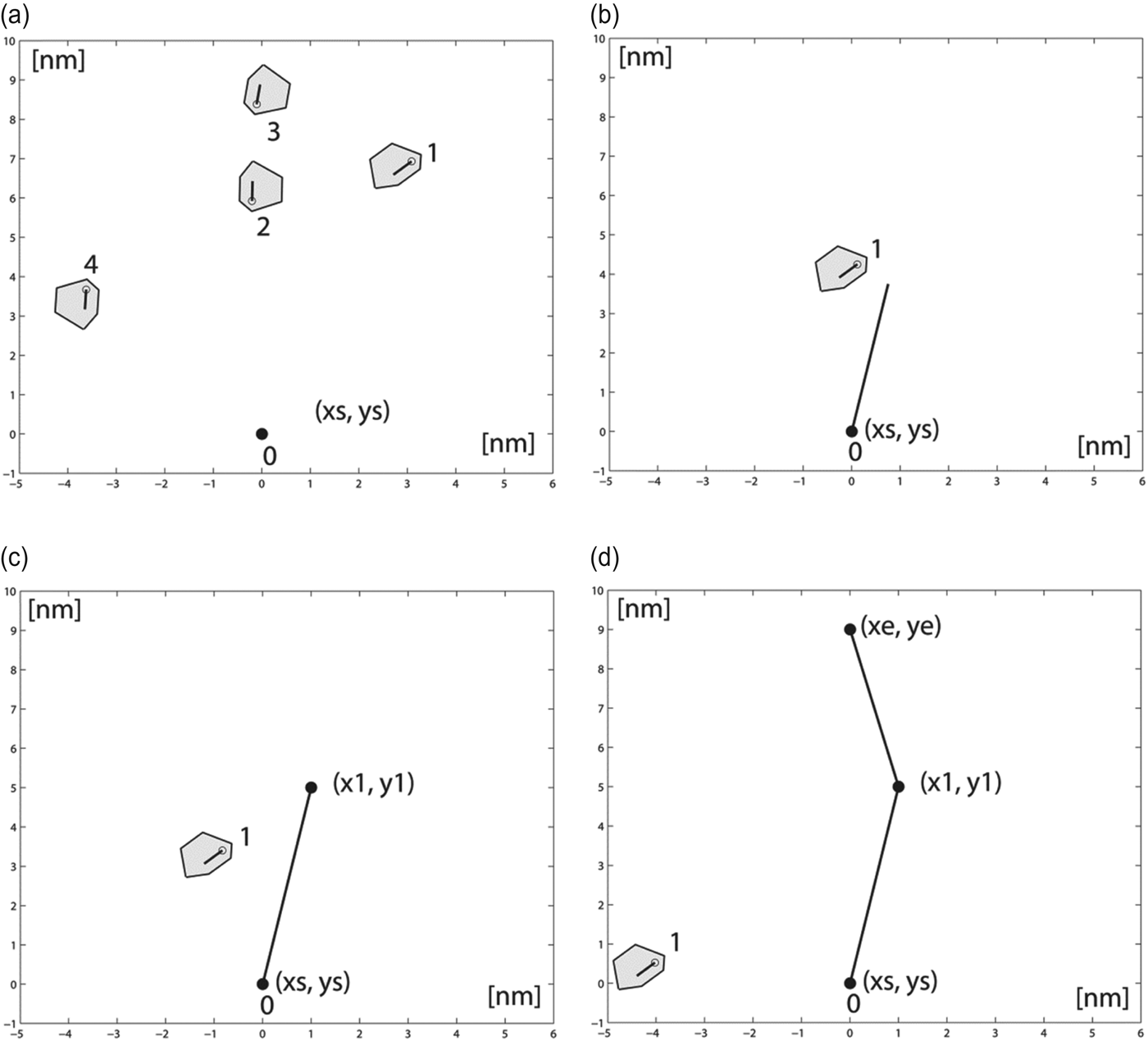
Figure 10 shows the successive stages of the own ship movement along the determined trajectory. Figure 10(a) presents the initial phase of the navigational situation. The figure is oriented in the own ship course up orientation; this means that the own ship heading line points upwards on the graph. In Figure 10(b) the closest approach of the target ship 1 with respect to the own ship is presented. Figure 10(c) presents the situation when the own ship is located at waypoint one (wp1(x1,y1)), after it has altered its course to 077°. Figure 10(d) shows the situation when the own ship reaches the ending waypoint (wpe(xe,ye)), after it has changed its course to 052°.

Figure 10. Graphical solution of Scenario 1.

The graphical presentation of results at consecutive stages of the own ship movement confirms that the calculated own ship manoeuvres allow the avoidance of all target ships, maintaining a safe distance between the ships. The values of course alterations were 11° to the starboard side and 25° to the port side, that proves that the solution fulfils Rule 8(b) of COLREGs. This rule states that “any alteration of course and/or speed to avoid collision shall, if the circumstances of the case admit, be large enough to be readily apparent to another vessel observing visually or by radar; a succession of small alterations of course and/or speed should be avoided”. The solution also satisfies Rule 15 of COLREGs. According to this rule “the vessel which has the other on her starboard side shall keep out of the way and shell, if the circumstances of the case admit, avoid crossing ahead of the other vessel”.

3.2. Scenario 2

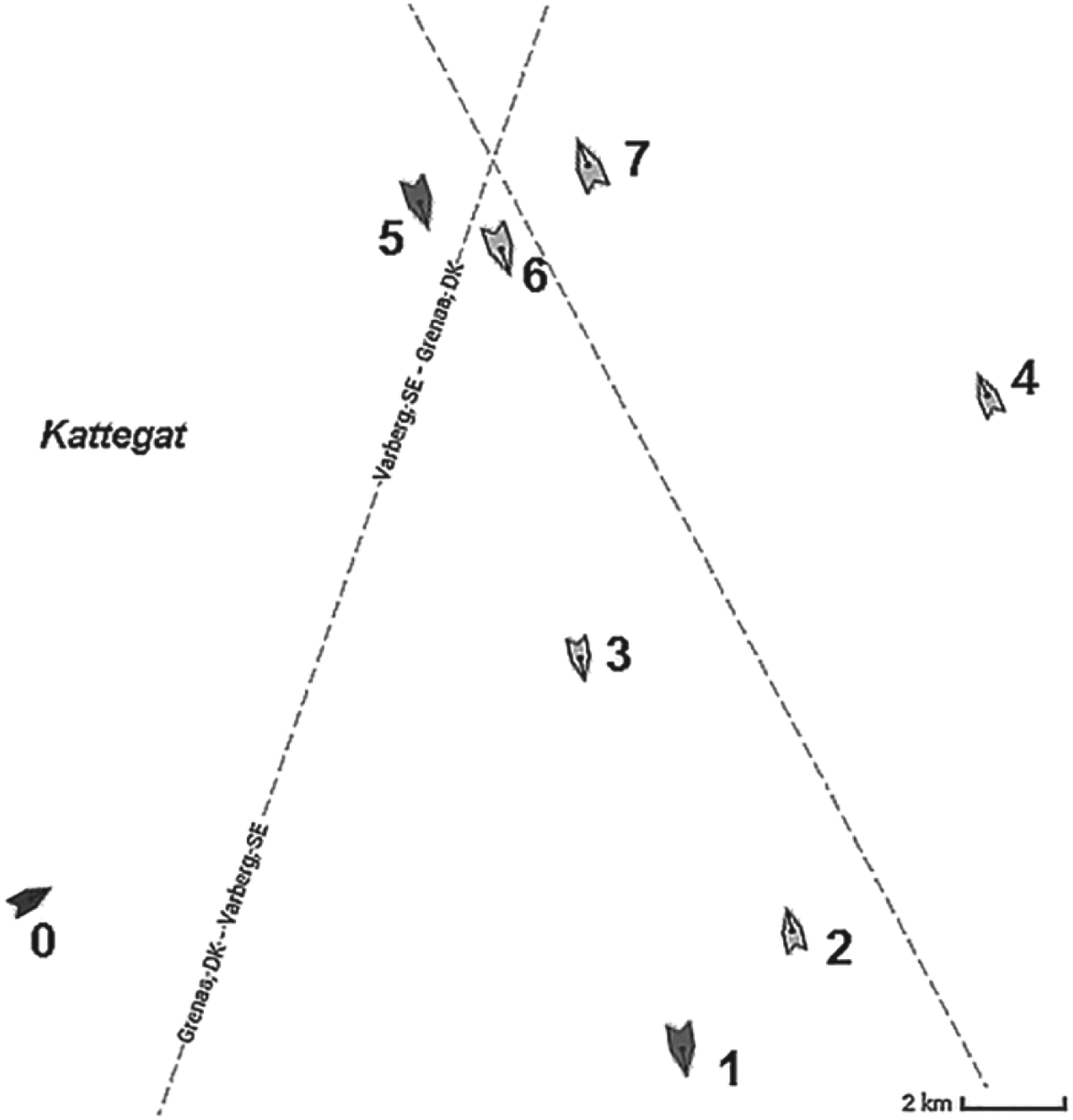
The second example navigational scenario presents an encounter situation of eight ships in the Kattegat area. The input data describing this situation are in Table 4, while Figure 11 shows the navigational situation registered by the Marine Traffic service.

Figure 11. Navigational Scenario 2 (source: http://www.marinetraffic.com/).

Table 4. Navigational data of Scenario 2.

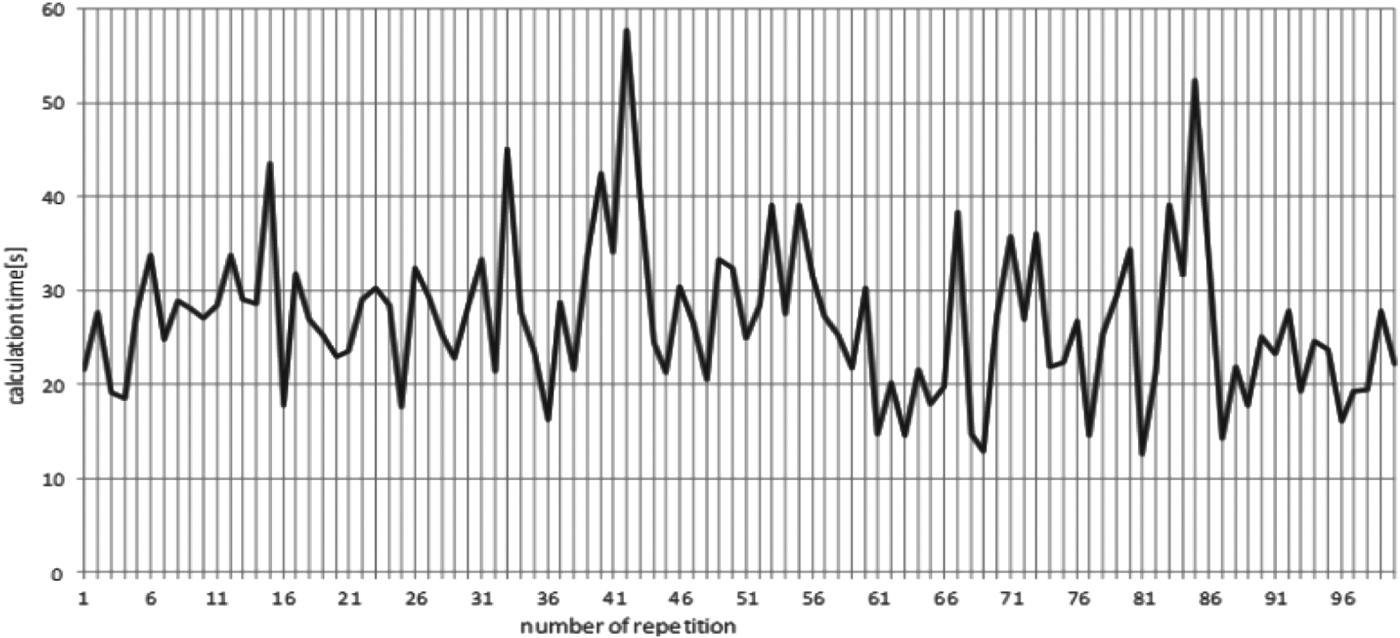
The calculations for this example were also repeated 100 times and the results obtained were also identical for every repetition. The differences in computational time between repetitions of calculations are presented in Figure 12. The shortest computational time was 12·59 seconds, while the longest computational time was 57·69 seconds, so it has never exceeded one minute. The value of the mean computational time for 100 repetitions of calculations was 26·93 seconds.

Figure 12. Computational time for every repetition of calculation for Scenario 2.

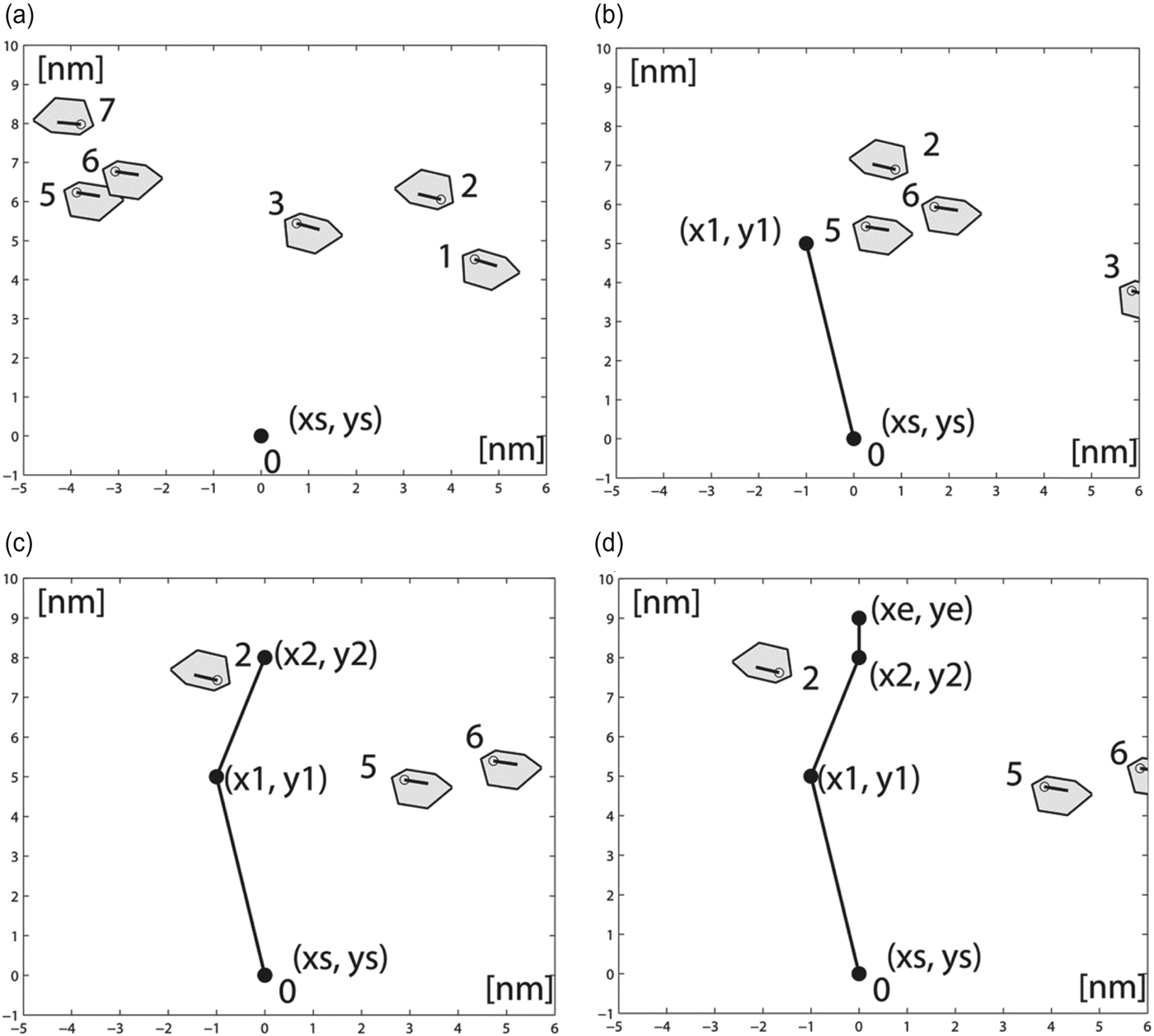
In Figure 13 the graphical solution of this example is presented. Figure 13(a) shows the initial phase of the situation. This situation is more complex than the previous one, but the algorithm has also dealt with finding a solution for this scenario by the determination of three manoeuvres. In Figure 13(b) the own ship is placed at waypoint one (wp1(x1,y1)), after it has changed its course to 050°. Figure 13(c) presents the situation when the own ship is placed in the waypoint two (wp2(x2,y2)), after it has altered its course to 079°. In Figure 13(d) the own ship is placed at the end waypoint (wpe(xe,ye)), after it has changed its course to 061°. The own ship course alterations have reached the following values: 11° to the port side, then 29° to the starboard side and finally 18° to the port side. These values confirm the solution's compliance with Rule 8(b) of COLREGs. The solution also fulfils Rule 15 of COLREGs.

Figure 13. Graphical solution of Scenario 2.

4. CONCLUSION

This paper presents a new approach to ship trajectory planning in collision situations at sea based on SI. The results presented confirm the successful implementation of the approach to solve the considered problem. The algorithm satisfactorily solves not only simple, but also complex situations, such as the example Scenario 2. The solutions meet the requirements of specific COLREGs, especially Rule 8(b), but also rules 14 and 15. The optimality of solutions is confirmed by the use of the objective function in the form of the smallest distance of the determined trajectory. It should also be mentioned that the objective function can be modified to include other factors such as the smallest turning angle of the own ship manoeuvre. The efficiency of the approach is confirmed by the results of simulation tests. It should be underlined that the results are identical for each of 100 repetitions and the computational time values vary from about ten to 60 seconds, which is acceptable for the implementation of such a method in on board collision avoidance systems. It can also be adapted to solve path-planning problems of mobile robots and manipulators.

To sum up, the following achievements of the approach have been distinguished:

• • implementation of the own ship dynamics in the form of the manoeuvre time

• • meeting the requirements of specific COLREGs

• • determination of the own ship trajectory to the specified final point, which enables the method to solve navigational situations in restricted waters

• • the ability to include the avoidance of static obstacles (e.g. land, shallows, buoys)

• • identical solutions for every repetition of calculations.

The following limitations have also been noted:

• • the speed reduction manoeuvre of the own ship has not been implemented

• • changes of the target ships' strategies are not considered, when the target ship course or speed change is detected, calculations have to be performed for this new navigational situation

• • computational time is different for every repetition of calculations

• • computational time could be shorter.

Further developments of the presented approach include the implementation of the algorithm in the C programming language, the implementation of the speed change manoeuvre of the own ship, when the solution of the own ship course alteration cannot be found and the introduction of parallel calculations, which will shorten the computational time.