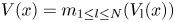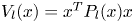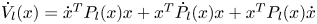Optimal design via polynomial Euler function for UAV applications

Abstract

Unmanned aerial vehicles (UAVs) have recently been widely applied in a comprehensive realm. By enhancing computer photography and artificial intelligence, UAVs can automatically discriminate against environmental objectives and detect events that occur in the real scene. The application of collaborative UAVs will offer diverse interpretations which support a multiperspective view of the scene. Due to the diverse interpretations of UAVs usually deviating, UAVs require a consensus interpretation for the scenario. This study presents an original consensus-based method to pilot multi-UAV systems for achieving consensus on their observation as well as constructing a group situation-based depiction of the scenario. Taylor series are used to describe the fuzzy nonlinear plant and derive the stability analysis using polynomial functions, which have the representations $V(x )={m_{\textrm{1} \le l \le N}}({{V_\textrm{l}}(x )} )$ and ${V_l}(x )={x^T}{P_l}(x )x$. Due to the fact that the ${\dot{P}_l}(x )$ in ${\dot{V}_l}(x )={\dot{x}^T}{P_l}(x )x + {x^T}{\dot{P}_l}(x )x + {x^T}{P_l}(x )\dot{x}$ will yield intricate terms to ensure a stability criterion, we aim to avoid these kinds of issues by proposing a polynomial homogeneous framework and using Euler's functions for homogeneous systems. First, this method permits each UAV to establish high-level conditions from the probed events via a fuzzy-based aggregation event. The evaluated consensus indicates how suitable is the scenario collective interpretation for every UAV perspective.

1. Introduction

Since the publication of the Takagi–Sugeno fuzzy model (Takagi and Sugeno, 1985; Dai et al., 2022, 2023; Zhang et al., 2023c, 2023d; Feng et al., 2024), there has been a link between the linear system and the nonlinear system. Through fuzzy theory, a nonlinear system that is difficult to analyse could be divided into a combination of multiple linear subsystems and their corresponding fuzzy rules, and then the stability of each fuzzy system can be analysed and its system performance calculated, including H ₂ and H_∞, so that the analysis of such nonlinear systems has a better solution. Generally, most scholars choose the Lyapunov function to analyse the stability of the system, and most of the literature focuses on the common Lyapunov function. This detection method is also called quadratic stability (Wu et al., 2022; Xu et al., 2022; Zheng et al., 2022), and other stability criteria have been developed so far to improve the conditions which could be more relaxed. Most of the stability analysis in early literature studies is solved by a parallel distributed compensation controller (PDC: parallel distributed compensation) and quadratic stability (Li et al., 2022a, 2022b, 2022c; Di et al., 2023; Zheng et al., 2023a). However, this method is too simple and conservative, so future research focuses on how to reduce its conservatism, which makes the solution more relaxed. To reduce the conservatism of the solution, non-parallel distributed compensation and non-common Lyapunov function are proposed by scholars; some studies are also performed by adding loose matrix or loose variables, or by introducing Pólya's theorem to add time-varying or non-time-varying parameters to reduce conservatism (Wang et al., 2022; Guo et al., 2023); even in recent years, some scholars have proposed different types of Lyapunov functions, such as the non-quadratic Lyapunov function (Bai et al., 2021; Sun et al., 2022; Shi et al., 2023a, 2023b; Yang et al., 2023, 2024; Zhang et al. 2023a) and piecewise quadratic Lyapunov function (Dai et al., 2022; Yang et al., 2023; Zhang et al., 2023b).

Among many research subjects, the piecewise continuous Lyapunov function is also a research topic widely concerned by scholars. The concept of piecewise analysis is added to the system to make the system stability analysis more relaxed (Li and Yao, 2023; Liu et al., 2024; Luo et al., 2023; Chen et al., 2024; Hou et al., 2023b). Later, other scholars added the controller design for analysis and verified the reason why only the minimum-type polynomial piecewise Lyapunov function can design the controller for the two types of Lyapunov functions (Zheng et al., 2023b). If the definition of the largest type piecewise Lyapunov function is used, the sufficient condition will be contrary to its definition. Some scholars would rather study the stable region of attraction (Sun et al., 2020, 2021, 2022; Wang et al., 2024a, 2024b). Furthermore, this paper mainly studies the non-quadratic stability of piecewise continuous Lyapunov functions, meaning a non-constant matrix P(x) that composes Lyapunov functions, and is also a type of non-common Lyapunov functions. In the study of a Lyapunov function above the third power, since it is necessary to discuss the differential rate $\dot{V}$ of the Lyapunov function V, most literature inevitably generated the differential term $\dot{P}$ of the Lyapunov matrix P (Wang et al., 2023) and this differential term will cause difficulties in the sufficient criterion. This paper thereby employs the Euler's polynomial theorem of an homogeneous function to solve this problem. Artificial neural networks (ANNs) have been shown to be potential means of problem solving due to their unique properties such as massively parallel processing, adaptive learning capabilities, self-organisation and robustness (Tian et al., 2022; Li and Yao, 2023; Tan et al., 2023; Wang et al., 2023; Zheng et al., 2023b). However, the main problem with ANNs is that these numbers hidden in neurons have a direct and strong effect on the neuron's performance. Therefore, we need to sacrifice the operation time to fulfil the efficiency and accuracy of the computations, which makes the NN tool hard to be used online or in real time for applications. Therefore, the traditional NN approaches, for example, a multilayer perceptron for varying time signals or systems, are not very suitable because of their static system structure. To handle this problem, fuzzy neural networks (FNNs) are considered as a flexible and reasonable alternative because they combine biologically inspired learning with human thinking mechanisms. Because the mechanism is adjusted by fuzzy and recurrent self-evolving schemes, the stability and performance could be improved and demonstrated in this paper. When combined with nonlinear activation functions, RNNs can handle complex spatiotemporal patterns. Therefore, this paper highlights an RSEFNN (recurrent self-evolving FNN) with local feedback to classify cognitive system states for those applications of UAVs.

This method generates significant beneficial results for multi-UAV systems for condition awareness, e.g. the reliability evaluation of consensus-based group decisions. For example, when a UAV team participated in a rescue mission, if their detecting results achieve a decision with a high degree of agreement, then the rescuers can regard the UAV team's interpreting scene as dependable. Otherwise, rescuers cannot trust the results of the UAV team. Thus, if the ultimate result can satisfy the scenario interpretations of the individual UAVs, the consensus evaluation is obviously significant.

Table 1 lists the abbreviations used in this work and the study is arranged as follows. Section 2 presents preliminary knowledge of the generalised dissimilarity modelling (GDM) procedures, such as consensus modelling and the fuzzy ontologies, and refers to the cognition of multi-UAV systems. Section 3 describes the study's method, and emphasises the UAV preference for generating in conditions and constructing the consensus-based decision-making model. Section 4 displays the operating principle of the study method in a scenario of a classic case. Finally, Section 5 dissertates the merits and inferiority of the provided approach in comparison to each of the other approaches, which also propose the conclusions of the paper.

Table 1. Abbreviation of full names

2. Preliminary theory for Euler homogeneous polynomials

To be able to deduce smoothly in the following sections, the preliminary theorems related to this paper will be introduced here.

Lemma 2.1. Congruent transformation. It is known that a matrix M is a positive definite matrix, and X is multiplied on its left and right sides, where X must be an ${X^T}$ matrix of full rank. After congruent transformation, the obtained matrix ${X^T}\textrm{MX}$ is also a positive definite matrix, its invariance remains unchanged before and after conversion, and vice versa.

\[M\mathrm{\ > }0 \Leftrightarrow {X^T}\textrm{MX} > 0\]

Lemma 2.2. Continuous Lyapunov asymptotic stability. For a continuous time-invariant system for $\dot{x}=f(x )$ and $f(0 )=0$, that is, the equilibrium point is at the origin, if there is a Lyapunov function $V(x )={x^T}Px$ satisfying the following constraint condition, the system is quadratic asymptotically stable and converges to an equilibrium point:

\begin{gather}V(x )\mathrm{\ > }0\nonumber\end{gather}

\begin{gather}\frac{{\partial V}}{{\partial x}}f(x )\mathrm{\ < }0\nonumber\end{gather}

Lemma 2.3. Schur complement. Suppose A, B, C, D are p × p, p × q, p × q and q × q matrices, respectively, and D is an invertible matrix. As shown below, we can convert this matrix inequality through the Shaw transformation technique into the form of linear matrix inequalities, and vice versa.

\[\left\{ {\begin{array}{@{}c} {A - B{D^{ - 1}}{C^T} < 0}\\ {D\mathrm{\ < }0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{@{}cc@{}} A& B\\ {{C^T}}& D \end{array}} \right]\mathrm{\ < }0\]

We then introduce the continuous system architecture and modelling method, the S-procedure, and extend it to the minimal form of homogeneous Lyapunov function. We then solve the differential term problem of P(x) with the help of Euler order theorem and finally prove the minimal stability test conditions for controller design of type-fragment homogeneous Lyapunov functions.

2.1 Continuous fuzzy system and fuzzy rules

This section is represented by a polynomial fuzzy system. We consider a nonlinear fuzzy system and convert it into r rules for description, which can be expressed as follows.

If ${\mathrm{\Omega }_1}$ is ${M_{i\textrm{1}}}$ and ${\mathrm{\Omega }_r}$ is ${M_{ir}}$,

(1)\begin{equation}\dot{x}(t )={A_i}(x )x(t )+ {B_i}(x )u(t ),\;i=1,2, \cdots ,r\end{equation}

where r is the number of fuzzy rules; ${M_{i1}}, \cdots ,{M_{ir}}$ is a fuzzy set; ${\mathrm{\Omega }_1}(t ), \cdots ,{\mathrm{\Omega }_p}(t )$ is a variable (premise variable) of the fuzzy rule; $x(t )={[{x_1}(t ),{x_2}(t ), \cdots ,{x_n}(t )]^T} \in {R^n}$ is a state vector; and $u(t )={[{u_1}(t ),{u_2}(t ), \cdots ,{u_m}(t )]^T} \in {R^m}$ is a control input vector.

Therefore, after standard fuzzy inference, defuzzification and normalisation, the following generalised polynomial fuzzy system can be used to describe the nonlinear system:

(2)\begin{align}\begin{aligned} \dot{x}(t )& =\mathop \sum \limits_{i = 1}^r {\mu _i}{A_i}(x )x(t ) + \mathop \sum \limits_{i = 1}^r {\mu _i}{B_i}(x )u(t )\\ & = {A_\mu }(x )x(t ) + {B_\mu }(x )u(t )\end{aligned}\end{align}

In this paper, the polynomial fuzzy feedback control matrix type is $u(t )={K_\mu }(x )x(t )$, where ${K_\mu }(x )$ is the control gain and $\mu \in {R^r}$ belongs to the set ${\Delta _r}$, and its definition is as follows:

(3)\begin{equation}{\Delta _r}=\left\{ {\mu \in {R^r}:\mathop \sum \limits_{i = 1}^r {\mu_i}=1,{\mu_i} \ge 0} \right\}\end{equation}

and Equation (3) can be understood as an r polyhedron structure formed by connecting points with line segments.

2.2 Euler homogeneous polynomials

Generally, when deriving non-quadratic stability conditions, the differentiation of the Lyapunov function with respect to time will generate the differential term $\dot{P}$ (x) of the Lyapunov matrix P(x) with respect to time, which makes the whole derivation process more complicated and cumbersome, so in this section, we will quote the characteristics of the Eurasian polynomial theorem to avoid this differential term, making the whole derivation process easier.

Lemma 2.4. The function $V(x )\textrm{:}{R^n} \to R$ is a homogeneous Lyapunov function of degree r, if and only if

(4)\begin{align}V({\lambda x} )={\lambda ^g}V(x )\end{align}

is satisfied, where $x \in {R^n}$, $\lambda \ge 0$.

Lemma 2.5. Euler's homogeneous relations (Sun et al., 2020, 2022; Wang et al., 2024a, 2024b). V (x) is an homogeneous polynomial of degree g if and only if the V (x) function satisfies

(5)\begin{align}\begin{aligned} gV(x )& = {x^T}{\nabla _x}V(x )\\ & = \left[ {\begin{array}{@{}cccc@{}} {{x_1}}& {{x_2}}& \cdots & {{x_n}} \end{array}} \right]\left[ {\begin{array}{@{}c@{}} {\dfrac{{\partial V}}{{\partial {x_1}}}}\\ {\dfrac{{\partial V}}{{\partial {x_2}}}}\\ \vdots \\ {\dfrac{{\partial V}}{{\partial {x_n}}}} \end{array}} \right]\\ & = \left[ {\begin{array}{@{}cccc@{}} {\dfrac{{\partial V}}{{\partial {x_1}}}}& {\dfrac{{\partial V}}{{\partial {x_2}}}}& \cdots & {\dfrac{{\partial V}}{{\partial {x_n}}}} \end{array}} \right]\left[ {\begin{array}{@{}c@{}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right]\\ & = {\nabla _x}V{(x)^T}x \end{aligned}\end{align}

Partially differentiating the above formula with respect to x gives

(6)\begin{equation}g{\nabla _x}V(x )={\nabla _x}V(x )+ {\nabla _{xx}}V(x )x\end{equation}

The relationship between gradient and Hessian matrix can be obtained after transposition:

(7)\begin{equation}{\nabla _x}V(x )=\frac{1}{{g - 1}}{\nabla _{xx}}V(x )x\end{equation}

2.3 S-procedure

In this section, we will introduce the S-procedure (Li and Yao, 2023) to understand the meaning of adding parameter λ_s by citing the following lemma.

Lemma 2.5. S-procedure. Assume ${F_0}(x )$, ${F_1}(x )$ to be two arbitrary quadratic functions in the space, ${R^n}$, and for all $x \in {R^n}$, ${F_1}(x )< 0$ and ${F_0}(x )< 0$ if and only if there exists a $\tau \ge 0$ causing

(8)\begin{equation}{F_0}(x )- \tau {F_1}(x )\le 0\end{equation}

The symbol transformation of the above formula will be understood as the following inequality:

(9)\begin{equation}{F_0}(x ) + \tau {F_1}(x )\le 0\end{equation}

Equation (9) holds if and only if ${F_0}(x )< 0$ and ${F_1}(x )\ge 0$.

We will use this method to rewrite the Lyapunov function as the minimal form fragment Lyapunov function to be presented, and in terms of computer simulations, we will try to find suitable values for τ.

2.4 Minimal form fragment Lyapunov function

This section will introduce the minimum-type polynomial piecewise Lyapunov function (Zheng et al., 2023b) and explain why only the minimum-type polynomial piecewise Lyapunov function is used for controller design.

Lemma 2.6. Minimum-type polynomial piecewise Lyapunov function.

Defining a minimal form fragment Lyapunov function

\[V(x )={m_{\textrm{1} \le l \le N}}({{V_l}(x )} ){V_l}(x )={x^T}{P_l}x\]

where N is the piecewise number of Lyapunov function, $l=1 \cdots ,N$, and the minimal form piecewise Lyapunov function has to be

1. (1) $V({x({{t^ + }} )} )\le {V_l}({x({{t^ + }} )} )$,

2. (2) $\dot{V}({x({{t^ + }} )} )\le {\dot{V}_l}({x({{t^ + }} )} )\textrm{\; }$,

and $V({x(t )} )={V_l}({x(t )} )$, then

\[V({x({{t^ + }} )} )- V({x(t )} )\le {V_l}({x({{t^ + }} )} ){V_l}({x(t )} )\]

Take the limit at the same time

\[\mathop {\textrm{lim}}\limits_{{t^ + } - t \to 0} \frac{{V({x({{t^ + }} )} )- V({x(t )} )}}{{{t^ + } - t}} \le \mathop {\textrm{lim}}\limits_{{t^ + } - t \to 0} \frac{{{V_l}({x({{t^ + }} )} ){V_l}({x(t )} )}}{{{t^ + } - t}}\]

\[\dot{V}({x({{t^ + }} )} )\le {\dot{V}_l}({x({{t^ + }} )} )\textrm{\; }\]

Therefore, ${\dot{V}_l}(x )< 0$ guaranteed $\dot{V}(x )< 0$, so if the maximum type Lyapunov function is selected, its characteristic under $V({x({{t^ + }} )} )\ge {V_l}({x({{t^ + }} )} )$ cannot guarantee $\dot{V}(x )< 0$; therefore, it is not selected and another reason will be explained in the main theorem.

For the convenience and understanding of subsequent proofs, the controlled system considered in the reference is changed to a polynomial form, and the Lyapunov function P is also changed to a polynomial form P(x) which is divided into N segments to be ${P_l}(x )$. The controller is similarly changed to ${u_l}(t )={K_{\mu l}}(x )x(t )$, and according to the system in Equation (2), $u(t )={u_l}(t )$, the following continuous closed-loop fuzzy system can be described:

(10)\begin{equation}\dot{x}={A_\mu }(x )x(t ) + {B_\mu }(x ){u_l}(t )\end{equation}

Substituting the controller ${u_l}(t )={K_{\mu l}}(x )x(t )$ into Equation (10), then we get

(11)\begin{equation}\dot{x}=({{A_\mu }(x ) + {B_\mu }(x ){K_{\mu l}}(x )} )x\end{equation}

Equation (11) can be understood as the controlled body is not piecewise, but the control force is piecewise, and thus

\[{\bar{A}_{\mu \mu l}}={A_\mu }(x ) + {B_\mu }(x ){K_{\mu l}}(x )\]

Here it is shown that the system is a polynomial Lyapunov function with a stability condition of

(12)\begin{equation}{\bar{A}_{\mu \mu l}}{(x)^T}{P_l}(x ) + {P_l}(x ){\bar{A}_{\mu \mu l}}(x )< 0\end{equation}

Using the concept of the S-procedure, Equation (12) is designed into the following inequality:

(13)\begin{equation}{\bar{A}_{\mu \mu l}}{(x)^T}{P_l}(x )+ {P_l}(x ){\bar{A}_{\mu \mu l}}(x )+ \mathop \sum \limits_{s = 1}^N {\lambda _s}({{P_s}(x )- {P_l}(x )} )< 0\end{equation}

where ${\lambda _s}$ > 0, so it can correspond to τ of the S-procedure.

The purpose of applying this method is to stabilise the original Lyapunov function in Equation (12), according to the S-procedure, through adding ${\lambda _s}({{P_l}(x )- {P_s}(x )} )$, which helps to guarantee that ${\bar{A}_{\mu \mu l}}{(x)^T}{P_l}(x )+ {P_l}(x ){\bar{A}_{\mu \mu l}}(x )$ is less than zero. The criterion can be used and then can be solved through subsequent simplification, which will be clarified in the following subsection.

2.5 Stability conditions for controller design of minimised fragmentary homogeneous Lyapunov functions

In addition to the goal of making the system stable, the existing method of stabilising the system (the original Lyapunov function) is not sufficient. To increase the stability, the controller is designed to stabilise the system using the minimal form of the fragment homogeneous polynomial Lyapunov function of the fuzzy system analysis, and through the method of homogeneous polynomials, we can simplify the solution process.

Theorem 2.1. According to the continuous fuzzy system in Equation (11), we will design the controller to stabilise the system through the minimal form of the fragment homogeneous Lyapunov function, assuming a Lyapunov function V (x) is a homogeneous polynomial with degree g. There is an homogeneous positive definite symmetric matrix $Q(x )=Q{(x)^T} \in {R^{n \times n}}$, ${Q_\textrm{l}}(x )=P_l^{ - 1}(x )$) and an asymmetric matrix F(x), satisfying the following inequalities:

\begin{align}& {Q_l}(x )> 0\nonumber\end{align}

\begin{align}& {M_{iil}}(x )> 0\;i=1,2, \cdots ,r\nonumber\end{align}

\begin{align}& {M_{ijl}}(x ) + {M_{jil}}(x )> 0\;i=1,2, \cdots ,r - 1;j=i + 1, \cdots ,r\nonumber\end{align}

where $l=1,2, \cdots ,N$, N is the number of Lyapunov function segments,

\begin{gather}V(x )= {m_{1 \le l \le N}}({{V_l}(x )} )\nonumber\end{gather}

\begin{gather}{V_l}(x )= {x^T}{P_l}(x )x\nonumber\end{gather}

\begin{gather}{M_{iil}}(x )= \left[ {\begin{array}{*{20}{c}} {{N_{iil}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]\nonumber\end{gather}

\begin{gather}{N_{ill}}(x )={Q_l}(x ){A_i}{(x)^T}(x )+ F_{il}^T(x ){B_i}{(x)^T}(x )+ \mathrm{\ \star } - \mathop \sum \limits_{s = 1}^N {\lambda _s}{Q_l}(x )\nonumber\end{gather}

\begin{gather}{M_{ijl}}(x )=\left[ {\begin{array}{*{20}{c}} {{N_{ijl}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_\textrm{1}}{Q_\textrm{1}}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]\nonumber\end{gather}

\begin{gather}\begin{array}{*{20}{c}} {{M_{jil}}(x )}& { = \left[ {\begin{array}{*{20}{c}} {{N_{jil}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]} \end{array}\nonumber\end{gather}

\begin{gather}{N_{ijl}}(x )={Q_l}(x ){A_i}{(x)^T}(x ) + F_{jl}^T(x ){B_i}{(x)^T}(x )+ \mathrm{\ \star } - \sum\limits_{s = 1}^N {{\lambda _s}{Q_l}(x )}\nonumber\end{gather}

\begin{gather}{N_{jil}}(x )={Q_l}(x ){A_j}{(x)^T}(x ) + F_{il}^T(x ){B_j}{(x)^T}(x )+ \mathrm{\ \star } - \sum\limits_{s = 1}^N {{\lambda _s}{Q_l}(x )}\nonumber\end{gather}

\begin{gather}{F_{il}}(x )={K_{il}}(x ){Q_l}(x )\nonumber\end{gather}

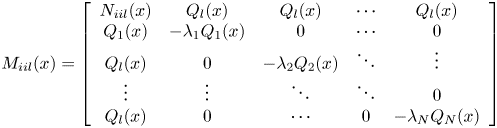
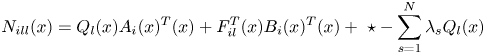
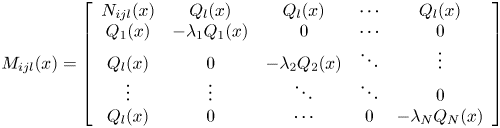
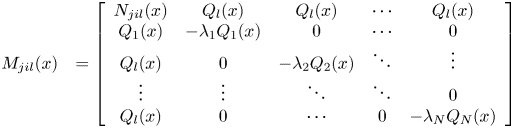
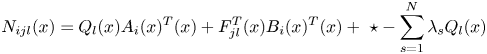
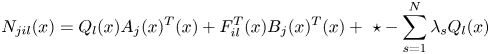
Proof According to the Lyapunov theorem to analyse the continuous fuzzy closed-loop control system in Equation (11), we assume that ${Q_l}(x )=P_l^{ - 1}(x )$ and the sub-g piecewise homogeneous Lyapunov function is as follows:

(14)\begin{equation}{V_l}(x )={x^T}{P_l}(x )x\mathrm{\ > }0,\;l=1, \ldots ,N\end{equation}

According to the Euler homogeneous relations in Equation (7), its differential formula can be obtained:

(15)\begin{equation}{\dot{V}_l}(x )=g{\dot{x}^T}{P_l}(x )x\end{equation}

Based on ${\dot{x}^T}={x^T}\bar{A}_{\mu \mu l}^T(x )$, then

(16)\begin{equation}{\dot{V}_l}(x )=g{x^T}\bar{A}_{\mu \mu l}^T(x ){P_l}(x )x\end{equation}

Then dividing g by 2, the following formula can be shown with $\bar{A}_{\mu \mu l}^T(x ){P_l}(x )$:

(17)\begin{equation}{\dot{V}_l}(x )=\frac{g}{2}{x^T}({\bar{A}_{\mu \mu l}^T(x ){P_l}(x ) + {P_l}(x ){{\bar{A}}_{\mu \mu l}}(x )} )x\end{equation}

To make the system asymptotically stable, it is necessary for ${\dot{V}_l}(x )< 0$ that

(18)\begin{equation}\frac{g}{2}{x^T}({\bar{A}_{\mu \mu l}^T(x ){P_l}(x ) + {P_l}(x ){{\bar{A}}_{\mu \mu l}}(x )} )x < 0\end{equation}

Finally, the normal constants are divided and through the congruent conversion,

(19)\begin{equation}\bar{A}_{\mu \mu l}^T(x ){P_l}(x )+ {P_l}(x ){\bar{A}_{\mu \mu l}}(x )< 0\end{equation}

Taking in $\sum\nolimits_{s = 1}^N {{\lambda _s}({{P_\textrm{s}}(x )- {P_l}(x )} )}$ items according to the S-procedure, we then have

(20)\begin{equation}\bar{A}_{\mu \mu l}^T(x ){P_l}(x )+ {P_l}(x ){\bar{A}_{\mu \mu l}}(x )+ \mathop \sum \limits_{s = 1}^N {\lambda _s}({{P_s}(x )- {P_l}(x )} )\mathrm{\ < }0\end{equation}

Multiply the inequality left and right by ${Q_l}(x )$:

(21)\begin{equation}{Q_l}(x )\bar{A}_{\mu \mu l}^T(x )+ {\bar{A}_{\mu \mu l}}(x ){Q_l}(x ) + \mathop \sum \limits_{s = 1}^N {\lambda _s}({Q_l}(x ){P_s}(x ){Q_l}(x )- {Q_l}(x )\mathrm{\ < }0\end{equation}

After Shur complement and order ${N_{\mu \mu l}}={Q_l}(x )\bar{A}_{\mu \mu l}^T(x ) + {\bar{A}_{\mu \mu l}}(x ){Q_l}(x )$, we can get

(22)\begin{equation}\left[ {\begin{array}{*{20}{c}} {{N_{\mu \mu l}}}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right] < 0\end{equation}

where $l=1, \cdots ,N$, and taking the sub-matrix ${N_{\mu \mu l}}$ of Equation (22),

\[{Q_l}(x )\bar{A}_{\mu \mu l}^T(x ) + {\bar{A}_{\mu \mu l}}(x ){Q_l}(x )- \mathop \sum \limits_{s = 1}^N {\lambda _s}{Q_l}(x )\mathrm{\ < }0\]

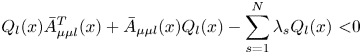
Substitute the state matrix ${\bar{A}_{\mu \mu l}}(x )={A_\mu }(x )+ {B_\mu }(x ){K_{\mu l}}(x )$ back into

\[{Q_l}(x ){({{A_\mu }(x ) + {B_\mu }(x ){K_{\mu l}}(x )} )^T} + \mathrm{\ \star } - \mathop \sum \limits_{s = 1}^N {\lambda _s}{Q_l}(x )\mathrm{\ < }0\]

Suppose a new variable ${F_{\mu l}}(x )={K_{\mu l}}(x ){Q_l}(x )$ to replace the double variables

\[{Q_l}(x ){A_\mu }{(x)^T}x + F_{\mu l}^T(x ){B_\mu }{(x)^T}x + \mathrm{\ \star } - \mathop \sum \limits^N {\lambda _s}{Q_l}(x )\mathrm{\ < }0\]

By means of Equations (25) and (22), the system stability analysis can be carried out.

The second reason for using the minimal form fragment Lyapunov function is explained here. If the maximal form fragment Lyapunov function is used, because the conditional inequality is ${Q_l}(x )\bar{A}_{\mu \mu l}^T(x ) + 16{\bar{A}_{\mu \mu l}}(x ){Q_l}(x )+ \sum\nolimits_{s=1}^N {{\lambda _s}({{P_l}(x )- {P_s}(x )} )\mathrm{\ > }0}$, it is proved by Equation (22) that the diagonal term will become ${\lambda _1}{Q_1}(x ), \cdots ,{\lambda _N}{Q_1}(x )$, then Equation (22), by turning back the Shur complement, will be found to violates the S-procedure, where λ <  0 is never found, so it is not applicable.

3. UAV practice in operations

Apply various types of UAVs to patrol a district and probe events coming from the scene of observation. Every UAV has been equipped with a technical background to complete a detection event (UAVs event detection team). UAVs could specifically probe mobile targets on the scene via tracking video algorithms, and also use scene ontology with contextual knowledge to fuse this information (Yin et al., 2022; Li and Zakarya, 2022; Liu et al., 2023; Hou et al., 2023a; Guo et al., 2023).

For modelling the UAV's probed events and its values of frequency, we expanded Track Stick ontology to a fuzzy ontology. All types of UAV probed events as well as their valuable frequency are appended to the system ontology as principles. The applied principle is expressed as the triple $\left\langle e \right.,u, f \rangle$, whereas e the event type, u is the UAV entity, and f the event type's valuable frequency. The principle indicates that this UAV u probed the event type e with the valuable frequency f.

According to the frequency value of event types, the event descriptor describing event types is modelled as the concept in fuzzy ontology. Figure 1 displays three descriptors' event definitions of a specific event e: Low E, Medium E, High E. That is, the event e is a model of variable linguistic (fuzzy linguistic) terms in the three fuzzy concepts depicted by the membership functions which are fuzzy of the figure. These three conceptions depict different densities of vehicles (or people) related to the kind of event e in the specified scene. Depending on the valuable frequency, the descriptor events describe the participations in the type of event in detail in the form of the membership value which is fuzzy. For example, if the valuable frequency of e is low, low E can depict someone's participation in this event type more than Medium E and High E.

Figure 1. Descriptors in the e event

As soon as every UAV conveys preferences in conditions, the module M2 first permits UAVs to establish a decision in a group, so evaluates team agreements as well as probes which UAVs dominate the decision through using consensus reaching processes. Condition understanding based on a multi-UAV system is founded as a problem of GDM (Jiang et al., 2021; Chen et al., 2022a; Ma and Hu, 2022; Dai et al., 2023; Guo and Hu, 2023; Xiao et al., 2023); these conditions have been regarded as the alternatives, and every UAV in the system team can be evaluated as one expert. So, every UAV represents its preferences for these detected conditions (refer to Section 3A), officially, defining n UAVs as well as m conditions, every UAV conveys preferences in the m conditions. These preferences represented through the ith UAV are expressed in vector ${P^i}=(x_1^i,x_2^i, \ldots ,x_m^i)$, whereas ${P^i} \in {R^m},\forall i = 1,2, \ldots ,n$. This preference $x_j^i$, by the vector preference Pⁱ, expressed that the quantity of the ith UAV prefers some jth condition over any others. The number of dimensionality of preference vectors equals the number of stars used for the ranking system. The document preference vector is represented based on the average vector of term preference vectors.

As these UAV systems could comprise various kinds of UAVs (e.g. aerial, ground, sensor-based, etc.), every UAV possesses distinct functions and abilities. Further, the weather, e.g. luminosity and humidity, or any other environmental characteristics (that is, dense forests, radioactive regions), may decrease the capabilities of some UAVs. Therefore, each UAV has a reliability level; more specifically, w_i means the reliability weight incorporated with the ith UAV. For example, let us premeditate that a UAV team comprises three UAVs (i.e. UAV#1, UAV#2, and UAV#3), in which UAV#1 and UAV#3 have been equipped with action cameras and UAV#2 equipped with infrared cameras.

This kind of model summarises UAV preferences and defines the collective vector preference about this condition. The collective vector preference $\textrm{cp = (c}{\textrm{p}_1},\textrm{c}{\textrm{p}_2}, \ldots ,\textrm{c}{\textrm{p}_m})$ comprises m components, in which the jth factor ($\textrm{c}{\textrm{p}_j}$) presents this team's preference for this jth case. Hence, we let ${w_i}$ and ${P^i}=(x_1^i,x_2^i, \ldots ,x_m^i)$ be respectively that weight as well as vector preference which are incorporated with this ith UAV. The $\textrm{c}{\textrm{p}_j}$terms are given, while the arithmetic weighted mean in this UAV preferences in this jth case

(23)\begin{equation}\textrm{c}{\textrm{p}_j} = \frac{{\sum\nolimits_{i = 1}^n {(x_J^i \cdot {\omega _i})} }}{{\sum\nolimits_{k = 1}^n {{\omega _k}} }}\end{equation}

where the $\textrm{c}{\textrm{p}_j}$ value presents this global aggregation preference values in the jth condition, and $j = 1,2, \ldots ,m$. While given θ similarity vectors, n UAVs are evaluated, whereas $\theta =n \cdot (n - 1)/2$. Assuming ${P^j}$ and ${P^i}$ are the vector preferences for the jth and ith UAVs, respectively, the vector similarity $\textrm{S}{\textrm{V}^k}$ amid the UAV pair are computed as these distances between the UAVs vectors preference (Ma et al., 2023b; Song et al., 2022; Wang et al., 2022; Guo et al., 2023; Mi et al., 2023):

(24)\begin{equation}\textrm{S}{\textrm{V}^k}=|{ {{P^i} - {P^j}} |} \end{equation}

where $i \ne j$ and $k=1,2, \ldots ,i,\,\theta \,j=1,2, \ldots ,n$.

Level 2, A Consensus in situations (CS). By integrating a resemblance vector between the UAV pairs, the degree of consensus amid all the UAVs for each condition (CS) is acquired. Given the resemblance vector $\textrm{S}{\textrm{V}^k}\textrm{ = (SV}_1^k,\textrm{SV}_2^k,\textrm{SV}_m^k)$ amid the vectors preferences ${P^i}$ and ${P^j}$ in which $i \ne j$ and $i,j=1,2, \ldots ,n$, the degree of consensus $\textrm{c}{\textrm{s}_j}$ amid all of the UAVs on that jth condition has been computed as the average power mean of that jth element in all of the resemblance vectors:

(25)\begin{equation}\textrm{c}{\textrm{s}_j}={\left( {\frac{1}{t}\sum\limits_{k = 1}^t {{{|{ {\textrm{sv}_j^k} |} }^p}} } \right)^{1/p}}\end{equation}

where $j = 1,2, \ldots ,m$, and p the $p - \textrm{norm}$ average power value.

The degree of CS determines in what kind of conditions the UAVs exhibit divergence, thence, discriminate whether the team's decision is reliable on each condition. CS degree under all of the conditions (cr) has been computed as the average power means of the CS degree,

(26)\begin{equation}\textrm{cr = }\left( {\frac{{\sum\nolimits_{J = 1}^m {|{{{ {\textrm{c}{\textrm{s}_j}} |}^P}} } }}{m}} \right)\end{equation}

CS on the relation (cr) offers an unparalleled accumulative gauge for assessing the consistency amid UAVs in this team under all of the conditions. The denser cr is to zero, the higher the consistency of UAV under all the conditions, and the higher the reliability of the last decision group (ccp). The collective cumulative preference (ccp) is computed as these arithmetic means in the factors of these collective preferences.

(27)\begin{equation}\textrm{ccp = }\frac{{\sum\nolimits_{{J^2}=1}^m {\textrm{c}{\textrm{p}_j}} }}{n}\end{equation}

Once the vector preference ${P^i}=(x_1^i,x_2^i, \ldots x_m^i)$ for that ith UAV, the collective preference for that ith UAV amid all of the conditions is the arithmetic mean of its factors

(28)\begin{equation}\textrm{cu}{\textrm{v}^i} = \frac{1}{m}\sum\limits_{j = 1}^m {x_j^i}\end{equation}

where $i = 1,2, \ldots ,n$. The proximity and consensus degrees have been applied to explain the axioms of conditions and UAVs (Lu and Osorio, 2018; Cao et al., 2021; Lyu et al., 2023; Ma et al., 2023a; Qu et al., 2023a, 2023b). Thereby, the system can probe the most reasonable conditions and UAVs guiding the team's decision through requests.

According to Theorem 2.1, the inequality of the detection conditions of stability analysis can be tested by the method of sum of squares, so if the theorem condition is true, Theorem 2.1 is true, and the test rules are as follows:

${v^T}({{Q_l}(x )- {\mathrm{\epsilon }_1}(x )I} )v$ are SOS

$- {v^T}({{M_{ill}}(x ) + {\mathrm{\epsilon }_2}(x )I} )v$ are SOS $i=1,2, \cdots ,r$

$- {v^T}({{M_{ijl}}(x ) + {M_{jil}}(x )+ {\mathrm{\epsilon }_3}(x )I} )v$ are SOS $i=1,2, \cdots ,r - 1;j=i + 1, \cdots r$

where $v \in {R^n}$, ${\mathrm{\epsilon }_1}(x )> 0$, ${\mathrm{\epsilon }_3}(x )> 0$, $l=1, \cdots ,N$, N is the number of Lyapunov function segments

\begin{gather}V(x )={m_{1 \le l \le N}}({{V_\textrm{l}}(x )} )\nonumber\end{gather}

\begin{gather}{V_l}(x )={x^T}{P_l}(x )x\nonumber\end{gather}

\begin{gather}{M_{ijl}}(x )=\left[ {\begin{array}{*{20}{c}} {{N_{iil}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]\nonumber\end{gather}

\begin{gather}{N_{ill}}(x )={Q_l}(x ){A_i}{(x)^T}(x ) + F_{il}^T(x ){B_i}{(x)^T}(x ) + \mathrm{\ \star } - \mathop \sum \limits_{s=1}^N {\lambda _s}{Q_l}(x )\nonumber\end{gather}

\begin{gather}{M_{ijl}}(x )=\left[ {\begin{array}{*{20}{c}} {{N_{ijl}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_\textrm{1}}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(x )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]\nonumber\end{gather}

\begin{gather}{M_{jil}}(x )=\left[ {\begin{array}{*{20}{c}} {{N_{jl}}(x )}& {{Q_l}(x )}& {{Q_l}(x )}& \cdots & {{Q_l}(x )}\\ {{Q_1}(x )}& { - {\lambda_1}{Q_1}(x )}& 0& \cdots & 0\\ {{Q_l}(x )}& 0& { - {\lambda_2}{Q_2}(\textrm{x} )}& \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & 0\\ {{Q_l}(x )}& 0& \cdots & 0& { - {\lambda_N}{Q_N}(x )} \end{array}} \right]\nonumber\end{gather}

\begin{gather}{N_{ijl}}(x )={Q_l}(x ){A_i}{(x)^T}(x )+ F_{jl}^T(x ){B_i}{(x)^T}(x ) + \mathrm{\ \star } - \mathop \sum \limits_{s = 1}^N {\lambda _s}{Q_l}(x )\nonumber\end{gather}

\begin{gather}{N_{jil}}(x )={Q_l}(x ){A_j}{(x)^T}(x ) + F_{il}^T(x ){B_j}{(x)^T}(x ) + \mathrm{\ \star } - \mathop \sum \limits_{s = 1}^N {\lambda _s}{Q_l}(x )\nonumber\end{gather}

\begin{gather}{F_{il}}(x )={K_i}(x ){Q_l}(x )\nonumber\end{gather}

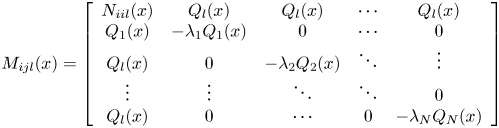
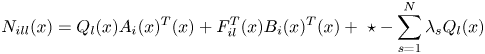
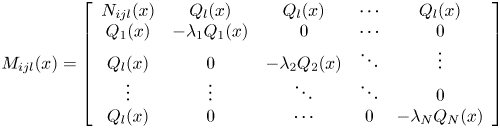
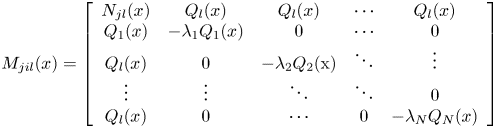
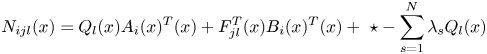
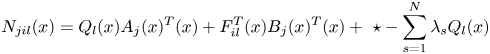
where v is an arbitrary parameter vector ${\varepsilon _1}(x )$ independent of x, ${\varepsilon _2}(x )$, ${\varepsilon _3}(x )$ are extremely small values and they can also be functions of x to exclude the possibility of SOS being 0.

The simulation of the example will be based on the theory in Section 2, and the computer simulation will be performed by using the sum of squares detection conditions in Section 3, where λ is the experimental value. According to the S-procedure, there exists a λ > 0 to ensure Equation (15) is established. As for the value of λ, each time for optimal selection is random numbers that are close to each other. In addition, the design method of Lyapunov matrix and control gain matrix in computer simulation is based on the method of Lu and Osorio (2018).

4. Numerical case

A case study is in the section to demonstrate how our model acts in the practical scene. Let us premeditate the experimental scene displayed in Figure 2. This scene relates to some people crossing as well as others walking nearby the road. Hence, let us presume a group of six UAVs achieved a site, spying on this district, in which the scenario demonstrated has been occurring. Every UAV could simultaneously probe five people at the scene via tracking video, where other moving objects have been filtered off (as shown by obj_6 in the figure). The UAV infers the constructed epistemology to probe events as the system ontology axioms (that is, predicate-object-subject triples), in which these event types (predicate) have been involved in the relevant personnel (subject) as well as the position where this event takes place (object). Taking an example, these axioms depict events detected via UAV#1 relating to probed people and POIs (Chen et al., 2022b, 2022c; Li et al., 2022c; Chen et al., 2023; Ma et al., 2023b; Yin et al., 2023).

Figure 2. Experimental study illustrating six UAVS observations and a practical scenario interpretation

Depending on Section 3, the module M1 implements an initial step which is identified by 0 for UAV configuration preferences, so the module M2 guides the UAVs to the last interpretation group via other steps. The flow chart is explained in Figure 3.

Figure 3. Flow chart of the UAV application with optimal design

4.1 Situation and preference generation

Calculate the frequencies which were related to each event's type probed by the UAVs. At this time, based on the query-based maximum concept satisfiability, it is probable to calculate this preference of UAV#1 on the marching people states. Generally, the preference of the UAV for a certain condition is produced by requesting the maximum satisfiability concept of UAV instance as well as their event type frequencies.

There are five statuses that can be recognised in this scene, displayed as Figure 2, such as simple crossing, people marching, traffic, shopping and men working on the road. UAVs will produce the preference values on these statuses, their results reported as Table 2. Due to the scene not showing any status which may affect any UAV's performances, for the purpose of simplification, by allocating its weights to one that supposes each UAV has the same reliability. Table 3 demonstrates the cps vectors. UAV#5 guides team decisions in all statuses and UAV#2 and UAV#4 represent the decisions most distinct from the ultimate team decision.

\begin{gather}\textrm{Rule}i\; \textrm{: IF}{\textrm{x}_1}(t )\,\textrm{is}\,{\textrm{M}_{i1}}\nonumber\end{gather}

\begin{gather}\textrm{Then}\,\dot{x}(t )={A_i}x + {B_i}u,\,i \in 1,2,3\nonumber\end{gather}

Table 2. Six UAVs preferences on five situations: men on the road (WRK); simple crossing (CRS); traffic (TRF); people marching (MAR); shopping (SHO)

Table 3. UAV cumulative proximity: each row illustrates a drone decision distinct from a decision by the group in all situations

Its constant system matrix is as follows:

\begin{gather}{A_1} = \left[ {\begin{array}{@{}cc@{}} {1.59}& { - 7.29}\\ {0.01}& 0 \end{array}} \right],{A_2} = \left[ {\begin{array}{@{}cc@{}} {0.02}& { - 4.64}\\ {0.35}& {0.21} \end{array}} \right],{A_3} = \left[ {\begin{array}{@{}cc@{}} { - \textrm{a}}& { - 4.33}\\ 0& {0.05} \end{array}} \right]\nonumber\end{gather}

\begin{gather}{B_1}=\left[ {\begin{array}{@{}c@{}} 1\\ 0 \end{array}} \right],{B_2}=\left[ {\begin{array}{@{}c@{}} 8\\ 0 \end{array}} \right],{B_3}=\left[ {\begin{array}{@{}c@{}} { - b + 6}\\ { - 1} \end{array}} \right]\nonumber\end{gather}

functions of the three fuzzy rules are as follows:

\begin{align*} & {M_1}(t )=\frac{{\cos ({10{x_1}(t )} )+ 1}}{4},\quad {M_2}(t )=\frac{{\sin ({10{x_1}(t )} )+ 1}}{4},\nonumber\\ & {M_3}(t )=\frac{{ - \cos ({10{x_1}(t )} )- \sin ({10{x_1}(t )} )+ 1}}{4} \end{align*}

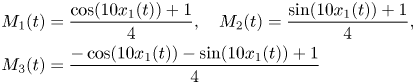
The computer simulation is performed in the initial state $x(0 )={\left[ {\begin{array}{*{20}{c}} { - 2}& 1 \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} 1& 2 \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} { - 1}& { - 2} \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} 2& { - 1} \end{array}} \right]^T}$ in a purely controlled and non- piecewise manner, and the respective energy function $Q(x )A_i^T(x )+ F_i^T(x )B_i^T(x ) + \mathrm{\ \star }\mathrm{\ < }0$ diagrams are obtained.

After computer simulation, we get results as follows, respective piecewise Lyapunov matrices ${Q_\textrm{l}}(x )$ for

\[{Q_1}(x )=\left[ {\begin{array}{*{20}{c}} {0.52x_1^2 + 0.15345x_2^2}& 0\\ 0& {0.15345x_1^2 + 0.045266x_2^2} \end{array}} \right]\]

\[{Q_2}(x )=\left[ {\begin{array}{*{20}{c}} {0.51553x_1^2 + 0.15227x_2^2}& 0\\ 0& {0.15227x_1^2 + 0.044954x_2^2} \end{array}} \right]\]

\[{Q_3}(x )=\left[ {\begin{array}{*{20}{c}} {0.51122x_1^2 + 0.1507x_2^2}& 0\\ 0& {0.1507x_1^2 + 0.044353x_2^2} \end{array}} \right]\]

The controller Kil is as follows:

\[{K_{11}}=\left[ {\begin{array}{*{20}{c}} { - 0.08675x_1^2 - 0.6741}& { - 0.03222x_2^2 + 2.6102} \end{array}} \right]\]

\[{K_{21}} = \left[ {\begin{array}{*{20}{c}} { - 0.02481x_1^2 + 0.0781}& {0.0802x_2^2 + 0.4386} \end{array}} \right]\]

\[{K_{31}}=\left[ {\begin{array}{*{20}{c}} { - 0.01089x_1^2 - 1.1141}& { - 0.02357x_2^2 - 0.9996} \end{array}} \right]\]

\[{K_{12}}=\left[ {\begin{array}{*{20}{c}} { - 0.08744x_1^2 - 0.6782}& {0.03236x_2^2 + 2.6279} \end{array}} \right]\]

\[{K_{22}}=\left[ {\begin{array}{*{20}{c}} { - 0.02502x_1^2 + 0.0765}& {0.0806x_2^2 + 0.4392} \end{array}} \right]\]

\[{K_{32}}=\left[ {\begin{array}{*{20}{c}} { - 0.01097x_1^2 - 1.0965}& {0.02403x_2^2 - 0.9669} \end{array}} \right]\]

\[{K_{13}}=\left[ {\begin{array}{*{20}{c}} { - 0.088x_1^2 - 0.6893}& {0.03277x_2^2 + 2.6379} \end{array}} \right]\]

\[{K_{23}}=\left[ {\begin{array}{*{20}{c}} { - 0.02514x_1^2 + 0.0741}& {0.08177x_2^2 + 0.4391} \end{array}} \right]\]

\[{K_{33}}=\left[ {\begin{array}{*{20}{c}} { - 0.01103x_1^2 - 1.1293}& { - 0.02346x_2^2 - 1.0156} \end{array}} \right]\]

Then we have the initial state $x(0 )={\left[ {\begin{array}{*{20}{c}} { - 2}& 1 \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} 1& 2 \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} { - 1}& { - 2} \end{array}} \right]^T},{\left[ {\begin{array}{*{20}{c}} 2& { - 1} \end{array}} \right]^T}$ similarly to get their respective energy function diagrams.

5. Discussion, conclusion and future study

In the previous literature on analysis of Lyapunov functions, when trying to deal with the differentiation of polynomial Lyapunov functions, the differential term of P(x) will be generated, which needs to be avoided through complicated methods, and this paper quotes Euler polynomial theorem homogeneous functions dealing with this problem, and constructs the Hessian matrix relationship between V(x) and$\dot{V}(x )$, successfully avoiding the problem of differential terms.

In terms of computer simulation, this method is demonstrated feasibly to converge the system that is difficult to be stabilised. It proves that it increases the degree of relaxation of the solution. A major advantage of increasing the degree of relaxation comes from $\sum\nolimits_{\textrm{s} = 1}^N {{\lambda _s}({{P_s}(x )- {P_\textrm{l}}(x )} )}$, but the selection and adjustment of ${\lambda _s}$ is an optimal process, which is different for each individual system. According to whether the energy function ${V_\textrm{l}}(x )$ is interleaving or converged, we can adjust the stabilisation straightforwardly and easily.

The future study directions will emphasise a multi-agent paradigm for UAV system design, on the basis of the proposed consensus-based GDM model, we will train in defining cooperation assignment activities aimed, instead, at the UAV consensus in the scene interpretation. An LMI (linear matrix inequality) program will occupy the hardware resources of the computer when it is executed, so if the matrix parameters to be solved are defined to be too high or too complicated, it will be difficult. It may cause the solution time to be too long, or there may even be insufficient memory capacity to execute. In terms of computer demonstrations, the sum-of-squares method is used to test the stability conditions of the fuzzy system, and a static feedback gain is designed to achieve stabilisation with a fuzzy controller based on the effective and efficient results of a nonlinear system as an example.