1. INTRODUCTION
Global Navigation Satellite System (GNSS) technologies such as the Global Positioning System (GPS) for maritime navigation must conform to the relevant standards of accuracy, integrity, continuity, and availability for a particular area, route, procedure, or operation (Lee et al., Reference Lee, Dyke, Decleene, Studenny and Beckmann1996; IMO Resolution MSC 90, 2012). The integrity is a measure of the degree of trust that can be placed in the correctness of the navigation information, which is typically addressed using the technique of Receiver Autonomous Integrity Monitoring (RAIM).
Since GNSS signals are vulnerable to disruption by environmental and man-made interference (accidental or deliberate), they would not meet all of the emerging performance requirements of robustness, integrity and availability for critical near-shore and in-harbour applications. Locata, a ground-based positioning system with configurable constellation design, can help to ensure availability and continuity of Position, Navigation and Timing (PNT) services, even when individual GNSS services are disrupted. Since 2002, Locata technology has been investigated for its feasibility as an alternative ground-based positioning technology. The fundamentals of the Locata technology and some results of consecutive tests, for different applications have been reported in the literature (e.g., Barnes et al., Reference Barnes, Rizos, Wang, Meng, Dodson and Roberts2003, Reference Barnes, Rizos and Kanli2004; Choudhury et al., Reference Choudhury, Rizos and Harvey2009; Li and Rizos Reference Li and Rizos2010; Montillet et al., Reference Montillet, Roberts, Hancock, Meng, Ogundipe and Barnes2009; Rizos et al., Reference Rizos, Roberts, Barnes and Gambale2010; Jiang et al., Reference Jiang, Li and Rizos2013). In these papers the feasibility of Locata technology for various environments have been investigated, including using Locata technology for indoor precise positioning, for bridge deformation monitoring, to achieve sub-centimetre level error of a Locata rover's position through static and kinematic tests, or to realise precise positioning in urban canyons. Such studies have demonstrated the feasibility of using this technology for a wide range of positioning applications. Unlike the GPS satellite constellation, the distribution of Locata transmitters can be designed beforehand with the necessary geometric characteristics so as to improve the system integrity. It is therefore of value to investigate the influence of LocataNet configuration design on RAIM performance.
One important step in RAIM is the Fault Detection and Exclusion (FDE) process. The purpose of FDE is to detect the presence of unacceptably large position errors, and then to exclude the source that causes the errors. To achieve this goal, a number of FDE algorithms for GPS navigation have been published over the past few decades. Lee (Reference Lee1986) first introduced a range-comparison method to detect GPS satellite failure. Parkinson and Axelrad (Reference Parkinson and Axelrad1987) suggested a least-squares residual method for autonomous GPS satellite failure detection and exclusion. Sturza (Reference Sturza1988) proposed the standard parity space algorithm to detect satellite failure, and then to exclude measurements from the failed satellite. However, the FDE algorithms used in these earlier studies are for static scenarios and depend only on the current measurements. Sequential RAIM algorithms implemented via the Kalman filter and other multiple-epoch measurement methods have also been proposed (Yang et al., Reference Yang, Chang and Fan2001; Tsai et al., Reference Tsai, Chang and Yang2004). Methods of detecting and excluding faults with multiple sensors have recently been investigated (Guerrier et al., Reference Guerrier, Waegli, Skaloud and Victoria-Feser2012).
In addition to providing real-time alerts of satellite failure, a GPS-RAIM system is also expected to provide a performance index relative to the level of position error being protected (Brown and Chin, Reference Brown and Chin1997). The idea of computing such an on-line performance index dates back to the early 1990s with papers by Brenner (Reference Brenner1990) and Brown and Sturza (Reference Brown and Sturza1990). Various names have been given to the RAIM performance indicators. The most commonly used are Horizontal Protection Level (HPL) and Vertical Protection Level (VPL). A variety of methods have been proposed for determining approximations to HPL and VPL (Milner and Ochieng Reference Milner and Ochieng2010; Wu et al., Reference Wu, Wang and Jiang2013). The influence of the correlation coefficient between any two test statistics on the FDE performance was studied by Knight et al., (Reference Knight, Wang and Rizos2010) and Yang et al. (Reference Yang, Wang, Knight and Shen2013a). However, no matter which indicator is used, the performance of GPS-RAIM is most strongly influenced by the satellite geometry.
This paper aims to study the influence of LocataNet configuration design on the performance of the Locata positioning system, with an emphasis on its potential use in port environments. The paper is organised as follows. The fundamental measurement model of the Locata technology is described in Section 2. The RAIM-based FDE method is introduced, and different indicators of RAIM performance are discussed in Section 3. In Section 4, data from a field trial conducted on Sydney Harbour are used to analyse the RAIM characteristics of the LocataNet configuration design. Section 5 then presents the concluding remarks.
2. MATHEMATICAL MODEL OF LOCATA TECHNOLOGY MEASUREMENTS
Locata is a ground-based positioning system that transmits ranging signals at frequencies in the 2·4 GHz industrial, scientific and medical (ISM) radio band. Such ranging signals, from transmitters known as ‘LocataLites’, can be tracked by a Locata receiver. A Locata network, or ‘LocataNet’, consists of at least four time-synchronised LocataLites within a single network (Barnes et al., Reference Barnes, Rizos, Wang, Meng, Dodson and Roberts2003; Rizos et al., Reference Rizos, Roberts, Barnes and Gambale2010). The ‘user segment’ includes any number of fixed or moving Locata user receivers, or ‘rovers’, operating within the service area to derive their own positions using the signals transmitted by the LocataLites. It has been reported that the operating range of a LocataNet can be up to 50 km, with adequate transmission signal power (Locata Corporation, 2011).
2.1. Locata measurement
Similar to GNSS, Locata range measurements include pseudorange and carrier phase. Pseudorange measurements are an estimate of the distance between a LocataLite and a Locata user receiver. The carrier phase measurements are more precise than pseudorange measurements, and the positioning results are more accurate after the ambiguities are reliably estimated. The basic Locata pseudorange and carrier phase observation equation between receiver and LocataLite channel i for a single frequency can be expressed as
$$\left\{ {\matrix{ {P^i = r^i + \delta T^i + c \cdot \delta t + \varepsilon _P^i} \cr {\lambda \cdot \varphi ^i = r^i + \delta T^i + c \cdot \delta t + \lambda \cdot N^i + \varepsilon _\varphi ^i} \cr}} \right.$$where Pi and φi are the pseudorange and carrier phase measurement; ri is the geometric distance from LocataLite i to the receiver, δTi is the tropospheric delay (estimated with a suitable correction model); c is the speed of light, δt. is the unknown receiver clock bias that can be considered in the estimation process or eliminated by single-differencing measurements; λ is the wavelength (depending on frequency); Ni is the carrier phase ambiguity; ε Pi and ε φi are unmodelled residual errors due to multipath, scattering and any other source on pseudorange and carrier phase, respectively. These residual errors are typically assumed to be normally distributed.
Unlike GNSS there is no transmitter clock error present in the Locata observation equation because of the tight time synchronisation of the LocataLites (Locata Corporation, 2011). Ambiguities in the carrier phase measurements are typically estimated as floating-point values, and can be resolved using either a known-point-initialisation or on-the-fly resolution techniques (Jiang et al., Reference Jiang, Li and Rizos2013).
The generalised linear observation equation for Locata positioning of Equation (1) can be simplified as
$${\bi l} = {\bi Ax} + {\bi \varepsilon} $$where l is the measurement residual vector, A is the design matrix related to the geometric distribution of LocataLite transmitters, x is the unknown vector that may include position, velocity, and ambiguities (if carrier phase measurements are used).
Optimal estimates for the parameter x can be obtained in terms of the least-squares (LS) procedure based only on the measurement model of Equation (2), or using a Kalman filter (KF) with appropriate dynamic and measurement models. Since the KF algorithm can be converted to the equivalent LS estimation (Hewitson and Wang, Reference Hewitson and Wang2010), the RAIM mathematical model in the work presented here is based on the LS procedure.
2.2. Locata/GPS integration schemes
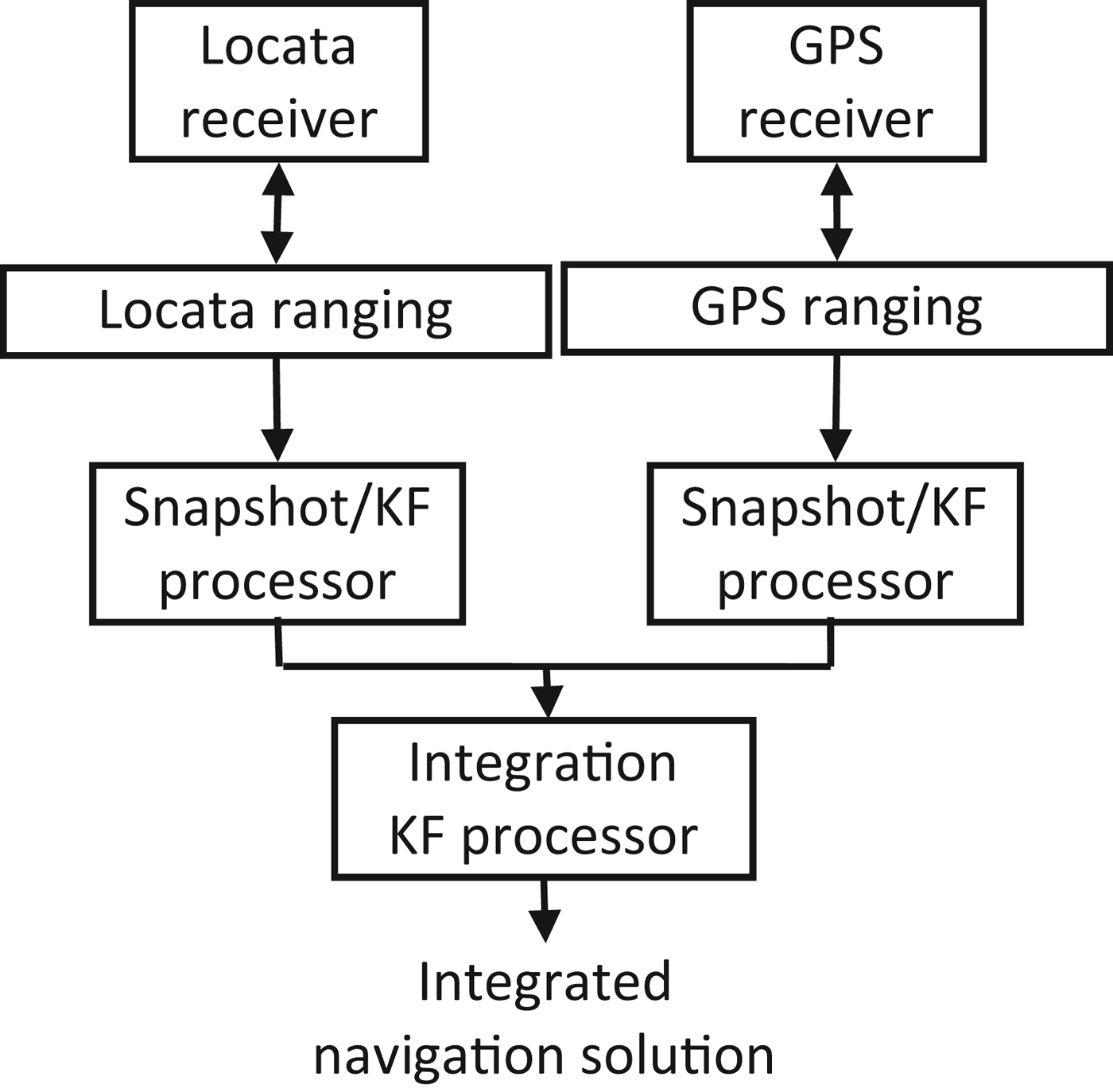
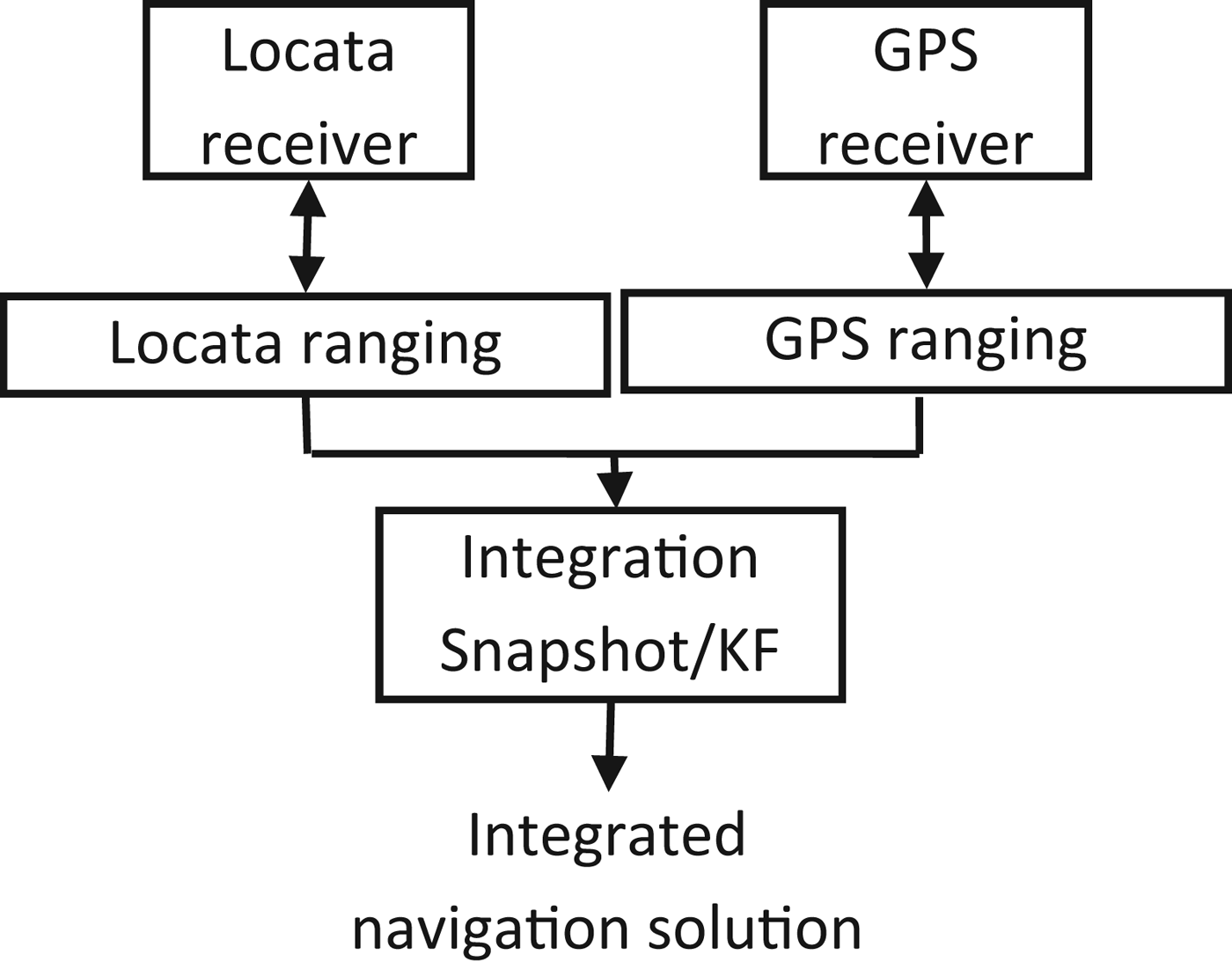
Locata can be used independently or as an augmentation to GPS, thus the integration strategies are worthy of discussion. The two types of Locata/GPS integration algorithms, loosely-coupled and tightly-coupled, are shown in Figures 1 and 2 respectively. In the loosely-coupled scheme the GPS and Locata measurements are processed separately, and these solutions are integrated using a KF. In such an integration scheme two parallel processors are required, however it can be easily extended to incorporate data from additional sensors.
Figure 1. Loosely-coupled GPS/Locata integration architecture.
Figure 2. Tightly-coupled GPS/Locata integration architecture.
Figure 2 shows the tightly-coupled integration scheme, in which GPS and Locata are integrated at the measurement level. In terms of solution accuracy, these two schemes are, in principle, equivalent. However, from the point of view of FDE by fusing measurements from two separate navigation sub-systems using the tightly-coupled approach, the measurement redundancy increases. Therefore the system integrity and navigation continuity, which rely on the degree of redundancy, will be improved. In this paper the tightly-coupled approach is used to investigate the performance of the Locata positioning system with or without GPS aiding, using the RAIM concept.
3. RAIM CONCEPT AND PERFORMANCE INDICATORS
3.1. Fault detection and exclusion
The most straightforward implementation of RAIM fault detection is based on the use of the magnitude of the parity (or) residual vector ||v|| as a statistical indicator of possible navigation failure (Brown and Chin, Reference Brown and Chin1997). Under normal error conditions v is zero-mean and Gaussian, and it follows that
$${\bi v}^{\rm T} {\bi v}/\sigma _0^2 \sim \chi ^2 (n - 4)$$Given a desired probability of false alarm a under normal error conditions, a threshold T d can be set analytically as
$$T_d = \chi _a^2 (n - 4)$$where χ a2(n−4) is the lower percentage point of the χ 2 distribution. Whenever the magnitude of the parity vector exceeds the threshold, a navigation failure is declared. That is
If: v Tv/σ 02⩾T d, declare “failure”
If: v Tv/σ 02<T d, declare “no failure”
Once a fault has been detected using the above global detection algorithm, the w-test can then be used to identify the corresponding measurement, where the test statistic is (Baarda, Reference Baarda1968)
$$w_i = \displaystyle{{{\bi c}_i^{\rm T} {\bi PQ}_{vv} {\bi Pl}} \over {\sqrt {{\bi c}_i^{\rm T} {\bi PQ}_{vv} {\bi Pc}_i}}} $$where Q vv=Q−A(A TPA)−1A T is the cofactor matrix of the estimated residuals (from the standard Gauss-Markov model), P is the weight matrix of measurement l, and ci=[0, ⋯, 0, 1, 0, ⋯, 0]T is a unit vector with the ith element equal to one. The outlier test statistic w i follows a standard normal distribution under the null hypothesis. When there is a fault with the size of ∇ i in ith observation, the expectation of the outlier statistic is (Baarda, Reference Baarda1968)
$$\delta _i = \displaystyle{{\nabla _i} \over {\sqrt {q_{\hat \nabla _i}}}} $$where 
$q_{\hat \nabla _i} = ({\bi c}_i^{\rm T} {\bi PQ}_{vv} {\bi Pc}_i )^{ - 1} $ is the cofactor matrix of the estimated fault.
3.2. Indicators of RAIM performance
The RAIM-based FDE algorithms are sensitive to geometric factors. From Equation (2), the corresponding LS position error under normal error conditions is then given by
$$\delta {\bi x} = {\bi \hat x} - {\bi x} = ({\bi A}^{\rm T} {\bi PA})^{ - 1} {\bi A}^{\rm T} {\bi \varepsilon} \sim N(0,{\bi \;} ({\bi A}^{\rm T} {\bi PA})^{ - 1} )$$In the LS algorithm Dilution of Precision (DOP) values are indicators for the estimated position accuracy. The smaller the DOP value, the higher the position accuracy. Different DOP values include
$$\left\{ {\matrix{ {PDOP = \sqrt {({\bi Q}_{xx} )_{11} + ({\bi Q}_{xx} )_{22} + ({\bi Q}_{xx} )_{33}}} \cr {HDOP = \sqrt {\left( {{\bi Q}_{xx}} \right)_{11} + \left( {{\bi Q}_{xx}} \right)_{22}} \;} \cr {VDOP = \sqrt {\left( {{\bi Q}_{xx}} \right)_{33}}} \cr}} \right.$$where Q xx=(A TPA)−1 is the cofactor matrix of unknown states. PDOP, HDOP and VDOP are the Position DOP, Horizontal DOP and Vertical DOP, respectively.
Besides the DOP values, the internal reliability is expressed as a Minimal Detectable Bias (MDB) that specifies the lower bound for detectable faults with a certain probability and confidence level. For the ith observation MDB can then be expressed as (Baarda, Reference Baarda1968; Teunissen, Reference Teunissen2006)
$$MDB\left( {\hat \nabla _i} \right) = \displaystyle{{\delta _0} \over {\sqrt {{\bi c}_i^T {\bi PQ}_v {\bi Pc}_i}}} $$where δ 0 is the theoretical non-centrality parameter that is computed from 
$\delta _0 = u_{1 - \alpha _0 /2} - u_{\beta _0} $ with α 0 denoting the level of significance of the test, and 1- β 0 denoting the power of the test. With the MDB related to the internal reliability, the external reliability indicates the influence of model errors of the size of the MDB on the position errors. From Equation (7), in the case of a bias ∇ i in the ith measurement, it can be written as
$$\delta {\bi x} = ({\bi A}^{\rm T} {\bi PA})^{ - 1} {\bi A}^{\rm T} {\bi Pc}_i \displaystyle{{\delta _0} \over {\sqrt {{\bi c}_i^T {\bi PQ}_v {\bi Pc}_i}}} $$Assuming the slope associated with ith satellite is given by
$$SLOPE_i = \sqrt {({\bi H}_{1i}^2 + {\bi H}_{2i}^2 )/({\bi R})_{ii}} $$where H=(A TPA)−1A TP and R=PQ vP, subscript i and j indicate the corresponding element in the matrix. Combining Equations (10) and (11)
$$\delta {\bi x}_{\rm H} = SLOPE_i \cdot \delta _0 $$where 
$\delta {\bi x}_{\rm H} = \sqrt {(\delta {\bi x}_{\rm E} )^2 + (\delta {\bi x}_{\rm N} )^2} $ is the horizontal position bias. Equation (12) is the estimated horizontal position bias generated by the fault in the ith measurement with a preset non-centrality parameter δ 0. Since the actual position of the fault is unknown, with the maximum slope among all the measurements
$$SLOPE_{\rm MAX} = \max (SLOPE_i )$$the horizontal position bias will always be smaller than the protection radius obtained from
$$Protection\; Radius = SLOPE_{{\rm MAX}} \cdot \delta _0 $$if no fault is declared. Consequently, under certain circumstances the protection radius parameter can be a good approximation to the true horizontal error that can be protected in the presence of noise.
The above analysis indicates the position accuracy assuming no fault and the position bias when a fault cannot be detected with the desired false alarm probability and missed detection probability. In addition, the ability of isolating and excluding the fault, known as ‘separability’, should also be evaluated. The separability of two failure modes can be evaluated by the correlation coefficient between them, expressed as
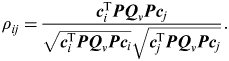$$\rho _{ij} = \displaystyle{{{\bi c}_i^{\rm T} {\bi PQ}_v {\bi Pc}_j} \over {\sqrt {{\bi c}_i^{\rm T} {\bi PQ}_v {\bi Pc}_i} \sqrt {{\bi c}_j^{\rm T} {\bi PQ}_v {\bi Pc}_j}}}. $$It is clear that if |ρ ij| is close to 1 the separability between failure mode i and j is very weak, hence it is difficult to separate the two failure modes. On the other hand, if |ρ ij| is close to zero, the failure mode i and j are much easier to separate.
4. EXPERIMENT AND ANALYSES
4.1. The experiment
To assess the performance of Locata positioning technology with a specific LocataNet configuration design, data from a survey vessel was used for the analysis reported in this paper. The experiment was conducted in October 2012 in Sydney Harbour, on the fringes of Sydney's central business district, where it was found that the GPS signals were frequently blocked. The LocataNet comprised eight LocataLites, six of which were installed along the shore, and the remaining two were located further away, with one on the Harbour Bridge itself (LL7) and the other at Kirribilli (LL8). They were time-synchronised with the master LocataLite configured for synchronisation with respect to GPS time. According to the standard of IMO Resolution A. 1046 (2011), the output rates of GPS and Locata were set to 1s, and the Locata signal availability was 99·87% within the shore area. The rover trajectory and the location of the LocataLites are shown in Figure 3. The coordinates of each LocataLite are listed in Table 1, which show the LocataNet covered a volume of approximately 1000*2000*100 metres (in east-north-up directions). The main sailing area was near the shore close to LocataLites LL1 to LL5.
Figure 3. LocataNet configuration and approximate rover trajectory.
Table 1. Coordinates of the LocataLites (unit: metres).
4.2. DOP analysis
To investigate the positioning performance the HDOP and VDOP values are respectively shown in Figure 4, with LocataLites marked as red points and tagged with labels.
Figure 4. HDOP and VDOP values of LocataNet.
Figure 4(a) shows the best HDOP values, smaller than 2, are concentrated near the shore area. When the vessel moves outside this area the HDOP values increase gradually and reach values up to around 10. Hence using this LocataNet configuration design the horizontal positioning accuracy near the shore area should be high. Figure 4(b) shows the distribution of VDOP values, which are the best for the area between LL6 and LL7, even better than at the main shore area served by LL1 to LL5. This is because the height of LL7 is quite different compared to the other LocataLites, as shown in Table 1. The height difference between LL6 and LL7 reaches 75 metres, while the heights of LL1 to LL5 are nearly the same, with a difference of less than 0·5 metres. Comparison of Figures 4(a) and 4(b) indicates that the VDOP values are nearly ten times worse than the HDOP values.
Since the LocataLites are typically set up on the ground, the vertical accuracy cannot be well controlled unless there is significant terrain variation. One method to improve the vertical positioning accuracy is to add altitude-related constraints, such as using tide height data for maritime applications (Jiang et al., Reference Jiang, Li and Rizos2013), or a non-holonomic constraint for vehicle navigation (Yang et al., Reference Yang, Li, Wu and Rizos2013b). In addition, some GPS measurements, although not sufficient to independently determine a position solution, can be used to enhance the geometric strength of the LocataNet, especially for the vertical component. To investigate the influence of GPS-aided Locata, the HDOP and VDOP values assuming the addition of two and three GPS satellites are shown in Figure 5, by setting the cut-off elevation angle as 50° and 45° respectively.
Figure 5. HDOP and VDOP values with GPS aiding.
Figure 5 shows that both the HDOP and VDOP values are improved by the addition of several GPS measurements. When two GPS satellites are used, the HDOP and VDOP values decrease to less than 3 and 8 respectively. Compared with Figure 4, this is a two times improvement in HDOP and nearly eight times improvement in VDOP. When the third GPS satellite (with an elevation angle of 49°) is added, the geometry strength is further enhanced. This demonstrates the advantage of tightly-coupling the simultaneous processing of GPS and Locata measurements, even when GPS measurements on their own are insufficient for standalone positioning.
4.3. Internal reliability analysis
In order to investigate internal reliability, the MDB value associated with each LocataLite was calculated, and the values for LL1, LL2, LL7 and LL8 are shown in Figure 6. Note an interesting phenomenon: the MDB generally increases when the vessel is sailing close to that particular LocataLite. As expected, the MDB values vary in the different directions. The closer the vessel is to the LocataLite, the larger the variation is. This means the internal reliability cannot be kept stable when near a LocataLite. To avoid this unfavourable situation, the rover must keep a certain distance away from the LocataLites. In some directions the stability of the internal reliability is independent of the distance between the LocataLite and the rover. Thus the azimuth has more influence on the internal reliability as well as the distance.
Figure 6. MDB values for each LocataLite.
The LL1 and LL2 are close to where the vessel is sailing, thus the variation of their MDBs is similar, with the smallest values occurring near LL6 and LL7. The MDB distributions for LL3 to LL5 are similar to the case of LL1 and LL2, and thus not presented here. Figures 6(c) and 6(d) show the MDBs of LL7 and LL8 respectively, changing from 10 to 60 and from 50 to 450 within the whole test area, which is rather worse than those of LL1 to LL5. This indicates that the fault contaminating LL7 measurements would be quite difficult to identify. Furthermore, identifying a fault in LL8 measurements is almost impossible. With the results presented here, one can pre-compute the possibility of successfully identifying a fault at each LocataLite, and assess the data quality and potential risk from each LocataLite.
4.4. Analysis of external reliability
Figure 7 shows the change tendency of SLOPE MAX values across the test area. It indicates that the minimum SLOPE MAX values (less than 50) are spread across the area near LL5, LL6 and LL7. In contrast, the maximum values of SLOPE MAX mainly are near LL8, and are as large as 350. At the shore area near LL1 to LL5 the values of SLOPE MAX are between 50 and 100. This indicates that even in the main sailing area the horizontal protection level is 50 to 100 times the size of the noise, which means there is comparatively poor performance in terms of external reliability.
Figure 7. Maximum slope values.
To further study the influence of different LocataLites on protection levels the percentages of the location of the SLOPE MAX at the different LocataLites are plotted in Figure 8. One can see that more than 90% of the SLOPE MAX values are at LL7 and LL8, indicating that LL7 or LL8 are the crucial elements that will degrade the positioning accuracy severely, even in the presence of a small measurement fault. Considering the corresponding MDBs in Figure 6, it further reveals that measurements from LL7 and LL8 are of poor internal and external reliability. In other words, faults in measurements at these two LocataLites are difficult to detect and the undetected faults will severely bias a positioning solution.
Figure 8. Percentages of locations of the SLOPE MAX.
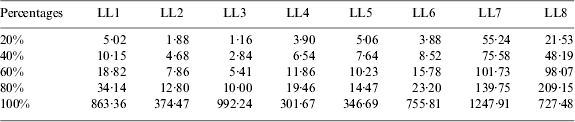
To show the differences of external reliabilities on LocataLites, the SLOPE values of each LocataLite are listed in Table 2. It can be seen that 60% of the SLOPE values for LL1 to LL6 are less than 20, while more than 80% of the values for LL7 and LL8 are greater than 20. All of these SLOPE values increase dramatically between the percentages of 80% to 100%. These significant increases occur in areas beyond the coverage of the LocataNet. Thus in order to satisfy reliability requirements, the optimal sailing area is actually much smaller than the signal coverage area serviced by these LocataLites.
Table 2. SLOPE values of each LocataLite at different percentages.
4.5. Analysis of correlation coefficient
To investigate the separability between any two LocataLites within the test area, the correlation coefficients of LocataLite pairs LL1-LL2, LL1-LL3, LL6-LL7, and LL6-LL8 are shown in Figure 9. Separability refers to the capability of correctly distinguishing one faulty measurement from another one. The smaller the correlation coefficient, the better the separability.
Figure 9. Correlation coefficient between two LocataLites.
Figure 9(a) indicates that near the area to the right of LL1 and LL2 the correlation coefficient is less than 0·2, indicating a good separability. At the shore area most correlation coefficients between LL1 and LL2 are less than 0·6. The worst area for distinguishing the fault between LL1 and LL2 measurements is near LL6, LL7 and LL8. Figure 9(b) indicates a better separability between LL1 and LL3 where most correlation coefficients are less than 0·5, even in the area far away from the shore. Figure 9(c) illustrates a rather poor situation between LL6 and LL7. In most of the test area the correlation coefficients are as high as 0·9, which means a fault cannot be distinguished between the two LocataLites. Figure 9(d) shows that the correlation coefficients between LL6 and LL8 are below 0·6 at the shore, and are rather large outside the area. This means the capability of identifying a fault between LL6 and LL8 will degrade severely. Overall, fault identification between LL1 and LL3 is the easiest, while distinguishing between LL6 and LL7 is nearly impossible.
To evaluate the overall separability of each LocataLite, the cumulative distribution probabilities of the correlation coefficient between one LocataLite and all the others are presented in Figure 10. For LL1 to LL5, 80% of their correlation coefficients with other LocataLites are less than 0·6. On the other hand, correlation coefficients larger than 0·8 take higher percentages for LL6, LL7 and LL8. This indicates better separability of LocataLites LL1 to LL5, compared with LL6, LL7 and LL8.
Figure 10. Cumulative distribution function of correlation coefficient for each LocataLite.
5. CONCLUDING REMARKS
This paper investigated the influence of LocataNet configuration design on RAIM performance. The analysis results have demonstrated that with a specific LocataNet configuration in a Sydney Harbour Test, horizontal position accuracies are highest near the shore area, while vertical position accuracies are not as good as horizontal position accuracies due to the limited geometric strength in the vertical component. With the augmentation of two to three GPS satellites, the HDOP and VDOP values are both improved dramatically, nearly twice and eight times for horizontal and vertical directions respectively. Compared with LL1 to LL6, the internal and external reliability of LL7 and LL8 are much weaker. This means the robustness of measurements from these two LocataLites are quite poor due to their geometric locations. It therefore can be determined beforehand that any faults which contaminate these two LocataLites are difficult to detect, and will bias the position solutions. The distribution of correlation coefficients between any two LocataLites also reveals that the separability characteristics among LL6, LL7 and LL8 are rather weak, indicating a large possibility of wrong exclusion if faults occur in any of the measurements from these LocataLites.
In general RAIM analyses provide a confidence measure that can be computed in advance. The experimental results presented in this paper show that this specific LocataNet configuration design provides the best performance near the shore area (covered by LL1 to LL5), in terms of position accuracy, internal and external reliability, as well as separability. When the vessel is sailing beyond this near-shore area the navigation performance of the Locata system will degrade quickly.
