Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T12:22:47.876Z Has data issue: false hasContentIssue false
  • English
  • Français

A Steady Creep Theory of High Lead Pb/Sn Solder with Creep-Parameters Maps

Published online by Cambridge University Press:  05 May 2011

C. F. Lee ,
J. J. Wang  and
W. K. Chung
C. F. Lee*
Affiliation:
Department of Engineering Science, National Cheng-Kung University, Tainan, Taiwan 70101, R.O.C.
J. J. Wang*
Affiliation:
Department of Engineering Science, National Cheng-Kung University, Tainan, Taiwan 70101, R.O.C.
W. K. Chung*
Affiliation:
Nanya Technology Corporation, Assy/Tect Eng. Section, Taoyuan, Taiwan 333, R. O. C.
*
*Professor
** Graduate student
*** Engineer
Get access

Abstract

In this paper, Valanis' steady creep theory with four creep parameters 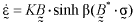was derived from a liaison of the theory of deformation kinetics with internal isotropy and the theory of irreversible thermodynamics of continuous media with only one internal state variable.

According to the theory, steady creep rates under simple shear and simple tensile conditions are related and allow one to construct creep-parameters maps of high lead Pb/Sn solders (from 90% to 100% Pb). When testing temperatures are higher than solder's solvus temperature, microstructural transformation from lamellae α + β phase to solid solution α phase in the bulk specimens are considered in the construction of maps. Applications of maps in the 97.5Pb/2.5Sn solder joints creep tests need minor modifications due to dispersive precipitation of tin particles in lead matrix. As a result, the maps may provide estimated steady creep rates for the usage of finite elements analysis in the microsystem or electronic packaging analysis.

Keywords

Steady creep theorySn/Pb creep-parameters mapsBulk and joint specimens
Type
Articles
Information
Journal of Mechanics , Volume 21 , Issue 4 , December 2005 , pp. 217 - 225
Copyright
Copyright © The Society of Theoretical and Applied Mechanics, R.O.C. 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Darveaux, R. and Benerji, K., “Constitutive Relations for Tin-Based Solder Joints,” IEEE Trans. Components, Hybrids and Manufacturing Technology, 15(6), pp. 1013–1024 (1992).CrossRefGoogle Scholar
2.McDowell, D. L., Miller, M. P. and Books, D. C., “A Unified Creep-Plasticity Theory for Solder Alloys,“Fatigue of Electronic Materials, Schroeder, S. A. and Mitchell, M. R., Eds., ASTM STP 1153, pp. 42–59 (1994).CrossRefGoogle Scholar
3.Maciucescu, L., Sham, T. L. and Krempl, E., “VBO: A State Variable Constitutive Equation for a Solder Alloy,” ASME EEP., 19–2, Advance in Electronic Packaging, pp. 1615–1621 (1997).Google Scholar
4.Sasaki, K., Ohguchi, K-I, and Ishikawa, H., “Viscoplastic Deformation of 40Pb/60Sn Solder Alloys-Experiments and Constitutive Modeling,” J. Electronic Packaging, ASME, pp. 379–387 (2001).CrossRefGoogle Scholar
5.Valanis, K. C., “Deformation Kinetics in Three Dimensions,” Int. J. Engng. Sci., 22(8–10), pp. 979–988 (1984).CrossRefGoogle Scholar
6.Krausz, A. S. and Eyring, H., Deformation Kinetics, Wiley, New York (1975).Google Scholar
7.Valanis, K. C. and Lalwani, S. A., “Thermodynamics of Internal Variables in the Context of Absolute Reaction Rate Theory,” J. Chm. Phys., 67, pp. 3980–3990 (1997).CrossRefGoogle Scholar
8.Valanis, K. C. and Lee, C. F., “Deformation Kinetics of Steady-State Creep in Metals,” Int. J. Solids Structures, 17, pp. 589–604 (1981).CrossRefGoogle Scholar
9.Lee, C. F., Chang, M. K. and Chung, W. K., “Deformation Kinetics of Steady Creep in Sn/Pb Solder Alloys with Applications,” J. of Mechanics, 20(2), pp. 35–41 (2004).CrossRefGoogle Scholar
10.Mohamed, F. A., Murry, K. L. and Morris, J. W. Jr, “Haper-Dorn Creep in Al, Pb, and Sn,” Met. Trans., 4, pp. 935–940 (1973).CrossRefGoogle Scholar
11.Forst, H. J., Howard, R. T., Lavery, P. R. and Lutender, S. D., “Creep and Tensile Behavior of Lead-Rich Lead-Tin Solder Alloys,” IEEE Trans. Components, Hybrids, and Manufacturing Technology, 11(4), pp. 371–379 (1988).CrossRefGoogle Scholar
12.Ashby, M. F. and Jones, D. R. H., Engineering Materials, 2, Fig. 3.1, Pergamon Press, Oxford, p. 24 (1986).Google Scholar