No CrossRef data available.
Article contents
Simulation of pulse-induced nonthermal dynamics of molecules encapsulated in carbon nanotubes
Published online by Cambridge University Press: 02 January 2013
Abstract
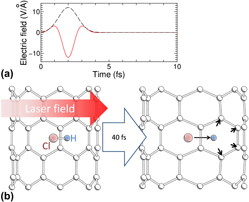
Density functional theory, which can be used for simulating the properties of materials in the electronic ground state, was extended to time-dependent density functional theory (TDDFT). This extension enabled us to simulate nonthermal (nonequilibrium) dynamics under electronic excitation as well as to analyze and predict phenomena observed in experiments using femtosecond lasers. In this invited paper, a numerical simulation based on TDDFT for laser-induced dynamics of molecules encapsulated in carbon nanotubes (CNTs) is presented. Fast motion of molecules can be induced by short strong laser pulses that cause electronic excitation. The role of CNTs is not simply trapping the molecules but also modulating the electric field of the laser pulse. This knowledge of microscopic-scale processes will be useful when using CNTs as nanoscale test tubes in future photochemistry experiments in confined spaces for the synthesis of exotic materials. The numerical scheme and detailed results of the simulation are also presented here.
- Type
- Invited Feature Paper
- Information
- Copyright
- Copyright © Materials Research Society 2013


