Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T11:28:49.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple nanoindentation-based method for determining linear thermal expansion coefficients of micro-scale materials

Published online by Cambridge University Press:  24 November 2020

Yuanbin Qin Open the ORCID record for Yuanbin Qin [Opens in a new window] ,
Zhiyu Nie ,
Chao Ma ,
Longchao Huang ,
Yueqing Yang ,
Qinqin Fu ,
Weifeng He  and
Degang Xie
Yuanbin Qin
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
Zhiyu Nie
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
Chao Ma
Affiliation:
Center for High Resolution Electron Microscopy, College of Materials Science and Engineering, Hunan University, Changsha410082, P.R. China
Longchao Huang
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
Yueqing Yang
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
Qinqin Fu
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
Weifeng He
Affiliation:
Science and Technology on Plasma Dynamics Laboratory, Air Force Engineering University, Xi'an 710038, P.R. China
Degang Xie*
Affiliation:
Center for Advancing Materials Performance from the Nanoscale, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P.R. China
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

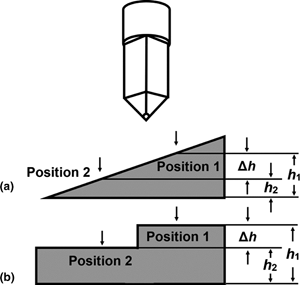
The thermal expansion coefficient (CTE) is a vital design parameter for reducing the thermal-stress-induced structural failure of electronic chips/devices. At the micro- and nano-scale, the typical size range of the components in chips/devices, the CTEs are probably different from that of the bulk materials, but an easy and accurate measurement method is still lacking. In this paper, we present a simple but effective method for determining linear CTEs of micro-scale materials only using the prevalent nanoindentation system equipped with a heating stage for precise temperature control. By holding a constant force on the sample surface, while heating the sample at a constant rate, we measure two height–temperature curves at two positions, respectively, which are close to each other but at different heights. The linear CTE is obtained by analyzing the difference of height change during heating. This method can be applied to study the size effect or surface effect of CTE of embedded micro-scale structures, aiding the failure analysis and structural design in the semiconductor industry.

Keywords

micro-scalenanoindentationAlTifilm
Type
Article
Information
Journal of Materials Research , Volume 35 , Issue 23-24 , 14 December 2020 , pp. 3202 - 3209
Check for updates
Copyright
Copyright © The Author(s), 2020, published on behalf of Materials Research Society by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chi, H.P.: A simple method for determining linear thermal expansion coefficients of thin films. J. Micromech. Microeng. 12, 548 (2002).Google Scholar
Lerch, P., Slimane, C.K., Romanowicz, B., and Renaud, P.: Modelization and characterization of asymmetrical thermal micro-actuators. J. Micromech. Microeng. 6, 134 (1996).CrossRefGoogle Scholar
Pan, C.S. and Hsu, W.: An electro-thermally and laterally driven polysilicon microactuator. J. Micromech. Microeng. 7, 7 (1997).CrossRefGoogle Scholar
Mayrhofer, P.H., Kunc, F., Musil, J., and Mitterer, C.: A comparative study on reactive and non-reactive unbalanced magnetron sputter deposition of TiN coatings. Thin Solid Films 415, 151 (2002).CrossRefGoogle Scholar
Bielawski, M.: Residual stress control in TiN/Si coatings deposited by unbalanced magnetron sputtering. Surf. Coat. Technol. 200, 3987 (2006).CrossRefGoogle Scholar
Pierson, H.O.: Handbook of Refractory Carbides and Nitrides: Properties, Characteristics, Processing and Applications (Noyes Publications, NJ, USA, 1996), p. 186.Google Scholar
Fang, W. and Wickert, J.A.: Comments on measuring thin-film stresses using bi-layer micromachined beams. J. Micromech. Microeng. 5, 276 (1995).CrossRefGoogle Scholar
Fang, W. and Lo, C.-Y.: On the thermal expansion coefficients of thin films. Sens. Actuators A 84, 310 (1999).CrossRefGoogle Scholar
Von Arx, M., Paul, O., and Baltes, H.: Process-dependent thin-film thermal conductivities for thermal CMOS MEMS. J. Microelectromechan. Syst. 9, 136 (2000).CrossRefGoogle Scholar
Fang, W. and Wickert, J.A.: Determining mean and gradient residual stresses in thin films using micromachined cantilevers. J. Micromech. Microeng. 6, 301 (1996).CrossRefGoogle Scholar
Vlassak, J.J. and Nix, W.D.: A new bulge test technique for the determination of Young's modulus and Poisson's ratio of thin films. J. Mater. Res. 7, 3242 (1992).CrossRefGoogle Scholar
Jansen, E. and Obermeier, E.: Thermal conductivity measurements on thin films based on micromechanical devices. Diam. Relat. Mater. 5, 644 (1996).CrossRefGoogle Scholar
Jones, R.V. and Richards, J.C.S.: Recording optical lever. J. Sci. Instrum. 36, 90 (1959).CrossRefGoogle Scholar
Kinzly, R.E.: A new interferometer capable of measuring small optical path differences. Appl. Opt. 6, 137 (1967).CrossRefGoogle ScholarPubMed
Jacobs, S.F., Bradford, J.N., and Berthold, J.W.: Ultraprecise measurement of thermal coefficients of expansion. Appl. Opt. 9, 2477 (1970).CrossRefGoogle ScholarPubMed
Okada, Y. and Tokumaru, Y.: Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 56, 314 (1984).CrossRefGoogle Scholar
Fug, G., Gasparoux, H., and Piaud, J.J.: Thermal variation apparatus for X-ray diffraction experiments up to 3000 K. J. Phys. E Sci. Instrum. 5, 1222 (1972).CrossRefGoogle Scholar
Miksic, S., Sherman, G., and Lal, H.: High-temperature X-ray diffraction furnace using a thermal-image technique. J. Appl. Crystallogr. 9, 466 (1976).Google Scholar
Lyon, K.G., Salinger, G.L., Swenson, C.A., and White, G.K.: Linear thermal expansion measurements on silicon from 6 to 340 K. J. Appl. Phys. 48, 865 (1977).CrossRefGoogle Scholar
Okada, Y.: A high-temperature attachment for precise measurement of lattice parameters by Bond's method between room temperature and 1500 K. J. Phys. E Sci. Instrum. 15, 1060 (1982).CrossRefGoogle Scholar
Gadre, K.S. and Alford, T.L.: Crack formation in TiN films deposited on Pa-n due to large thermal mismatch. Thin Solid Films 394, 124 (2001).CrossRefGoogle Scholar
Zoo, Y., Adams, D., Mayer, J.W., and Alford, T.L.: Investigation of coefficient of thermal expansion of silver thin film on different substrates using X-ray diffraction. Thin Solid Films 513, 170 (2006).CrossRefGoogle Scholar
Champi, A., Lacerda, R.G., Viana, G.A., and Marques, F.C.: Thermal expansion dependence on the sp2 concentration of amorphous carbon and carbon nitride. J. Non Cryst. Solids 338–340, 499 (2004).CrossRefGoogle Scholar
Besozzi, E., Dellasega, D., Pezzoli, A., Mantegazza, A., Passoni, M., and Beghi, M.G.: Coefficient of thermal expansion of nanostructured tungsten based coatings assessed by substrate curvature method. Mater. Des. 137, 192 (2018).CrossRefGoogle Scholar
Olmos, D., Martínez, F., González-Gaitano, G., and González-Benitoa, J.: Effect of the presence of silica nanoparticles in the coefficient of thermal expansion of LDPE. Eur. Polym. J. 47, 1495 (2011).CrossRefGoogle Scholar
Zhang, X.R., Fisher, T.S., Raman, A., and Sands, T.D.: Linear coefficient of thermal expansion of porous anodic alumina thin films from atomic force microscopy. Nanosc. Microsc. Thermophys. Eng. 13, 243 (2009).CrossRefGoogle Scholar
González-Benito, J., Castillo, E., and Cruz-Caldito, J.F.: Determination of the linear coefficient of thermal expansion in polymer films at the nanoscale: Influence of the composition of EVA copolymers and the molecular weight of PMMA. Phys. Chem. Chem. Phys. 17, 18495 (2015).CrossRefGoogle ScholarPubMed
Zhao, J.H., Du, Y., Morgen, M., and Ho, P.S.: Simultaneous measurement of Young's modulus, Poisson ratio, and coefficient of thermal expansion of thin films on substrates. J. Appl. Phys. 87, 1575 (2000).CrossRefGoogle Scholar
Russell, A.M. and Cook, B.A.: Coefficient of thermal expansion anisotropy and texture effects in ultra-thin titanium sheet. Scr. Mater. 37, 1461 (1997).CrossRefGoogle Scholar
Lima, M.M.D., Lacerda, R.G., Vilcarromero, J., and Marques, F.C.: Coefficient of thermal expansion and elastic modulus of thin films. J. Appl. Phys. 86, 4936 (1999).CrossRefGoogle Scholar
Riethmuller, W. and Benecke, W.: Thermally excited silicon microactuators. IEEE Trans. Electron Devices 35, 758 (1988).CrossRefGoogle Scholar
Feng, R. and Farris, R.J.: The characterization of thermal and elastic constants for an epoxy photoresist SU8 coating. J. Mater. Sci. 37, 4793 (2002).CrossRefGoogle Scholar
Liou, H.C., Ho, P.S., and Stierman, R.: Thickness dependence of the anisotropy in thermal expansion of PMDA-ODA and BPDA-PDA thin films. Thin Solid Films 339, 68 (1999).CrossRefGoogle Scholar
Choy, C.L.: Chapter 4 Thermal expansivity of oriented polymers. In Developments in Oriented Polymers-1, Ward, I.M., ed. (Applied Science Publishers, London and NJ, England and USA, 1982), pp. 121.Google Scholar
Liu, S., Chevali, V.S., Xu, Z., Hui, D., and Wang, H.: A review of extending performance of epoxy resins using carbon nanomaterials. Compos. Part B 136, 197 (2018).CrossRefGoogle Scholar
Rimdusit, S. and Ishida, H.: Development of new class of electronic packaging materials based on ternary systems of benzoxazine, epoxy, and phenolic resins. Polymer 41, 7941 (2000).CrossRefGoogle Scholar