Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T17:54:18.475Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple model of plate-like crystallization with constant plate thickness

Published online by Cambridge University Press:  19 April 2013

Beata Misztal-Faraj
Beata Misztal-Faraj*
Affiliation:
Polymer Physics Department, Institute of Fundamental Technological Research, Polish Academy of Sciences, 02-106 Warsaw, Poland
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

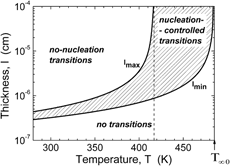
A kinetic model of crystallization based on two-dimensional nucleation and growth of plate-like crystals with constant thickness is analyzed. It is shown that plate thickness required for nucleation is limited. The lower limit is determined by zero Gibbs’ free energy of transition, the upper one corresponds to the conditions when the critical cluster volume of nucleation is equal to two elementary kinetic units. Effects of plate thickness on crystallization kinetics are discussed. In the lower temperature range, creation of thicker plates is preferred. For a given plate thickness, frequency of the phase transition decreases with increasing temperature. Numerical calculations for α-polypropylene concern kinetics of primary nucleation and global phase transition in a system of one or several fractions of plate-like kinetic elements.

Type
Articles
Information
Journal of Materials Research , Volume 28 , Issue 9 , 14 May 2013 , pp. 1224 - 1238
Copyright
Copyright © Materials Research Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ziabicki, A. and Misztal-Faraj, B.: Modeling of phase transitions in three-phase polymorphic systems: Part I. Basic equations and example simulation. J. Mater. Res. 26(13), 1586–1595 (2011).CrossRefGoogle Scholar
Misztal-Faraj, B. and Ziabicki, A.: Modeling of phase transitions in three-phase polymorphic systems: Part II. Effects of material characteristics on transition rates. J. Mater. Res. 26(13), 1596 (2011).CrossRefGoogle Scholar
Kolmogorov, A.N.: On statistical theory of metal crystallization. Izv. Akad. Nauk SSSR, Ser. Math. 3, 355 (1937).Google Scholar
Avrami, M.: Kinetics of phase change. I General theory. J. Chem. Phys. 7, 1103 (1939).CrossRefGoogle Scholar
Avrami, M.: Kinetics of phase change. II Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 8, 212 (1940).CrossRefGoogle Scholar
Avrami, M.: Granulation, phase change, and microstructure. Kinetics of phase change. III. J. Chem. Phys. 9, 177 (1941).CrossRefGoogle Scholar
Evans, U.R.: The laws of expanding circles and spheres in relation to the lateral growth of surface films and the grain-size of metals. Trans. Faraday Soc. 41, 365 (1945).CrossRefGoogle Scholar
Sajkiewicz, P., Gradys, A., Ziabicki, A., and Misztal-Faraj, B.: On the metastability of β phase in isotactic polypropylene: Experiments and numerical simulation. e-Polymers 124, 1–20 (2010).Google Scholar
Keller, A.: A note on single crystals in polymers: Evidence of a folded-chain configuration. Philos. Mag. 2, 1171 (1957).CrossRefGoogle Scholar
Hoffman, J.D. and Lauritzen, J.I. Jr.: Crystallization of bulk polymers with chain folding: Theory of growth of lamellar spherulites. J. Res. Nat. Bur. Stand. 65A, 297 (1961).CrossRefGoogle ScholarPubMed
Hoffman, J.D.: Theoretical aspects of polymer crystallization with chain folds: Bulk polymers. Soc. Plast. Eng. Trans. 4, 315 (1964).Google Scholar
Hoffman, J.D., Davis, G.T., and Lauritzen, J.I. Jr.: The rate of crystallization of linear polymers with chain folding, in Treatise on Solid State Chemistry, Vol. 3, edited by Hannay, N.B. (Plenum Press, New York, NY, 1976), pp. 497–614.CrossRefGoogle Scholar
Ziabicki, A.: Nucleation-controlled multiphase transitions. J. Chem. Phys. 123, 174103 (2005).CrossRefGoogle ScholarPubMed
Turnbull, D.: Formation of crystal nuclei in liquid metals. J. Appl. Phys. 21, 1022 (1950).CrossRefGoogle Scholar
Frenkel, J.: Kinetic Theory of Liquids (Oxford University Press, London, 1946).Google Scholar
Zeldovich, Y.B.: Theory of formation of a new phase: Cavitation. Acta Phys.Chim. USSR 18, 1 (1943).Google Scholar
Frank, F.C. and Tosi, M.: On the theory of polymer crystallization. Proc. R. Soc. London, Ser. A 263, 323 (1961).Google Scholar
Misztal-Faraj, B. and Ziabicki, A.: Effects of predetermined nuclei and limited transformation on polymorphic crystallization in a model polymer. J. Appl. Polym. Sci. 125, 4243 (2011).CrossRefGoogle Scholar
Monasse, B. and Haudin, J.M.: Growth transition and morphology change in polypropylene. Colloid Polym. Sci. 263, 822 (1985).CrossRefGoogle Scholar
Van Krevelen, D.W.: Properties of polymers (Elsevier, Amsterdam, 2000), pp. 469, 597.Google Scholar
Mark, J.E.: Physical Properties of Polymers Handbook (American Institute of Physics, Woodbury, NY, 1996), p. 424.Google Scholar
Voigt-Martin, I.G. and Mandelkern, L.: A quantitative electron-microscopic study of a linear polyethylene fraction crystallized at different temperature. J. Polym. Sci. 19, 1769–1790 (1981).Google Scholar