Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-02T23:15:29.874Z Has data issue: false hasContentIssue false
  • English
  • Français

A relation between the surface energy and the Debye temperature for cubic solids

Published online by Cambridge University Press:  31 January 2011

V.K. Tewary  and
E.R. Fuller Jr.
V.K. Tewary
Affiliation:
Institute for Materials Science and Engineering, National Institute of Standards and Technology, Gaithersburg, Maryland 20899
E.R. Fuller Jr.
Affiliation:
Institute for Materials Science and Engineering, National Institute of Standards and Technology, Gaithersburg, Maryland 20899
Get access

Abstract

It is shown that a phenomenological relation exists between the Debye temperature θ (in degree Kelvin) and the surface energy Γ (in ergs/cm2) of cubic solids: 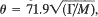, where M is the atomic weight. This relation is derived theoretically in the Debye isotropic approximation by assuming that the interatomic potential is central. No restrictions are imposed on the range of the potential. The relation is obeyed very well by the observed values of θ and Γ in the case of many solids.

Type
Articles
Information
Journal of Materials Research , Volume 5 , Issue 5 , May 1990 , pp. 1118 - 1122
Copyright
Copyright © Materials Research Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Gilman, J.G., J. Appl. Phys. 31, 2208 (1960).CrossRefGoogle Scholar
2Miedema, A.R. and Dorleign, J.W.F., Surf. Sci. 95, 447 (1980).CrossRefGoogle Scholar
3Miedema, A. R. and de Chatel, P. F., Theory of Alloy Phase Formation, edited by Bennett, L.H. (TMS-AIME, Warrendale, PA, 1980), p. 344.Google Scholar
4Mukherjee, K., Phil. Mag. 12, 915 (1965).CrossRefGoogle Scholar
5Tewary, V. K., J. Phys. F (Metal Phys.) 3, 704 (1973).CrossRefGoogle Scholar
6Maradudin, A. A., Montroll, E.W., Weiss, G. H., and Ipatova, I. P., Theory of Lattice Dynamics in the Harmonic Approximation; Solid State Phys. Suppl. (Academic Press, New York, 1971), 2nd ed., Vol. 3.Google Scholar
7Handbook of Materials Science, edited by Lynch, C.T. (C.R.C. Press, Cleveland, OH, 1974).Google Scholar
8Am. Inst. of Phys. Handbook, edited by Gray, D. E. (McGraw-Hill, New York, 1972), 3rd ed.Google Scholar
9Rice, J.R. and Thomson, Robb, Phil. Mag. 29, 73 (1974).CrossRefGoogle Scholar
10Hirth, J. R. and Lothe, J., Theory of Dislocations (Wiley Interscience, New York, 1982), 2nd ed.Google Scholar