Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T05:59:45.035Z Has data issue: false hasContentIssue false
  • English
  • Français

The reduced modulus in the analysis of sharp instrumented indentation tests

Published online by Cambridge University Press:  07 June 2012

Sara A. Rodríguez ,
Jorge Alcalá  and
Roberto M. Souza
Sara A. Rodríguez*
Affiliation:
Research Group of Fatigue and Surfaces, Mechanical Engineering School, Universidad del Valle, Cll 13 No 100-00, Cali, Colombia; and Department of Mechanical Engineering, Surface Phenomena Laboratory, University of São Paulo, 2231 05508-900 São Paulo, Brazil
Jorge Alcalá
Affiliation:
GRICCA-EUETIB, Universitat Politècnica de Catalunya, Barcelona 08036, Spain
Roberto M. Souza
Affiliation:
Department of Mechanical Engineering, Surface Phenomena Laboratory, University of São Paulo, 2231 05508-900 São Paulo, Brazil
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

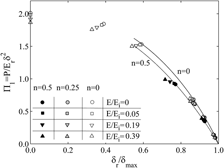
In the analysis of instrumented indentation data, it is common practice to incorporate the combined moduli of the indenter (Ei) and the specimen (E) in the so-called reduced modulus (Er) to account for indenter deformation. Although indenter systems with rigid or elastic tips are considered as equivalent if Er is the same, the validity of this practice has been questioned over the years. The present work uses systematic finite element simulations to examine the role of the elastic deformation of the indenter tip in instrumented indentation measurements and the validity of the concept of the reduced modulus in conical and pyramidal (Berkovich) indentations. It is found that the apical angle increases as a result of the indenter deformation, which influences in the analysis of the results. Based upon the inaccuracies introduced by the reduced modulus approximation in the analysis of the unloading segment of instrumented indentation applied load (P)–penetration depth (δ) curves, a detailed examination is then conducted on the role of indenter deformation upon the dimensionless functions describing the loading stages of such curves. Consequences of the present results in the extraction of the uniaxial stress–strain characteristics of the indented material through such dimensional analyses are finally illustrated. It is found that large overestimations in the assessment of the strain hardening behavior result by neglecting tip compliance. Guidelines are given in the paper to reduce such overestimations.

Keywords

NanoindentationContact mechanicsMechanical propertiesFinite element analysis
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 16 , 28 August 2012 , pp. 2148 - 2160
Copyright
Copyright © Materials Research Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).Google Scholar
2.Dao, M., Chollacoop, N., Van Vliet, K.J., Venkatesh, T.A., and Suresh, S.: Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 49, 3899 (2001).CrossRefGoogle Scholar
3.Casals, O. and Alcalá, J.: The duality in mechanical property extractions from Vickers and Berkovich instrumented indentation experiments. Acta Mater. 53, 3545 (2005).Google Scholar
4.Johnson, K.L.: Contact Mechanics (Cambridge University Press, Cambridge, 1985).Google Scholar
5.Rodríguez, S.A., Souza, R.M., and Alcalá, J.: A critical reassessment of the elastic unloading in sharp instrumented indentation experiments: Mechanical properties extraction. Philos. Mag. 91, 1409 (2011).Google Scholar
6.Chaudhri, M.M.: A note on a common mistake in the analysis of nanoindentation data. J. Mater. Res. 16, 336 (2001).Google Scholar
7.Lim, Y.Y. and Chaudhri, M.M.: Experimental investigations of the normal loading of elastic spherical and conical indenters on to elastic flats. Philos. Mag. 83, 3427 (2003).Google Scholar
8.Jeong, S.M. and Lee, H.L.: Finite element analysis of the tip deformation effect on nanoindentation hardness. Thin Solid Films 492, 173–179 (2005).Google Scholar
9.Ficher-Cripps, A.C.: Use of combined elastic modulus in depth-sensing indentation with a conical indenter. J. Mater. Res. 18, 1043–1045 (2003).Google Scholar
10.Lim, Y.Y. and Chaudhri, M.M.: Indentation of elastic solids with rigid cones. Philos. Mag. 84, 2877–2903 (2004).Google Scholar
11.Choi, I., Kraft, O., and Schwaiger, R.: Validity of the reduced modulus concept to describe indentation loading response for elastoplastic materials with sharp indenters. J. Mater. Res. 24, 998–1006 (2009).Google Scholar
12.Troyon, M. and Huang, L.Y.: Correction factor for contact area in nanoindentation measurements. J. Mater. Res. 20, 610–617 (2005).Google Scholar
13.Veprek-Heijman, M.G.J., Veprek, R.G., Argon, A.S., Parks, D.M., and Veprek, S.: Non-linear finite element constitutive modeling of indentation into super- and ultrahard materials: The plastic deformation of the diamond tip and the ratio of hardness to tensile yield strength of super- and ultrahard nanocomposites. Surf. Coat. Technol. 203, 3385–3391 (2009).Google Scholar
14.McElhaney, K.W., Vlassak, J.J., and Nix, W.D.: Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J. Mater. Res. 13, 1300–1306 (1998).Google Scholar
15.Gong, J., Miao, H., and Peng, Z.: On the contact area for nanoindentation tests with Berkovich indenter: Case study on soda-lime glass. Mater. Lett. 58, 1349–1353 (2004).Google Scholar
16.Cao, Y.P., Dao, M., and Lu, J.: A precise correcting method for the study of the superhard material using nanoindentation tests. J. Mater. Res. 22, 1255–1264 (2007).Google Scholar
17.Love, A.E.H.: Boussinesq’s problem for a rigid cone. Q. J. Math. 10, 161–175 (1939).Google Scholar
18.Sneddon, I.N.: The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47–57 (1965).Google Scholar
19.Bulychev, S.I., Alekhin, V.P., Shorshorov, M.Kh., Ternovskii, A.P., and Shnyrev, G.D.: Determining Young’s modulus from the indenter penetration diagram. Ind. Lab., 41, 1409–1412 (1975).Google Scholar
20.Hay, J.C., Bolshakov, A., and Pharr, G.M.: A critical examination of the fundamental relations used in the analysis of nanoindentation data. J. Mater. Res. 14, 2296–2305 (1999).Google Scholar
21.Rodríguez, S.A., Farias, M.C., and Souza, R.M.: Finite element and dimensional analysis algorithm for the prediction of mechanical properties of bulk materials and thin films. Surf. Coat. Technol. 205, 1386–1392 (2010).Google Scholar
22.Cheng, Y.T. and Cheng, C.M.: Scaling, dimensional analysis, and indentation measurements. Mater. Sci. Eng., R. 44, 91–149 (2004).CrossRefGoogle Scholar
23.Alcalá, J. and Esqué-De Los Ojos, D.: Reassessing spherical indentation: Contact regimes and mechanical property extractions. Int. J. Solids Struct. 47, 2714–2732 (2010).Google Scholar
24.Mata, M. and Alcalá, J.: The role of friction on sharp indentation. J. Mech. Phys. Solids 52, 145 (2004).CrossRefGoogle Scholar
25.Harsono, E., Swaddiwudhipong, S., and Liu, Z.S.: The effect of friction on indentation test results. Modell. Simul. Mater. Sci. Eng. 16, 065001 (2008).Google Scholar
26.Rodríguez, S.A., Farias, M.C., and Souza, R.M.: Analysis of the tip roundness effects on the micro- and macroindentation response of elastic-plastic materials. J. Mater. Res. 24, 1037–1044 (2009).Google Scholar
27.Rodríguez, S.A., Farias, M.C., and Souza, R.M.: Analysis of the effects of conical indentation variables on the indentation response of elastic-plastic materials through factorial design of experiment. J. Mater. Res. 24, 1222–1234 (2009).Google Scholar
28.Mady, C.E.K., Rodríguez, S.A., Gómez, A.G., and Souza, R.M.: Effects of mechanical properties, residual stress and indenter tip geometry on instrumented indentation data in thin films. Surf. Coat. Technol. 205, 1393–1397 (2010).Google Scholar
29.Oliver, W.C. and Pharr, G.M.: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19, 3–20 (2004).Google Scholar
30.Sun, Y., Zheng, S., Bell, T., and Smith, J.: Indenter tip radius and load frame compliance calibration using nanoindentation loading curves. Philos. Mag. Lett. 79, 649–658 (1999).CrossRefGoogle Scholar
31.Cheng, Y.T. and Cheng, C.M.: Relationships between hardness, elastic modulus, and the work of indentation. Appl. Phys. Lett. 73, 614–616 (1998).Google Scholar
32.Cao, Y.P., Qian, X.Q., Lu, J., and Yao, Z.H.: An energy-based method to extract plastic properties of metal materials from conical indentation tests. J. Mater. Res. 20, 1194–1206 (2005).CrossRefGoogle Scholar
33.King, R.B.: Elastic analysis of some punch problems for a layered medium. Int. J. Solids Struct. 23, 1657–1664 (1987).Google Scholar
34.Rodríguez, S.A.: Modelamento do Ensaio de Indentação Instrumentada Usando Elementos Finitos e Análise Dimensional– Análise de Unicidade, Variações Experimentais, Atrito e Geometria e Deformações do Indentador. Ph.D. Thesis, University of São Paulo, São Paulo, Brazil, 2010.Google Scholar
35.Casals, O., Ocenasek, J., and Alcalá, J.: Crystal plasticity finite element simulations of pyramidal indentation in copper single crystals. Acta Mater. 55, 55–68 (2007).Google Scholar
36.Alcalá, J., Esque-De Los Ojos, D., and Rodríguez, S.A.: The role of crystalline anisotropy in mechanical property extractions through Berkovich indentation. J. Mater. Res. 24, 1235–1244 (2009).Google Scholar
37.Rodríguez, S.A., Alcalá, J., and Souza, R.M.: Effects of elastic indenter deformation on spherical instrumented indentation tests: The reduced elastic modulus. Philos. Mag. 91, 7–9 (2010).Google Scholar
38.Mata, M. and Alcalá, J.: Mechanical property evaluation through sharp indentations in elastoplastic and fully plastic contact regimes. J. Mater. Res. 18, 1705–1709 (2003).Google Scholar
39.Casals, O., Alcalá, J., and Očenášek, J.: Micromechanics of pyramidal indentation in fcc metals: Single crystal plasticity finite element analysis. J. Mech. Phys. Solids 56, 3277–3303 (2008).Google Scholar
40.Sakharova, N.A., Fernandes, J.V., Antunes, J.M., and Oliveira, M.C.: Comparison between Berkovich, Vickers and conical indentation tests: A three-dimensional numerical simulation study. Int. J. Solids Struct. 46, 1095–1104 (2009).Google Scholar
41.Swaddiwudhipong, S., Hua, J., Tho, K.K., and Liu, Z.S.: Equivalency of Berkovich and conical load-indentation curves. Modell. Simul. Mater. Sci. Eng. 14, 71–82 (2006).CrossRefGoogle Scholar