Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:49:12.640Z Has data issue: false hasContentIssue false
  • English
  • Français

On the behaviors of porous shape memory alloy beam with gradient porosity under pure bending

Published online by Cambridge University Press:  15 November 2018

Yanan Zhang ,
Bingfei Liu Open the ORCID record for Bingfei Liu [Opens in a new window] ,
Chunzhi Du  and
Rui Zhou
Yanan Zhang
Affiliation:
Airport College, Civil Aviation University of China, Tianjin 300300, China
Bingfei Liu*
Affiliation:
Aeronautical Engineering College, Civil Aviation University of China, Tianjin 300300, China
Chunzhi Du*
Affiliation:
Aeronautical Engineering College, Civil Aviation University of China, Tianjin 300300, China
Rui Zhou
Affiliation:
Aeronautical Engineering College, Civil Aviation University of China, Tianjin 300300, China
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

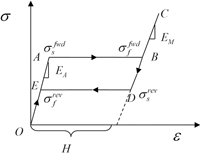
An analytical research is developed using the averaging technique of composites for the macroscopic behaviors of porous shape memory alloy (SMA) beam with different porosity under pure bending. The whole material is regarded as a composite beam of porous SMA and dense SMA, in which the component fractions of the porous SMA show gradient changes over geometric dimension. To get the theoretical solution of such material under pure bending, the Mises yield theory and the ideal elastoplastic model are used to describe the phase transition of the material. The macroscopic behaviors of the porous SMAs beam with different porosity are then simulated using the averaging technique of composites. Examples for a porous SMA beam with gradient porosity from 0 to 50% considering the tension compression asymmetry of the SMAs are then supplied; the results show that after transformation the stress distribution in the whole material is lower than in the case of the pure elastic gradient porous materials, and for different part of the SMA with different porosity shows different strength characters.

Keywords

porous shape memory alloygradient porosityconstitutive model
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 2 , 28 January 2019 , pp. 282 - 289
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Liang, C., Davidson, F., Scjetky, L.M., and Straub, F.K.: Applications of torsional shape memory alloy actuators for active rotor blade control: Opportunities and limitations. In SPIE Proceedings Smart Structures and Materials: Smart Structures and Integrated Systems International Society for Optics and Photonics, Vol. 2717, Chopra, I., ed. (SPIE, Bellingham, 1996); p. 91.Google Scholar
Garner, L.J., Wilson, L.N., Lagoudas, D.C., and Rediniotis, O.K.: Development of a shape memory alloy actuated biomimetic vehicle. Smart Mater. Struct. 9, 673 (2000).CrossRefGoogle Scholar
Shabalovskaya, S.A.: On the nature of the biocompatibility and on medical applications of NiTi shape memory and superelastic alloys. Biomed Mater Eng 6, 267 (1996).Google Scholar
Adini, A.R., Feldman, Y., Cohen, S.R., Rapoport, L., Moshkovich, A., Redlich, M., Moshonov, J., Shay, B., and Tenne, R.: Alleviating fatigue and failure of NiTi endodontic files by a coating containing inorganic fullerene-like WS2 nanoparticles. J. Mater. Res. 26, 1234 (2011).CrossRefGoogle Scholar
Martynova, I., Skorohod, V., Solonin, S., and Goncharuk, S.: Shape memory and superelasticity behaviour of porous Ti–Ni material. J. Phys. IV 01, 421 (1991).Google Scholar
Gyunter, V.E., Sysoliatin, P., and Temerkahamor, T.: Superelastic Shape Memory Implants in Maxillofacial Surgery, Traumatology, Orthopedics, and Neurosurgery (Tomsk university publishing house, Tomsk, 1995).Google Scholar
Bansiddhi, A. and Dunand, D.C.: Shape-memory NiT–Nb foams. J. Mater. Res. 24, 2107 (2009).CrossRefGoogle Scholar
Qidwai, M.A., Entchrv, P.B., Lagoudas, D.C., and DeGiorgi, V.G.: Modeling of the thermomechanical behavior of porous shape memory alloys. Int. J. Solids Struct. 38, 8653 (2001).CrossRefGoogle Scholar
Entchev, P.B. and Lagoudas, D.C.: Modeling porous shape memory alloys using micromechanical averaging techniques. Mech. Mater. 34, 1 (2002).CrossRefGoogle Scholar
Entchev, P.B. and Lagoudas, D.C.: Modeling of transformation induced plasticity and its effect on the behavior of porous shape memory alloys. Part II: Porous SMA response. Mech. Mater. 36, 893 (2004).CrossRefGoogle Scholar
Li, B-Y., Rong, L-J., and Li, Y-Y.: Porous NiTi alloy prepared from elemental powder sintering. J. Mater. Res. 13, 2847 (1998).CrossRefGoogle Scholar
Liu, B-F., Dui, G-S., and Zhu, Y-P.: On phase transformation behavior of porous shape memory alloy. J. Mech. Behav. Biomed. Mater. 5, 9 (2012).CrossRefGoogle Scholar
Li, Y-H., Rong, L-J., and Li, Y-Y.: Pore characteristics of porous NiTi alloy fabricated by combustion synthesis. J. Alloys Compd. 325, 259 (2001).CrossRefGoogle Scholar
Sepe, V., Auricchio, F., Marfia, S., and Sacco, E.: Micromechanical analysis of porous SMA. Smart Mater. Struct. 24, 085035 (2015).CrossRefGoogle Scholar
Yuan, B., Chung, C-Y., Zhang, Y-P., Zeng, M-Q., and Zhu, M.: Control of porosity and superelasticity of porous NiTi shape memory alloys prepared by hot isostatic pressing. Smart Mater. Struct. 14, S201 (2005).CrossRefGoogle Scholar
Zhang, Y-P., Li, X-P., and Zhang, X-P.: Gradient porosity and large pore size NiTi shape memory alloys. Scr. Mater. 57, 1020 (2007).CrossRefGoogle Scholar
Xiong, J-Y., Li, Y-C., Hodgson, P.D., and Wen, C.: Influence of porosity on shape memory behavior of porous NiTi shape memory alloy. Funct. Mater. Lett. 1, 215 (2008).CrossRefGoogle Scholar
Li, D-S., Zhang, Y-P., Eggeler, G., and Zhang, X-P.: High porosity and high-strength porous NiTi shape memory alloys with controllable pore characteristics. J. Alloys Compd. 470, L1 (2009).CrossRefGoogle Scholar
Zhou, D., Gao, Y., Lai, M., Li, H., Yuan, B., and Zhu, M.: Fabrication of NiTi shape memory alloy with graded porosity to imitate human long-bone structure. J. Bionic Eng. 12, 575 (2015).CrossRefGoogle Scholar
Sharma, N., Kumar, K., Raj, T., and Kumar, V.: Porosity exploration of SMA by Taguchi, regression analysis and genetic programming. J. Intell. Manuf. 5, 1 (2016).Google Scholar
Li, Z., Zhang, L., Meng, Z., He, Z., Zhang, Y., and Jiang, Y.: Microstructure evolution and mechanical properties of porous surface NiTi gradient alloy prepared by spark plasma sintering. Rare Metal Mater. Eng. 47, 371 (2018).Google Scholar
Fousová, M., Vojtěch, D., Kubásek, J., Jablonská, E., and Fojt, J.: Promising characteristics of gradient porosity Ti–6Al–4V alloy prepared by SLM process. J. Mech. Behav. Biomed. Mater. 69, 368 (2017).CrossRefGoogle ScholarPubMed
Xue, L-J., Dui, G-S., Liu, B-F., and Xin, L-B.: A phenomenological constitutive model for functionally graded porous shape memory alloy. Int. J. Eng. Sci. 78, 103 (2014).CrossRefGoogle Scholar
Zhao, Y., Taya, M., Kang, Y-S., and Kawasaki, A.: Compression behavior of porous Ni–Ti shape memory alloy. Acta Mater. 53, 337 (2005).CrossRefGoogle Scholar
Entchev, P.B. and Lagoudas, D.C.: Modeling of transformation induced plasticity and its effect on the behavior of porous shape memory alloys. Part I: Constitutive model for fully dense SMAs. Mech. Mater. 36, 865 (2004).CrossRefGoogle Scholar