Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T10:26:14.007Z Has data issue: false hasContentIssue false
  • English
  • Français

A new exponential function to represent the effect of grain size on the strength of pure iron over multiple length scales

Published online by Cambridge University Press:  03 July 2019

K.S. Ravi Chandran
K.S. Ravi Chandran*
Affiliation:
Department of Metallurgical Engineering, The University of Utah, Salt Lake City, Utah 84112, USA
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

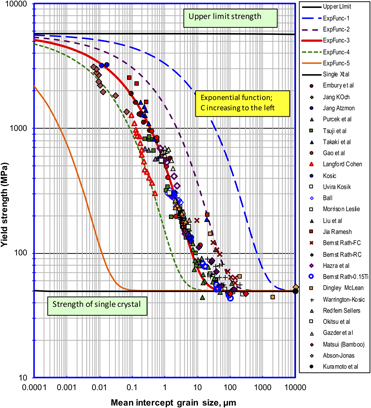
A rigorous analysis of yield strength of pure iron over a wide grain size scale, using an extensive compilation of experimental data, indicates that the common Hall–Petch relationship is not obeyed with large deviations at the extremes of grain size. The author proposes here a phenomenological exponential function to represent the grain size effect on strength over multiple length scales. It is shown that the exponential function describes the grain size dependence of strength remarkably well, on the basis of a large set of experimental data for pure Fe. A nonlinear regression analysis indicated that the function provided a very high degree of correlation of data. The validity of the function is also supported by its conformation to physical boundary conditions at the extremes of grain size, that is, by asymptotically reaching the limiting stress for dislocation nucleation at infinitesimal grain size, and, the strength of single crystal at infinite grain size. The exponential form is a significant improvement over the Hall–Petch relationship and may be used as a guide to develop a reliable theory of grain size strengthening of iron.

Keywords

grain sizeFestrength
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 13: Focus Issue: Intrinsic and Extrinsic Size Effects in Materials , 15 July 2019 , pp. 2315 - 2324
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Hall, E.O.: The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. B 64, 747–753 (1951).CrossRefGoogle Scholar
Petch, N.J.: The cleavage strength of polycrystals. J. Iron Steel Inst. 174, 25–28 (1953).Google Scholar
Armstrong, R.W.: The influence of polycrystal grain size on several mechanical properties of materials. Metall. Trans. 1, 1169–1176 (1970).CrossRefGoogle Scholar
Armstrong, R.W.: 60 years of Hall–Petch: Past to present nano-scale connections. Mater. Trans. 55, 2–12 (2014).CrossRefGoogle Scholar
Hansen, N.: Polycrystalline strengthening. Metall. Trans. A 16, 2167–2190 (1985).CrossRefGoogle Scholar
Cottrell, A.H.: Theory of brittle fracture in steel and similar metals. Trans. Metall. Soc. AIME 212, 192 (1958).Google Scholar
Li, J.C.M.: Petch relation and grain boundary sources. Trans. Metall. Soc. AIME 227, 239–247 (1963).Google Scholar
Anderson, E., Law, D., King, W., and Spreadborough, J.: The relationship between lower yield stress and grain size in Armco iron. Trans. Metall. Soc. AIME 242, 115–119 (1968).Google Scholar
Lesuer, D.R., Syn, C.K., and Sherby, O.D.: Nano-scale strengthening from grains, subgrains, and particles in Fe-based alloys. J. Mater. Sci. 45, 4889–4894 (2010).CrossRefGoogle Scholar
Petch, N.J.: The upper yield stress of polycrystalline iron. Acta Metall. 12, 59–65 (1964).CrossRefGoogle Scholar
Embury, J.D., Keh, S., and Fisher, R.M.: Substructural strengthening in materials subject to large plastic strains. Trans. Metall. Soc. AIME 236, 1252–1260 (1966).Google Scholar
Jang, J.S. and Koch, C.C.: The Hall–Petch relationship in nanocrystalline iron produced by ball milling. Scr. Metall. Mater. 24, 1599–1604 (1990).CrossRefGoogle Scholar
Jang, D. and Atzmon, M.: Grain-size dependence of plastic deformation in nanocrystalline Fe. J. Appl. Phys. 93, 9282–9286 (2003).CrossRefGoogle Scholar
Purcek, G., Saray, O., Karaman, I., and Maier, H.J.: High strength and high ductility of ultrafine-grained, interstitial-free steel produced by ECAE and annealing. Metall. Mater. Trans. A 43, 1884–1894 (2012).CrossRefGoogle Scholar
Tsuji, N., Ito, Y., Saito, Y., and Minamino, Y.: Strength and ductility of ultra-fine-grained aluminum and iron produced by ARB and annealing. Scr. Mater. 47, 893–899 (2002).CrossRefGoogle Scholar
Takaki, S., Kawasaki, K., and Kimura, Y.: Mechanical properties of ultra-fine-grained steels. J. Mater. Process. Technol. 117, 359–363 (2001).CrossRefGoogle Scholar
Gao, S., Chen, M., Chen, S., Kamikawa, N., Shibata, A., and Tsuji, N.: Yielding behavior and its effect on uniform elongation of fine grained IF steel. Mater. Trans. 55, 73–77 (2014).CrossRefGoogle Scholar
Langford, G. and Cohen, M.: Strain hardening of iron by severe plastic deformation. ASM Trans. Q. 62, 623–638 (1969).Google Scholar
Kosik, O., Abson, D.J., and Jonas, J.J.: Strengthening effect of hot-working subgrains at room temperature. J. Iron Steel Inst. 209, 624–629 (1971).Google Scholar
Ball, C.J.: The texture and mechanical properties of iron. J. Iron Steel Inst. 191, 232–236 (1959).Google Scholar
Liu, C.T., Armstrong, R.W., and Gurland, J.: Determination of the fractional stress for polycrystalline iron and carbon steels from their stress–strain behavior and their grain-size dependence. J. Iron Steel Inst. 209, 142–146 (1971).Google Scholar
Jia, D., Ramesh, K.T., and Ma, E.: Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron. Acta Mater. 51, 3495–3509 (2003).CrossRefGoogle Scholar
Morrison, W.B. and Leslie, W.C.: The yield stress-grain size relation in iron substitutional alloys. Metall. Trans. 4, 379–381 (1973).CrossRefGoogle Scholar
Bernstein, I.M. and Rath, B.B.: The role of grain boundary solutes and structure on the yielding and intergranular cracking of iron. Metall. Trans. 4, 1545–1551 (1973).Google Scholar
Hazra, S., Pereloma, E.V., and Gazder, A.A.: Microstructure and mechanical properties after annealing of equal-channel angular pressed interstitial-free steel. Acta Mater. 59, 4015–4029 (2011).CrossRefGoogle Scholar
Dingley, D.J. and McLean, D.: Components of the flow stress of iron. Acta Metall. 15, 885–901 (1967).CrossRefGoogle Scholar
Okitsu, Y., Takata, N., and Tsuji, N.: Dynamic deformation behavior of ultrafine-grained iron produced by ultrahigh strain deformation and annealing. Scr. Mater. 64, 896–899 (2011).CrossRefGoogle Scholar
Gazder, A., Cao, W., Davies, C.H., and Pereloma, E.V.: An EBSD investigation of interstitial-free steel subjected to equal channel angular extrusion. Mater. Sci. Eng., A 497, 341–352 (2008).CrossRefGoogle Scholar
Matsui, H., Moriya, S., Takaki, S., and Kimura, H.: Mechanical properties of high purity iron at low temperatures. Trans. Jpn. Inst. Met. 19, 163–170 (1978).CrossRefGoogle Scholar
Abson, D.J. and Jonas, J.J.: The Hall–Petch relation and high-temperature subgrains. Met. Sci. J. 4, 24–28 (1970).CrossRefGoogle Scholar
Kuramoto, E., Aono, Y., and Kitajima, K.: Thermally activated slip deformation of high purity iron single crystals between 4.2 K and 300 K. Scr. Metall. 13, 1039–1042 (1979).CrossRefGoogle Scholar
Hull, D.: Introduction to Dislocations, 2nd ed. (Pergamon Press, Oxford, 1975).Google Scholar
Cottrell, A.H.: Dislocations and Plastic Flow in Crystals, 1st ed. (Clarendon Press, Oxford, 1953).Google Scholar
Lucon, E., Abiko, K., Lambrecht, M., and Rehmer, B.: Tensile properties of commercially pure, high-purity and ultra-high-purity iron: Results of an international round robin; NIST Tech. Note 1879; National Institute of Standards and Technology, US Department of Commerce: DC, 2015.Google Scholar
Baldwin, W.M.: Yield strength of metals as a function of grain size. Acta Metall. 6, 139–141 (1958).CrossRefGoogle Scholar
Christman, T.: Grain boundary strengthening exponent in conventional and ultrafine microstructures. Scr. Metall. Mater. 28, 1495–1500 (1993).CrossRefGoogle Scholar
Young, C.M. and Sherby, O.D.: Sub-grain formation and sub-grain-boundary strengthening in Fe-based materials. J. Iron Steel Inst. 211, 640–647 (1973).Google Scholar
Gertsman, V., Hoffmann, M., Gleiter, H., and Birringer, R.: The study of grain size dependence of yield stress of copper for a wide grain size range. Acta Metall. Mater. 42, 3539–3544 (1994).CrossRefGoogle Scholar
Hansen, N.: Hall–Petch relation and boundary strengthening. Scr. Mater. 51, 801–806 (2004).CrossRefGoogle Scholar
Dunstan, D.J. and Bushby, A.J.: Grain size dependence of the strength of metals: The Hall–Petch effect does not scale as the inverse square root of grain size. Int. J. Plast. 53, 56–65 (2014).CrossRefGoogle Scholar
Cordero, Z.C., Knight, B.E., and Schuh, C.A.: Six decades of the Hall–Petch effect—A survey of grain-size strengthening studies on pure metals. Int. Mater. Rev. 61, 495–512 (2016).CrossRefGoogle Scholar
Suryanarayana, C., Mukhopadhyay, D., Patankar, S.N., and Froes, F.H.: Grain size effects in nanocrystalline materials. J. Mater. Res. 7, 2114–2118 (1992).CrossRefGoogle Scholar
Nieh, T.G. and Wadsworth, J.: Hall–Petch relation in nanocrystalline solids. Scr. Metall. Mater. 25, 955–958 (1991).CrossRefGoogle Scholar
Pande, C.S. and Cooper, K.P.: Nanomechanics of Hall–Petch relationship in nanocrystalline materials. Prog. Mater. Sci. 54, 689–706 (2009).CrossRefGoogle Scholar
Murr, L.E.: Some observations of grain boundary ledges and ledges as dislocation sources in metals and alloys. Metall. Trans. A 6, 505–515 (1975).CrossRefGoogle Scholar
Murr, L.E.: Yielding and grain-boundary ledges: Some comments on the Hall–Petch relation. Appl. Phys. Lett. 24, 533–536 (1974).CrossRefGoogle Scholar
Kumar, K.S., Suresh, S., Chisholm, M.F., Horton, J.A., and Wang, P.: Deformation of electrodeposited nanocrystalline nickel. Acta Mater. 51, 387–405 (2003).CrossRefGoogle Scholar
Murr, L.E.: Dislocation ledge sources: Dispelling the myth of frank–read source importance. Metall. Mater. Trans. A 47, 5811–5826 (2016).CrossRefGoogle Scholar
Van Swygenhoven, H., Derlet, P.M., and Froseth, A.G.: Nucleation and propagation of dislocations in nanocrystalline fcc metals. Acta Mater. 54, 1975–1983 (2006).CrossRefGoogle Scholar
Van Swygenhoven, H., Derlet, P.M., and Hasnaoui, A.: Atomic mechanism for dislocation emission from nanosized grain boundaries. Phys. Rev. B 66, 024101 (2002).CrossRefGoogle Scholar
Asaro, R.J. and Suresh, S.: Mechanistic models for the activation volume and rate sensitivity in metals with nanocrystalline grains and nano-scale twins. Acta Mater. 53, 3369–3382 (2005).CrossRefGoogle Scholar
Misra, A., Hirth, J.P., and Hoagland, R.G.: Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites. Acta Mater. 53, 4817–4824 (2005).CrossRefGoogle Scholar
Meyers, M.A. and Ashworth, E.: A model for the effect of grain size on the yield stress of metals. Philos. Mag. A 46, 737–759 (1982).CrossRefGoogle Scholar
Fu, H-H., Benson, D.J., and Meyers, M.A.: Analytical and computational description of effect of grain size on yield stress of metals. Acta Mater. 49, 2567–2582 (2001).CrossRefGoogle Scholar
Chokshi, A.H., Rosen, A., Karch, J., and Gleiter, H.: On the validity of the Hall–Petch relationship in nanocrystalline materials. Scr. Metall. 23, 1679–1683 (1989).CrossRefGoogle Scholar
Weertman, J.R.: Hall–Petch strengthening in nanocrystalline metals. Mater. Sci. Eng., A 166, 161–167 (1993).CrossRefGoogle Scholar
Meyers, M.A., Mishra, A., and Benson, D.J.: Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 51, 427–556 (2006).CrossRefGoogle Scholar