Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T00:40:18.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of interfacial properties on the viscoelastic relaxation of hard–soft block copolymers using finite element analysis

Published online by Cambridge University Press:  08 July 2020

Min Zhang ,
Xiaolin Li ,
Yixing Wang ,
Wei Chen  and
Catherine Brinson
Min Zhang
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois60208, USA Department of Mechanical Engineering and Materials Science, Duke University, Durham, North Carolina27708, USA
Xiaolin Li
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois60208, USA
Yixing Wang
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois60208, USA
Wei Chen
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois60208, USA
Catherine Brinson*
Affiliation:
Department of Mechanical Engineering and Materials Science, Duke University, Durham, North Carolina27708, USA
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

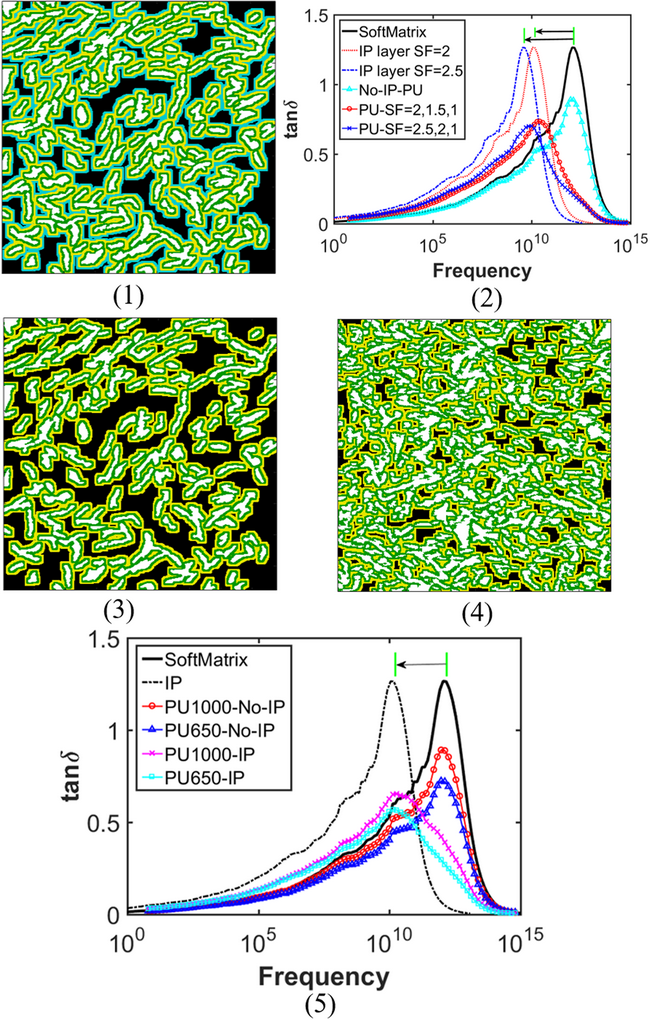
In this paper, we use finite element analysis (FEA) to study the linear viscoelastic response of polyurea, a type of hard–soft block copolymer. A Niblack's algorithm-based technique employed on atomic force microscopy images provides geometry inputs for the FEA model, while the viscoelastic master curves of the soft matrix are obtained via a combination of dynamic mechanical analysis data and molecular dynamic (MD) estimations. In this microstructural image-based FEA framework, we introduce an interphase area of altered properties between the hard and soft domains. Both spatial and property distributions of this interphase area affect the viscoelastic response of the copolymer system. To quantitatively investigate the impact of structural and property features of the interphase on the energy storage and dissipation of a system during linear perturbation, we develop a statistical descriptor representation of the interphase region related to physical parameters. Utilizing decision-tree and random forest concepts from machine learning, we apply a ranking algorithm to identify the most significant features for four different mechanical response descriptors. Results show that the total interphase volume fraction and shifting factor distributions in the interphase area dominate the magnitude of the tan δ peak, whereas the magnitudes of the shifting factors primarily affect the tan δ peak location in frequency space. This method allows us to readily identify the dominant features impacting individual properties and paves the way for material design of hard–soft block copolymer systems.

Keywords

polymerviscoelasticityinterphase
Type
Article
Information
Journal of Materials Research , Volume 35 , Issue 14 , 28 July 2020 , pp. 1857 - 1873
Check for updates
Copyright
Copyright © Materials Research Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Das, S., Cox, D.F., Wilkes, G.L., Klinedinst, D.B., Yilgor, I., Yilgor, E., and Beyer, F.L.: Effect of symmetry and H-bond strength of hard segments on the structure-property relationships of segmented, nonchain extended polyurethanes and polyureas. J. Macromol. Sci., Part B: Phys. 46(5), 853–875 (2007).CrossRefGoogle Scholar
Grujicic, M., Pandurangan, B., King, A.E., Runt, J., Tarter, J., and Dillon, G.: Multi-length scale modeling and analysis of microstructure evolution and mechanical properties in polyurea. J. Mater. Sci. 46(6), 1767–1779 (2011).CrossRefGoogle Scholar
Seefried, C.G., Koleske, J.V., and Critchfield, F.E.: Thermoplastic urethane elastomers 2. Effects of variations in hard-segment concentration. J. Appl. Polym. Sci. 19(9), 2503–2513 (1975).CrossRefGoogle Scholar
Rinaldi, R.G., Boyce, M.C., Weigand, S.J., Londono, D.J., and Guise, M.W.: Microstructure evolution during tensile loading histories of a polyurea. J. Macromol. Sci., Part B: Phys. 49(23), 1660–1671 (2011).Google Scholar
Cho, J. and Daniel, I.M.: Reinforcement of carbon/epoxy composites with multi-wall carbon nanotubes and dispersion enhancing block copolymers. Scr. Mater. 58(7), 533–536 (2008).CrossRefGoogle Scholar
Coleman, J.N., Khan, U., and Gun'ko, Y.K.: Mechanical reinforcement of polymers using carbon nanotubes. Adv. Mater. 18(6), 689–706 (2006).CrossRefGoogle Scholar
Cadek, M., Coleman, J., Barron, V., Hedicke, K., and Blau, W.: Morphological and mechanical properties of carbon-nanotube-reinforced semicrystalline and amorphous polymer composites. Appl. Phys. Lett. 81(27), 5123–5125 (2002).CrossRefGoogle Scholar
Roe, R.J. and Zin, W.C.: Phase equilibria and transition in mixtures of a homopolymer and a block copolymer. 2. Phase diagram. Macromolecules 17(2), 189–194 (1984).CrossRefGoogle Scholar
Brinson, L. and Knauss, W.: Thermorheologically complex behavior of multi-phase viscoelastic materials. J. Mech. Phys. Solids 39(7), 859–880 (1991).CrossRefGoogle Scholar
Putz, K.W., Mitchell, C.A., Krishnamoorti, R., and Green, P.F.: Elastic modulus of single-walled carbon nanotube/poly (methyl methacrylate) nanocomposites. J. Macromol. Sci., Part B: Phys. 42(12), 2286–2293 (2004).Google Scholar
Schadler, L., Brinson, L., and Sawyer, W.: Polymer nanocomposites: A small part of the story. JOM 59(3), 53–60 (2007).CrossRefGoogle Scholar
Ramanathan, T., Abdala, A.A., Stankovich, S., Dikin, D.A., Herrera-Alonso, M., Piner, R.D., Adamson, D.H., Schniepp, H.C., Chen, X., Ruoff, R.S., Nguyen, S.T., Aksay, I.A., Prud'Homme, R.K., and Brinson, L.C.: Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 3, 327 (2008).CrossRefGoogle ScholarPubMed
Deng, H., Liu, Y., Gai, D.H., Dikin, D.A., Putz, K.W., Chen, W., Brinson, L.C., Burkhart, C., Poldneff, M., Jiang, B., and Papakonstantopoulos, G.J.: Utilizing real and statistically reconstructed microstructures for the viscoelastic modeling of polymer nanocomposites. Compos. Sci. Technol. 72(14), 1725–1732 (2012).CrossRefGoogle Scholar
Grujicic, M., Pandurangan, B., Bell, W.C., Cheeseman, B.A., Yen, C.F., and Randow, C.L.: Molecular-level simulations of shock generation and propagation in polyurea. Mater. Sci. Eng., A 528(10–11), 3799–3808 (2011).CrossRefGoogle Scholar
Grujicic, M., Yavari, R., Snipes, J.S., Ramaswami, S., Runt, J., Tarter, J., and Dillon, G.: Molecular-level computational investigation of shock-wave mitigation capability of polyurea. J. Mater. Sci. 47(23), 8197–8215 (2012).CrossRefGoogle Scholar
Arman, B., Reddy, A.S., and Arya, G.: Viscoelastic properties and shock response of coarse-grained models of multiblock versus diblock copolymers: Insights into dissipative properties of polyurea. Macromolecules 45(7), 3247–3255 (2012).CrossRefGoogle Scholar
Grujicic, M., Snipes, J.S., Ramaswami, S., Yavari, R., Runt, J., Tarter, J., and Dillon, G.: Coarse-grained molecular-level analysis of polyurea properties and shock-mitigation potential. J. Mater. Eng. Perform. 22(7), 1964–1981 (2013).CrossRefGoogle Scholar
Cui, Z.W. and Brinson, L.C.: Thermomechanical properties and deformation of coarse-grained models of hard-soft block copolymers. Phys. Rev. E 88(2), 10 (2013).CrossRefGoogle ScholarPubMed
Amirkhizi, A.V., Isaacs, J., McGee, J., and Nemat-Nasser, S.: An experimentally-based viscoelastic constitutive model for polyurea, including pressure and temperature effects. Philos. Mag. 86(36), 5847–5866 (2006).CrossRefGoogle Scholar
Grujicic, M., Bell, W.C., Pandurangan, B., and He, T.: Blast-wave impact-mitigation capability of polyurea when used as helmet suspension-pad material. Mater. Des. 31(9), 4050–4065 (2010).CrossRefGoogle Scholar
Xue, L., Mock, W., and Belytschko, T.: Penetration of DH-36 steel plates with and without polyurea coating. Mech. Mater. 42(11), 981–1003 (2010).CrossRefGoogle Scholar
Mohotti, D., Ngo, T., Raman, S.N., Ali, M., and Mendis, P.: Plastic deformation of polyurea coated composite aluminium plates subjected to low velocity impact. Mater. Des. 56, 696–713 (2014).CrossRefGoogle Scholar
Li, Y., Huang, Y., Krentz, T., Natarajan, B., Neely, T., and Schadler, L.S.: Polymer nanocomposite interfaces: The hidden Lever for optimizing performance in spherical nanofilled polymers. In Interface/Interphase in Polymer Nanocomposites, Netravali, A.N. and Mittal, K.L., eds. (Scrivener Publishing LLC, Beverly, MA, 2016).Google Scholar
Cheng, X., Putz, K.W., Wood, C.D., and Brinson, L.C.: Characterization of local elastic modulus in confined polymer films via AFM indentation. Macromol. Rapid Commun. 36(4), 391–7 (2015).CrossRefGoogle ScholarPubMed
Brune, P.F., Blackman, G.S., Diehl, T., Meth, J.S., Brill, D., Tao, Y., and Thornton, J.: Direct measurement of rubber interphase stiffness. Macromolecules 49(13), 4909–4922 (2016).CrossRefGoogle Scholar
Askar, S. and Torkelson, J.M.: Stiffness of thin, supported polystyrene films: Free-surface, substrate, and confinement effects characterized via self-referencing fluorescence. Polymer 99, 417–426 (2016).CrossRefGoogle Scholar
Zhang, M., Askar, S., Torkelson, J.M., and Brinson, L.C.: Stiffness gradients in glassy polymer model nanocomposites: Comparisons of quantitative characterization by fluorescence spectroscopy and atomic force microscopy. Macromolecules 50(14), 5447–5458 (2017).CrossRefGoogle Scholar
Fisher, F. and Brinson, L.: Viscoelastic interphases in polymer–matrix composites: Theoretical models and finite-element analysis. Compos. Sci. Technol. 61(5), 731–748 (2001).CrossRefGoogle Scholar
Wang, Y., Zhang, Y., Zhao, H., Li, X., Huang, Y., Schadler, L.S., Chen, W., and Brinson, L.C.: Identifying interphase properties in polymer nanocomposites using adaptive optimization. Compos. Sci. Technol. 162, 146–155 (2018).CrossRefGoogle Scholar
Garnett, J.C.M.: Colors in material glasses and metal films. Trans. Roy. Soc. 53, 385 (1904).Google Scholar
Bruggeman, D.A.G.: Calculation of various physics constants in heterogenous substances. I. Dielectricity constants and conductivity of mixed bodies from isotropic substances. Ann. Phys. 24(7), 636–664 (1935).CrossRefGoogle Scholar
Lichtenecker, K.: Dielectric constant of natural and synthetic mixtures. Phys. Z 27, 115 (1926).Google Scholar
Hashin, Z. and Shtrikman, S.: A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 11(2), 127–140 (1963).CrossRefGoogle Scholar
Xu, H., Greene, M.S., Deng, H., Dikin, D., Brinson, C., Liu, W.K., Burkhart, C., Papakonstantopoulos, G., Poldneff, M., and Chen, W.: Stochastic reassembly strategy for managing information complexity in heterogeneous materials analysis and design. J. Mech. Des. 135(10), 101010 (2013).CrossRefGoogle Scholar
Hill, R.: Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 11(5), 357–372 (1963).CrossRefGoogle Scholar
Qiao, R. and Catherine Brinson, L.: Simulation of interphase percolation and gradients in polymer nanocomposites. Compos. Sci. Technol. 69(3), 491–499 (2009).CrossRefGoogle Scholar
Qiao, R., Deng, H., Putz, K.W., and Brinson, L.C.: Effect of particle agglomeration and interphase on the glass transition temperature of polymer nanocomposites. J. Polym. Sci., Part B: Polym. Phys. 49(10), 740–748 (2011).CrossRefGoogle Scholar
Xu, H., Li, Y., Brinson, C., and Chen, W.: A descriptor-based design methodology for developing heterogeneous microstructural materials system. J. Mech. Des. 136(5), 051007 (2014).CrossRefGoogle Scholar
Castagna, A.M., Pangon, A., Choi, T., Dillon, G.P., and Runt, J.: The role of soft segment molecular weight on microphase separation and dynamics of bulk polymerized polyureas. Macromolecules 45(20), 8438–8444 (2012).CrossRefGoogle Scholar
Kapur, J.N., Sahoo, P.K., and Wong, A.K.C.: A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 29(3), 273–285 (1985).CrossRefGoogle Scholar
Weszka, J.S., Nagel, R.N., and Rosenfeld, A.: A threshold selection technique. IEEE Trans. Comput. 23(12), 1322–1326 (1974).CrossRefGoogle Scholar
Niblack, W.: An Introduction to Digital Image Processing (Strandberg Publishing Company, Birkeroed, Denmark, 1985), pp. 215.Google Scholar
Khurshid, K., Siddiqi, I., Faure, C., and Vincent, N.: Comparison of Niblack inspired binarization methods for ancient documents. In IS&T/SPIE Electronic Imaging (SPIE, 2009); p. 9.CrossRefGoogle Scholar
Li, X., Zhang, Y., Zhao, H., Burkhart, C., Brinson, L.C., and Chen, W.: A transfer learning approach for microstructure reconstruction and structure-property predictions. Sci. Rep. 8(1), 13461 (2018).CrossRefGoogle ScholarPubMed
Abaqus, D. S.. (2017). Retrieved from: http://www.3ds.com/productsservices/simulia/products/abauqs/.Google Scholar
Qiao, J., Amirkhizi, A.V., Schaaf, K., Nemat-Nasser, S., and Wu, G.: Dynamic mechanical and ultrasonic properties of polyurea. Mech. Mater. 43(10), 598–607 (2011).CrossRefGoogle Scholar
Jia, Z., Amirkhizi, A.V., Nantasetphong, W., and Nemat-Nasser, S.: Experimentally-based relaxation modulus of polyurea and its composites. Mech. Time Dep. Mater. 20(2), 155–174 (2016).CrossRefGoogle Scholar
Zhang, M., Cui, Z., and Catherine Brinson, L.: Mechanical properties of hard–soft block copolymers calculated from coarse-grained molecular dynamics models. J. Polym. Sci., Part B: Polym. Phys. 56(23), 1552–1566 (2018).CrossRefGoogle Scholar
Smith, J.S., Bedrov, D., and Smith, G.D.: A molecular dynamics simulation study of nanoparticle interactions in a model polymer-nanoparticle composite. Compos. Sci. Technol. 63(11), 1599–1605 (2003).CrossRefGoogle Scholar
Smith, G.D., Bedrov, D., Li, L.W., and Byutner, O.: A molecular dynamics simulation study of the viscoelastic properties of polymer nanocomposites. J. Chem. Phys. 117(20), 9478–9489 (2002).CrossRefGoogle Scholar
Starr, F.W., Schrøder, T.B., and Glotzer, S.C.: Molecular dynamics simulation of a polymer melt with a nanoscopic particle. Macromolecules 35(11), 4481–4492 (2002).CrossRefGoogle Scholar
Wei, C., Srivastava, D., and Cho, K.: Thermal expansion and diffusion coefficients of carbon nanotube-polymer composites. Nano Lett. 2(6), 647–650 (2002).CrossRefGoogle Scholar
Park, C.H., Kim, J.H., Ree, M., Sohn, B.-H., Jung, J.C., and Zin, W.-C.: Thickness and composition dependence of the glass transition temperature in thin random copolymer films. Polymer 45(13), 4507–4513 (2004).CrossRefGoogle Scholar
Eitan, A., Fisher, F.T., Andrews, R., Brinson, L.C., and Schadler, L.S.: Reinforcement mechanisms in MWCNT-filled polycarbonate. Compos. Sci. Technol. 66(9), 1162–1173 (2006).CrossRefGoogle Scholar
Li, L., Marrou, S.R., and Torkelson, J.M.: Remarkable glass transition breadths up to 120K exhibited by block-gradient copolymers and by gradient copolymers plasticized by oligomer. Polymer 151, 145–153 (2018).CrossRefGoogle Scholar
Li, X., Zhang, M., Wang, Y., Zhang, M., Prasad, A., Chen, W., Schadler, L., and Brinson, L.C.: Rethinking interphase representations for modeling viscoelastic properties for polymer nanocomposites. Materialia 6, 100277 (2019).CrossRefGoogle Scholar
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001).CrossRefGoogle Scholar
Hasanabadi, A., Baniassadi, M., Abrinia, K., Safdari, M., and Garmestani, H.: 3D microstructural reconstruction of heterogeneous materials from 2D cross sections: A modified phase-recovery algorithm. Comput. Mater. Sci. 111, 107–115 (2016).CrossRefGoogle Scholar
Supplementary material: PDF

Zhang et al. supplementary material

Zhang et al. supplementary material

Download Zhang et al. supplementary material(PDF)
PDF 412.5 KB