Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T13:01:30.309Z Has data issue: false hasContentIssue false
  • English
  • Français

High-throughput measurements of interdiffusivity matrices in face centered cubic Ni–Al–Mo alloys at 1273–1473 K

Published online by Cambridge University Press:  13 February 2017

Shiyi Wen Open the ORCID record for Shiyi Wen [Opens in a new window] ,
Ying Tang ,
Jing Zhong ,
Lijun Zhang ,
Yong Du  and
Feng Zheng
Shiyi Wen
Affiliation:
School of Materials Science and Engineering, Central South University, Changsha, Hunan 410083, People’s Republic of China; and State Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, People’s Republic of China
Ying Tang
Affiliation:
Thermo-Calc Software AB, SE–113 64 Stockholm, Sweden
Jing Zhong
Affiliation:
State Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, People’s Republic of China
Lijun Zhang*
Affiliation:
State Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, People’s Republic of China
Yong Du*
Affiliation:
State Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, People’s Republic of China
Feng Zheng
Affiliation:
School of Materials Science and Engineering, Central South University, Changsha, Hunan 410083, People’s Republic of China
*
a) Address all correspondence to this author. e-mail: [email protected], [email protected]
Get access

Abstract

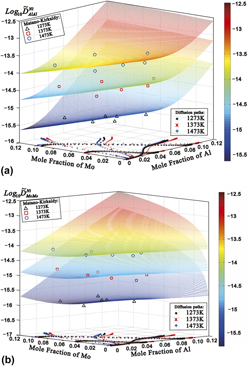
Based on 15 diffusion couples located in face centered cubic single-phase region of ternary Ni–Al–Mo system, high-throughput determination of composition-dependent interdiffusivity matrices at 1273, 1373, and 1473 K was performed by using the recently developed numerical inverse method. The determined main interdiffusivities over the investigated composition and temperature ranges are all positive, and $\tilde D_{{\rm{AlAl}}}^{{\rm{Ni}}}$ is generally larger than $\tilde D_{{\rm{MoMo}}}^{{\rm{Ni}}}$ . Moreover, $\tilde D_{{\rm{AlAl}}}^{{\rm{Ni}}}$ generally increases with concentration of Al, while $\tilde D_{{\rm{MoMo}}}^{{\rm{Ni}}}$ increases with concentrations of both Al and Mo. In contrast, the cross interdiffusivities can be either positive or negative. Average relative errors of $\tilde D_{{\rm{AlAl}}}^{{\rm{Ni}}}$ , $\tilde D_{{\rm{AlMo}}}^{{\rm{Ni}}}$ , $\tilde D_{{\rm{MoAl}}}^{{\rm{Ni}}}$ , and $\tilde D_{{\rm{MoMo}}}^{{\rm{Ni}}}$ were evaluated to be 2.4, 5.1, 16.1, and 1.7% using error propagation. Furthermore, our prediction of composition profiles and interdiffusion fluxes based on evaluated interdiffusivity matrices agrees quite well with measured data. Traditional Matano–Kirkaldy method was also applied to further verify the reliability of obtained interdiffusivities. Besides, three-dimensional planes of activation energies of main interdiffusivities were also evaluated using the Arrhenius equation.

Keywords

diffusionalloykinetics
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 11 , 14 June 2017 , pp. 2188 - 2201
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Jürgen Eckert

References

REFERENCES

Reed, R.C.: The Superalloys: Fundamentals and Applications (Cambridge University Press, Cambridge, U.K., 2006).Google Scholar
Pollock, T.M. and Tin, S.: Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure, and properties. J. Propul. Power 22, 361 (2006).Google Scholar
Divinski, S.V., Frank, St., Södervall, U., and Herzig, Chr.: Solute diffusion of Al-substituting elements in Ni3Al and the diffusion mechanism of the minority component. Acta Mater. 46, 4369 (1998).Google Scholar
Wei, H.X., Gong, W.Y., Huang, S., and Zhou, C.: Single-phase interdiffusion in the Ni3Al–Mo ternary system. Scr. Mater. 61, 53 (2011).Google Scholar
Henry, M.F.: Precipitation of γ′ in γ-α (Ni–Al–Mo) eutectics. Scr. Metall. 10, 955 (1976).Google Scholar
Nemoto, M., Honda, T., Nakagawa, Y.G., Saiga, Y., and Suto, H.: Microstructural studies of a Ni–Al–Mo directionally solidified eutectic composite. Trans. Jpn. Inst. Met. 21, 495 (1980).Google Scholar
Wakashima, K., Higuchi, K., Suzuki, T., and Umekawa, S.: Reinvestigation of phase equilibria in the system Ni–Al–Mo and its implication to the elevated temperature stability of γ/γ′-Mo aligned eutectics. Acta Metall. 31, 1937 (1983).Google Scholar
Wang, T., Sheng, G., Liu, Z.K., and Chen, L.Q.: Coarsening kinetics of γ′ precipitates in the Ni–Al–Mo system. Acta Mater. 56, 5544 (2008).Google Scholar
Wang, T.: An integrated approach for microstructure simulation: Application to nickel–aluminum–molybdenum alloys. Thesis (Ph.D.), The Pennsylvania State University, 2006.Google Scholar
Dayananda, M.A. and Kim, C.W.: Zero-flux planes and flux reversals in Cu–Ni–Zn diffusion couples. Metall. Trans. A 10, 1333 (1979).Google Scholar
Zhang, L., Du, Y., Ouyang, Y., Xu, H., Lu, X.G., Liu, Y., Kong, Y., and Wang, J.: Atomic mobilities, diffusivities and simulation of diffusion growth in the Co–Si system. Acta Mater. 56, 3940 (2008).Google Scholar
Sohn, Y.H. and Dayananda, M.A.: A double-serpentine diffusion path for a ternary diffusion couple. Acta Mater. 48, 1427 (2000).Google Scholar
Kirkaldy, J.S.: Diffusion in multicomponent metallic systems. Can. J. Phys. 35, 435 (1957).Google Scholar
Kirkaldy, J.S., Lane, J.E., and Mason, G.R.: Diffusion in multicomponent metallic systems: VII. Solutions of the multicomponent diffusion equations with variable coefficients. Can. J. Phys. 41, 2174 (1963).Google Scholar
Kirkaldy, J.S., Weichert, D., and Haq, Z-U.: Diffusion in multicomponent metallic systems. VI. Some thermodynamic properties of the D matrix and the corresponding solutions of the diffusion equations. Can. J. Phys. 41, 2166 (1963).Google Scholar
Kaufman, L. and Ågren, J.: CALPHAD, first and second generation-birth of the materials genome. Scr. Mater. 70, 3 (2014).Google Scholar
Olson, G.B. and Kuehmann, C.J.: Materials genomics: From CALPHAD to flight. Scr. Mater. 70, 25 (2014).Google Scholar
Chen, W., Zhang, L., Du, Y., Tang, C., and Huang, B.: A pragmatic method to determine the composition-dependent interdiffusivities in ternary systems by using a single diffusion couple. Scr. Mater. 90–91, 53 (2014).Google Scholar
Chen, W., Zhong, J., and Zhang, L.: An augmented numerical inverse method for determining the composition-dependent interdiffusivities in alloy systems by using a single diffusion couple. MRS Commun. 6, 295 (2016).Google Scholar
Lu, X.G., Cui, Y.W., and Jin, Z.P.: Experimental and thermodynamic investigation of the Ni–Al–Mo system. Metall. Mater. Trans. A 30, 1785 (1999).Google Scholar
Zhou, S.H., Wang, Y., Chen, L.Q., Liu, Z.K., and Napolitano, R.E.: Solution-based thermodynamic modeling of the Ni–Al–Mo system using first-principles calculations. Calphad 46, 124 (2014).Google Scholar
Manning, J.R.: Cross terms in the thermodynamic diffusion equations for multicomponent alloys. Metall. Trans. 1, 499 (1970).Google Scholar
Borgenstam, A., Engström, A., Höglund, L., and Ågren, J.: DICTRA, a tool for simulation of diffusional transformations in alloys. J. Phase Equilib. 21, 269 (2000).Google Scholar
Dayananda, M.A.: An analysis of concentration profiles for fluxes, diffusion depths, and zero-flux planes in multicomponent diffusion. Metall. Trans. A 14, 1851 (1983).Google Scholar
Whittle, D.P. and Green, A.: The measurement of diffusion coefficients in ternary systems. Scr. Mater. 8, 883 (1974).Google Scholar
Xu, H., Chen, W., Zhang, L., Du, Y., and Tang, C.: High-throughput determination of the composition-dependent interdiffusivities in Cu-rich fcc Cu–Ag–Sn alloys at 1073 K. J. Alloys Compd. 644, 687 (2015).Google Scholar
Chen, J., Xiao, J., Zhang, L., and Du, Y.: Interdiffusion in fcc Ni–X (X = Rh, Ta, W, Re and Ir) alloys. J. Alloys Compd. 657, 457 (2016).Google Scholar
Léchelle, J., Noyan, S., Aufore, L., Arredondo, A., and Audubert, E.: Volume interdiffusion coefficient and uncertainty assessment for polycrystalline materials. Diffus. Fundam. Org. 17, 1 (2012).Google Scholar
Zhang, L.J., Du, Y., Chen, Q., Steinbach, I., and Huang, B.Y.: Atomic mobilities and diffusivities in the fcc, L12 and B2 phases of the Ni–Al system. Int. J. Mater. Res. 101, 1461 (2010).Google Scholar
Liu, X.J., Hu, H.H., Han, J.J., Lu, Y., and Wang, C.P.: Assessment of the diffusional mobilities in fcc Ni–Nb and fcc Ni–Mo alloys. Calphad 38, 140 (2012).Google Scholar
Onsager, L.: Theories and problems of liquid diffusion. Ann. N. Y. Acad. Sci. 46, 241 (1945).Google Scholar
Liu, D.D., Zhang, L.J., Du, Y., Xu, H.H., and Jin, Z.P.: Ternary diffusion in Cu-rich fcc Cu–Al–Si alloys at 1073 K. J. Alloys Compd. 566, 156 (2013).Google Scholar
Laidler, K.J.: The development of the Arrhenius equation. J. Chem. Educ. 61, 494 (1984).Google Scholar