Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T01:01:06.077Z Has data issue: false hasContentIssue false
  • English
  • Français

High-rate dislocation motion in stable nanocrystalline metals

Published online by Cambridge University Press:  19 March 2019

Jeffrey T Lloyd
Jeffrey T Lloyd*
Affiliation:
Impact Physics Branch, US Army Research Laboratory, Aberdeen Proving Ground, Maryland 21005-5066, USA
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

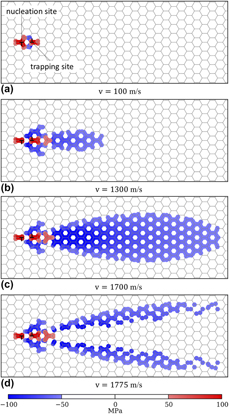
Dislocation-mediated plasticity in stable nanocrystalline metals, where grain boundary motion is suppressed, is revisited in the context of dislocation elastodynamics. The effect of transient waves that emanate from the generation and motion of dislocations is quantified for an idealized Cu–10 at.% Ta system with grain sizes on the order of 50 nanometers. Simulations indicate that for this material, as dislocation velocities approach 0.6–0.8 times the shear wave speed, grains several grain diameters away from the initial glide event experience a large transient shear stress for a finite duration. These transient shear stresses increase with increasing glide velocity and can activate nucleation sites far from the original nucleation event. These considerations are used to explain recent experimental observations of a lack of increase in flow stress with increasing loading rate, as well as localization resistance, in this class of stable nanocrystalline metals.

Keywords

dislocationsgrain boundariesstrength
Type
Invited Paper
Information
Journal of Materials Research , Volume 34 , Issue 13: Focus Issue: Intrinsic and Extrinsic Size Effects in Materials , 15 July 2019 , pp. 2252 - 2262
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Orowan, E.: Problems of plastic gliding. Proc. Phys. Soc. 52, 8 (1940).CrossRefGoogle Scholar
Conrad, H.: Grain size dependence of the plastic deformation kinetics in Cu. Mater. Sci. Eng., A 341, 216–228 (2003).CrossRefGoogle Scholar
Wei, Q., Cheng, S., Ramesh, K., and Ma, E.: Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume: Fcc versus bcc metals. Mater. Sci. Eng., A 381, 71–79 (2004).CrossRefGoogle Scholar
Argon, A. and Yip, S.: The strongest size. Philos. Mag. Lett. 86, 713–720 (2006).CrossRefGoogle Scholar
Dao, M., Lu, L., Asaro, R., De Hosson, J.T.M., and Ma, E.: Toward a quantitative understanding of mechanical behavior of nanocrystalline metals. Acta Mater. 55, 4041–4065 (2007).CrossRefGoogle Scholar
Wei, Y., Bower, A., and Gao, H.: Enhanced strain-rate sensitivity in fcc nanocrystals due to grain-boundary diffusion and sliding. Acta Mater. 56, 1741–1752 (2008).CrossRefGoogle Scholar
Zhang, K., Weertman, J., and Eastman, J.: Rapid stress-driven grain coarsening in nanocrystalline Cu at ambient and cryogenic temperatures. Appl. Phys. Lett. 87, 061921 (2005).CrossRefGoogle Scholar
Koch, C., Scattergood, R., Darling, K., and Semones, J.: Stabilization of nanocrystalline grain sizes by solute additions. J. Mater. Sci. 43, 7264–7272 (2008).CrossRefGoogle Scholar
Darling, K., Roberts, A.J., Mishin, Y., Mathaudhu, S.N., and Kecskes, L.J.: Grain size stabilization of nanocrystalline copper at high temperatures by alloying with tantalum. J. Alloys Compd. 573, 142–150 (2013).CrossRefGoogle Scholar
Darling, K., Huskins, E., Schuster, B., Wei, Q., and Kecskes, L.: Mechanical properties of a high strength Cu–Ta composite at elevated temperature. Mater. Sci. Eng., A 638, 322–328 (2015).CrossRefGoogle Scholar
Frolov, T., Darling, K., Kecskes, L., and Mishin, Y.: Stabilization and strengthening of nanocrystalline copper by alloying with tantalum. Acta Mater. 60, 2158–2168 (2012).CrossRefGoogle Scholar
Koju, R., Darling, K., Solanki, K., and Mishin, Y.: Atomistic modeling of capillary-driven grain boundary motion in Cu–Ta alloys. Acta Mater. 148, 311–319 (2018).CrossRefGoogle Scholar
Darling, K., Rajagopalan, M., Komarasamy, M., Bhatia, M., Hornbuckle, B., Mishra, R., and Solanki, K.: Extreme creep resistance in a microstructurally stable nanocrystalline alloy. Nature 537, 378 (2016).CrossRefGoogle Scholar
Regazzoni, G., Kocks, U., and Follansbee, P.: Dislocation kinetics at high strain rates. Acta Metall. 35, 2865–2875 (1987).CrossRefGoogle Scholar
Turnage, S., Rajagopalan, M., Darling, K., Garg, P., Kale, C., Bazehhour, B., Adlakha, I., Hornbuckle, B., Williams, C., Peralta, P., and Solanki, K.: Anomalous mechanical behavior of nanocrystalline binary alloys under extreme conditions. Nat. Commun. 9, 2699 (2018).CrossRefGoogle ScholarPubMed
Lin, I., Hirth, J., and Hart, E.: Plastic instability in uniaxial tension tests. Acta Metall. 29, 819–827 (1981).CrossRefGoogle Scholar
Wei, Q.: Strain rate effects in the ultrafine grain and nanocrystalline regimes influence on some constitutive responses. J. Mater. Sci. 42, 1709–1727 (2007).CrossRefGoogle Scholar
Darling, K., Tschopp, M., Guduru, R., Yin, W., Wei, Q., and Kecskes, L.: Microstructure and mechanical properties of bulk nanostructured Cu–Ta alloys consolidated by equal channel angular extrusion. Acta Mater. 76, 168–185 (2014).CrossRefGoogle Scholar
Bhatia, M., Rajagopalan, M., Darling, K., Tschopp, M., and Solanki, K.: The role of Ta on twinnability in nanocrystalline Cu–Ta alloys. Mater. Res. Lett. 5, 48–54 (2017).CrossRefGoogle Scholar
Clifton, R.: On the analysis of elastic/visco-plastic waves of finite uniaxial strain. In Shock Waves and the Mechanical Properties of Solids, Burke, J. and Weiss, V., eds. (Syracuse University Press, Syracuse, New York, 1971); pp. 73–116.Google Scholar
Kocks, U., Argon, A., and Ashby, M.: Thermodynamics and kinetics of slip. Prog. Mater. Sci. 19, 1–281 (1975).Google Scholar
Kuhlmann-Wilsdorf, D.: Theory of plastic deformation: Properties of low energy dislocation structures. Mater. Sci. Eng., A 113, 1–41 (1989).CrossRefGoogle Scholar
Taylor, J.: Dislocation dynamics and dynamic yielding. J. Appl. Phys. 36, 3146–3150 (1965).CrossRefGoogle Scholar
Johnston, W. and Gilman, J.: Dislocation multiplication in lithium fluoride crystals. J. Appl. Phys. 31, 632–643 (1960).CrossRefGoogle Scholar
Gupta, Y., Duvall, G., and Fowles, G.: Dislocation mechanisms for stress relaxation in shocked LiF. J. Appl. Phys. 46, 532–546 (1975).CrossRefGoogle Scholar
Roters, F., Raabe, D., and Gottstein, G.: Work hardening in heterogeneous alloys—A microstructural approach based on three internal state variables. Acta Mater. 48, 4181–4189 (2000).CrossRefGoogle Scholar
Johnston, W. and Gilman, J.: Dislocation velocities, dislocation densities, and plastic flow in lithium fluoride crystals. J. Appl. Phys. 30, 129–144 (1959).CrossRefGoogle Scholar
Yamakov, V., Wolf, D., Phillpot, S., Mukherjee, A., and Gleiter, H.: Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nat. Mater. 1, 45 (2002).CrossRefGoogle ScholarPubMed
Jones, O. and Mote, J.: Shock-induced dynamic yielding in copper single crystals. J. Appl. Phys. 40, 4920–4928 (1969).CrossRefGoogle Scholar
Johnson, J., Jones, O., and Michaels, T.: Dislocation dynamics and single crystal constitutive relations: Shock-wave propagation and precursor decay. J. Appl. Phys. 41, 2330–2339 (1970).CrossRefGoogle Scholar
Austin, R. and McDowell, D.: A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. Int. J. Plast. 27, 1–24 (2011).CrossRefGoogle Scholar
Lloyd, J., Clayton, J., Austin, R., and McDowell, D.: Plane wave simulation of elastic-viscoplastic single crystals. J. Mech. Phys. Solids 69, 14–32 (2014).CrossRefGoogle Scholar
Lloyd, J., Clayton, J., Becker, R., and McDowell, D.: Simulation of shock wave propagation in single crystal and polycrystalline aluminum. Int. J. Plast. 60, 118–144 (2014).CrossRefGoogle Scholar
Austin, R.: Elastic precursor wave decay in shock-compressed aluminum over a wide range of temperature. J. Appl. Phys. 123, 035103 (2018).CrossRefGoogle Scholar
Zhu, T., Li, J., Samanta, A., Leach, A., and Gall, L.: Temperature and strain-rate dependence of surface dislocation nucleation. Phys. Rev. Lett. 100, 025502 (2008).CrossRefGoogle ScholarPubMed
Van Swygenhoven, H., Derlet, P., and Froseth, A.: Nucleation and propagation of dislocations in nanocrystalline fcc metals. Acta Mater. 54, 1975–1983 (2006).CrossRefGoogle Scholar
Zhu, T., Li, J., Samanta, A., Kim, H., and Suresh, S.: Interfacial plasticity governs strain rate sensitivity and ductility in nanostructured metals. Proc. Natl. Acad. Sci. U. S. A. 104, 3031–3036 (2007).CrossRefGoogle ScholarPubMed
Zhu, T. and Li, J.: Ultra-strength materials. Prog. Mater. Sci. 55, 710–757 (2010).CrossRefGoogle Scholar
Lee, T., Robertson, I., and Birnbaum, H.: Prediction of slip transfer mechanisms across grain boundaries. Scr. Metall. 23, 799–803 (1989).CrossRefGoogle Scholar
Hunter, A., Leu, B., and Beyerlein, I.: A review of slip transfer: Applications of mesoscale techniques. J. Mater. Sci. 53, 5584–5603 (2018).CrossRefGoogle Scholar
Weertman, J.: High velocity dislocations. In Response of Metals to High Velocity Deformation. Metallurgical Society Conferences, Vol. 9, Shewmon, P. and Zackay, V., eds. (Interscience, New York, 1961); pp. 205–249.Google Scholar
Clifton, R. and Markenscoff, X.: Elastic precursor decay and radiation from nonuniformly moving dislocations. J. Mech. Phys. Solids 29, 227–251 (1981).CrossRefGoogle Scholar
Gurrutxaga-Lerma, B., Balint, D., Dini, D., and Sutton, A.: The mechanisms governing the activation of dislocation sources in aluminum at different strain rates. J. Mech. Phys. Solids 84, 273–292 (2015).CrossRefGoogle Scholar
Greenman, W., Vreeland, T. Jr., and Wood, D.: Dislocation mobility in copper. J. Appl. Phys. 38, 3595–3603 (1967).CrossRefGoogle Scholar
Chen, J., Tschopp, M., and Dongare, A.: Shock wave propagation and spall failure of nanocrystalline Cu/Ta alloys: Effect of Ta in solid-solution. J. Appl. Phys. 122, 225901 (2017).CrossRefGoogle Scholar
Joshi, S. and Ramesh, K.: Stability map for nanocrystalline and amorphous materials. Phys. Rev. Lett. 101, 025501 (2008).CrossRefGoogle ScholarPubMed
Guo, Y., Li, Y., Pan, Z., Zhou, F., and Wei, Q.: A numerical study of microstructure effect on adiabatic shear instability: Application to nanostructured/ultrafine grained materials. Mech. Mater. 42, 1020–1029 (2010).CrossRefGoogle Scholar
Eshelby, J.: Uniformly moving dislocations. Proc. Phys. Soc. 62, 307 (1949).CrossRefGoogle Scholar
Van der Giessen, E. and Needleman, A.: Discrete dislocation plasticity: A simple planar model. Modell. Simul. Mater. Sci. Eng. 3, 689 (1995).CrossRefGoogle Scholar
Gurrutxaga-Lerma, B., Balint, D., Dini, D., Eakins, D., and Sutton, A.: Dynamic discrete dislocation plasticity. In Advances in Applied Mechanics, Bordas, S., ed. Vol. 47 (Elsevier, London, U.K., 2014); ch. 2, pp. 93–224.Google Scholar
Markenscoff, X. and Clifton, R.: The nonuniformly moving edge dislocation. J. Mech. Phys. Solids 29, 253–262 (1981).CrossRefGoogle Scholar
Gurrutxaga-Lerma, B., Balint, D., Dini, D., Eakins, D., and Sutton, A.: A dynamic discrete dislocation plasticity method for the simulation of plastic relaxation under shock loading. Proc. R. Soc. A 469, 20130141 (2013).CrossRefGoogle Scholar
Darling, K., Kale, C., Turnage, S., Hornbuckle, B., Luckenbaugh, T., Grendahl, S., and Solanki, K.: Nanocrystalline material with anomalous modulus of resilience and springback effect. Scr. Mater. 141, 36–40 (2017).CrossRefGoogle Scholar