Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T16:36:53.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Graphene electronic structure in charge density waves

Published online by Cambridge University Press:  17 July 2017

John M. Vail ,
Oscar J. Hernandez ,
Mingsu Si  and
Zhoufei Wang
John M. Vail*
Affiliation:
Department of Physics and Astronomy and Winnipeg Institute for Theoretical Physics, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada
Oscar J. Hernandez
Affiliation:
Department of Physics and Astronomy, University of British Columbia, Vancouver, British Columbia V6T 1Z4, Canada; and TRIUMF, Vancouver, British Columbia V6T 2A3, Canada
Mingsu Si
Affiliation:
Key Laboratory for Magnetism and Magnetic Materials, Lanzhou University, Lanzhou 730000, People’s Republic of China
Zhoufei Wang
Affiliation:
Department of Physics, College of Science, South China Agricultural University, Guangzhou 510642, People’s Republic of China
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

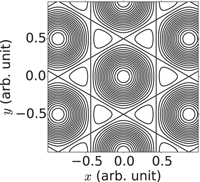
We introduce the idea that the electronic band structure of a charge density wave system may mimic that of graphene. In that case, a class of materials quite different from graphene might be opened up to exploit graphene’s remarkable properties. For such materials, their dynamical rather than static properties are crucial. The charge density wave system requires a wave geometry simply related to graphene and self-consistency among the electrons which requires the net Coulomb and phonon-mediated parts of the electron–electron interactions to be attractive. Our model leads to an analytical expression for the total energy in terms of the effective electron mass µ, the electron density ρ0, and the strength ${\tilde v_K}$ of the net electron–electron interaction. We examine the limitations set upon ${\tilde v_K}$ by self-consistency, stability, and the approximation in the electronic state calculation and find them to be mutually compatible.

Keywords

graphenecharge density waveselectronic structuremathematical modelstability
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 18 , 28 September 2017 , pp. 3494 - 3506
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Susan B. Sinnott

References

REFERENCES

Wallace, P.R.: The band theory of graphite. Phys. Rev. 71, 622 (1947).Google Scholar
Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., Grigorieva, I.V., and Firsov, A.A.: Electric field effect in atomically thin carbon films. Science 306, 666 (2004).Google Scholar
Fröhlich, H.: On the theory of superconductivity: The one-dimensional case. Proc. R. Soc. London, Ser. A 223, 296 (1954).Google Scholar
Cartlidge, E.: Graphene superconductivity seen. Phys. World 28(10), 6 (2015).Google Scholar
Rahnejat, K.G., Howard, A., Shuttleworth, N.E., Schofield, S.R., Iwaya, K., Hirijibehedin, C.F., Renner, C.H., Aeplli, G., and Ellerby, M.: Charge density waves in the graphene sheets of the superconductor CaC6 . Nat. Commun. 2, 558 (2011).Google Scholar
Ashcroft, N.W. and Mermin, N.D.: Solid State Physics (W. B. Saunders, Philadelphia, USA, 1976); ch. 10.Google Scholar