Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T17:57:34.907Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of the pore topology on the elastic modulus of organosilicate glasses

Published online by Cambridge University Press:  16 April 2013

Kong-Boon Yeap ,
Malgorzata Kopycinska-Mueller ,
Lei Chen ,
Yu Chen ,
Marco Jungmann ,
Reinhard Krause-Rehberg ,
Sukesh Mahajan ,
Joost Vlassak ,
Martin Gall  and
Ehrenfried Zschech
Kong-Boon Yeap
Affiliation:
Fraunhofer Institute for Nondestructive Testing, 01109 Dresden, Germany
Malgorzata Kopycinska-Mueller
Affiliation:
Fraunhofer Institute for Nondestructive Testing, 01109 Dresden, Germany; and Dresden University of Technology, Faculty of Electrical and Computer Engineering, 01068 Dresden, Germany
Lei Chen
Affiliation:
Queensland University of Technology, School of Chemistry, Physics and Mechanical Engineering department, Brisbane, Queensland 4001, Australia
Yu Chen
Affiliation:
National University of Singapore, Department of Mechanical Engineering, 117576 Singapore
Marco Jungmann
Affiliation:
Martin Luther University Halle, Department of Physics, 06120 Halle, Germany
Reinhard Krause-Rehberg
Affiliation:
Martin Luther University Halle, Department of Physics, 06120 Halle, Germany
Sukesh Mahajan
Affiliation:
SBA Materials, Inc., NE Albuquerque, New Mexico 87113
Joost Vlassak
Affiliation:
Harvard University, School of Engineering and Applied Sciences, Cambridge, Massachusetts 02138
Martin Gall
Affiliation:
Fraunhofer Institute for Nondestructive Testing, 01109 Dresden, Germany
Ehrenfried Zschech*
Affiliation:
Fraunhofer Institute for Nondestructive Testing, 01109 Dresden, Germany; and Dresden University of Technology, Faculty of Electrical and Computer Engineering, 01068 Dresden, Germany
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

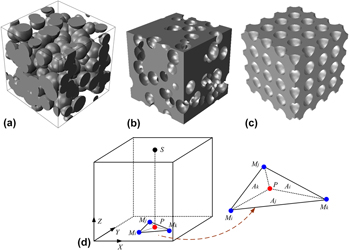
Optimization of the pore topology in organosilicate glass (OSG) is crucial in the development of dielectrics with an extremely low k-value and a relatively high Young’s modulus. In this paper, a finite-element modeling strategy is applied to develop a general understanding of the relationship between porosity, pore topology, and elastic modulus for the porous OSG thin films. This relationship in combination with the experimental elastic modulus data from nanoindentation (NI) studies is used to predict the pore structure of various OSG films. In addition, positron annihilation spectroscopy measurements are performed to determine the threshold porosity for the transition from nonoverlapping to overlapping porous structure. A similar threshold value is determined based on the finite-element modeling and experimental NI data.

Type
Articles
Information
Journal of Materials Research , Volume 28 , Issue 9 , 14 May 2013 , pp. 1262 - 1268
Copyright
Copyright © Materials Research Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Maex, K., Baklanov, M.R., Shamiryan, D., Iacopi, F., Brongersma, S.H., and Yanovitskaya, Z.S.: Low dielectric constant materials for microelectronics. J. Appl. Phys. 93(11), 8793 (2003).CrossRefGoogle Scholar
Dubois, G., Volksen, W., Magbitang, T., Miller, R.D., Gage, D.M., and Dauskardt, R.H.: Molecular network reinforcement of sol-gel glasses. Adv. Mater. 19(22), 3989 (2007).CrossRefGoogle Scholar
Gates, S.M., Dubois, G., Ryan, E.T., Grill, A., Liu, M., and Gidley, D.: Adjusting the skeleton and pore structure of porous SiCOH dielectrics. J. Electrochem. Soc. 156(10), G156 (2009).CrossRefGoogle Scholar
Jain, A., Rogojevic, S., Gill, W.N., Plawsky, J.L., Matthew, I., Tomozawa, M., and Simonyi, E.: Effects of processing history on the modulus of silica xerogel films. J. Appl. Phys. 90(11), 5832 (2001).CrossRefGoogle Scholar
Smirnov, E.A., Vanstreels, K., Verdonck, P., Ciofi, I., Shamiryan, D., Baklanov, M.R., and Phillips, M.: Evaluation of a new advanced low-k material. Jpn. J. Appl. Phys. 50(5), 05EB03 (2011).CrossRefGoogle Scholar
Zhao, D.Y., Feng, J.L., Huo, Q.S., Melosh, N., Fredrickson, G.H., Chmelka, B.F., and Stucky, G.D.: Triblock copolymer synthesis of mesoporous silica with periodic 50 to 300 angstrom pores. Science. 279(5350), 548 (1998).CrossRefGoogle Scholar
Wang, L.G., Ganor, M., Rokhlin, S.I., and Grill, A.: Nanoindentation analysis of mechanical properties of low to ultralow dielectric constant SiCOH films. J. Mater. Res. 20(8), 2080 (2005).CrossRefGoogle Scholar
Grill, A., Patel, V., Rodbell, K.P., Huang, E., Baklanov, M.R., Mogilnikov, K.P., Toney, M., and Kim, H.C.: Porosity in plasma enhanced chemical vapor deposited SiCOH dielectrics: A comparative study. J. Appl. Phys. 94(5), 3427 (2003).CrossRefGoogle Scholar
Yeap, K.B., Kopycinska-Muller, M., Hangen, U.D., Zambaldi, C., Hubner, R., Niese, S., and Zschech, E.: Nanometer deformation of elastically anisotropic materials studied by nanoindentation. Philos. Mag. 92(25–27), 3142 (2012).CrossRefGoogle Scholar
Schultz, P.J. and Lynn, K.G.: Interaction of positron beams with surfaces, thin films, and interfaces. Rev. Mod. Phys. 60(3), 701 (1988).CrossRefGoogle Scholar
ABAQUS User Manual, Version 6.9, SIMULIA (Simulia, Providence, RI, 2009).Google Scholar
Roberts, A.P. and Garboczi, E.J.: Elastic properties of model porous ceramics. J. Am. Ceram. Soc. 83(12), 3041 (2000).CrossRefGoogle Scholar
Roberts, A.P. and Garboczi, E.J.: Elastic properties of model random three-dimensional open-cell solids. J. Mech. Phys. Solids. 50(1), 33 (2002).CrossRefGoogle Scholar
Xia, Z.H., Zhang, Y.F., and Ellyin, F.: A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 40(8), 1907 (2003).CrossRefGoogle Scholar
Petkov, M.P., Wang, C.L., Weber, M.H., Lynn, K.G., and Rodbell, K.P.: Positron annihilation techniques suited for porosity characterization of thin films. J. Phys. Chem. B. 107(12), 2725 (2003).CrossRefGoogle Scholar
Garcia, A.A., Schut, H., Siebbeles, L.D.A., and van Veen, A.: Depth profiling of the degradation of OC1OC10-PPV monitored by positron beam analysis. Synthetic Met. 138(1–2), 43 (2003).CrossRefGoogle Scholar
Li, H., Lin, Y.B., Tsui, T.Y., and Vlassak, J.J.: The effect of porogen loading on the stiffness and fracture energy of brittle organosilicates. J Mater Res. 24(1), 107 (2009).CrossRefGoogle Scholar
Hashin, Z. and Shtrikman, S.: A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids. 11(2), 127 (1963).CrossRefGoogle Scholar