Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:54:43.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Dopant–dopant interactions in beryllium doped indium gallium arsenide: An ab initio study

Published online by Cambridge University Press:  14 January 2018

Vadym Kulish ,
Wenyuan Liu ,
Francis Benistant  and
Sergei Manzhos Open the ORCID record for Sergei Manzhos [Opens in a new window]
Vadym Kulish
Affiliation:
Department of Mechanical Engineering, National University of Singapore, Singapore 117576, Singapore
Wenyuan Liu
Affiliation:
Division of Physics and Applied Physics, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore 637371, Singapore
Francis Benistant
Affiliation:
GLOBALFOUNDRIES Singapore Pte Ltd., Singapore 738406, Singapore
Sergei Manzhos*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, Singapore 117576, Singapore
*
a) Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

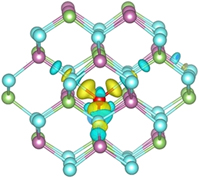
We present an ab initio study of dopant–dopant interactions in beryllium-doped InGaAs. We consider defect formation energies of various interstitial and substitutional defects and their combinations. We find that all substitutional–substitutional interactions could be neglected. On the other hand, interactions involving an interstitial defect are significant. Specially, interstitial Be is stabilized by about 0.9/1.0 eV in the presence of one/two BeGa substitutionals. Ga interstitial is also substantially stabilized by Be substitutionals. Two Be interstitials can form a metastable Be–Be–Ga complex with a dissociation energy of 0.26 eV/Be. Therefore, interstitial defects and defect–defect interactions should be considered in accurate models of Be-doped InGaAs. We suggest that In and Ga should be treated as separate atoms and not lumped into a single effective group III element, as has been done before. We identified dopant-centred states which indicate the presence of other charge states at finite temperatures, specifically, the presence of Beint +1 (as opposed to Beint +2 at 0 K).

Keywords

semiconductingdiffusionsimulation
Type
Invited Paper
Information
Journal of Materials Research , Volume 33 , Issue 4 , 28 February 2018 , pp. 401 - 413
Check for updates
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Susan B. Sinnott

References

REFERENCES

Del Alamo, J.A.: Nanometre-scale electronics with III–V compound semiconductors. Nature 479, 317 (2011).Google Scholar
Hu, J., Deal, M., and Plummer, J.: Modeling the diffusion of grown-in Be in molecular beam epitaxy GaAs. J. Appl. Phys. 78, 1595 (1995).Google Scholar
Koumetz, S., Marcon, J., Ketata, K., Ketata, M., Dubon-Chevallier, C., Launay, P., and Benchimol, J.: Be diffusion mechanisms in InGaAs during post-growth annealing. Appl. Phys. Lett. 67, 2161 (1995).Google Scholar
Marcon, J., Koumetz, S., Ketata, K., Ketata, M., and Caputo, J.: A comprehensive study of beryllium diffusion in InGaAs using different forms of kick-out mechanism. Eur. Phys. J.: Appl. Phys. 8, 7 (1999).Google Scholar
Endoh, A., Watanabe, I., and Mimura, T.: Monte Carlo simulation of InGaAs/strained-InAs/InGaAs channel HEMTs considering self-consistent analysis of 2-dimensional electron gas. In 24th International Conference on Indium Phosphide & Related Materials (IPRM), (IEEE, Santa Barbara, California 2012); p. 48.Google Scholar
Endoh, A., Watanabe, I., Kasamatsu, A., and Mimura, T.: Monte Carlo simulation of InAlAs/InGaAs HEMTs with various shape of buried gate. In Simulation of Semiconductor Processes and Devices (SISPAD), 2014 International Conference on (IEEE, 2014); p. 261.Google Scholar
Koumetz, S.D., Martin, P., and Murray, H.: A combined kick-out and dissociative diffusion mechanism of grown-in Be in InGaAs and InGaAsP. A new finite difference-Bairstow method for solution of the diffusion equations. J. Appl. Phys. 116, 103701 (2014).Google Scholar
Liu, W., Sk, M.A., Manzhos, S., Martin-Bragado, I., Benistant, F., and Cheong, S.A.: Grown-in beryllium diffusion in indium gallium arsenide: An ab initio, continuum theory and kinetic Monte Carlo study. Acta Mater. 125, 455 (2017).Google Scholar
Pinacho, R., Jaraiz, M., Castrillo, P., Martin-Bragado, I., Rubio, J., and Barbolla, J.: Modeling arsenic deactivation through arsenic-vacancy clusters using an atomistic kinetic Monte Carlo approach. Appl. Phys. Lett. 86, 252103 (2005).CrossRefGoogle Scholar
Legrain, F. and Manzhos, S.: Aluminum doping improves the energetics of lithium, sodium, and magnesium storage in silicon: A first-principles study. J. Power Sources 274, 65 (2015).CrossRefGoogle Scholar
Legrain, F. and Manzhos, S.: A first-principles comparative study of lithium, sodium, and magnesium storage in pure and gallium-doped germanium: Competition between interstitial and substitutional sites. J. Chem. Phys. 146, 034706 (2017).Google Scholar
Malyi, O.I., Tan, T.L., and Manzhos, S.: A comparative computational study of structures, diffusion, and dopant interactions between Li and Na insertion into Si. Appl. Phys. Express 6, 027301 (2013).Google Scholar
Malyi, O.I., Tan, T.L., and Manzhos, S.: In search of high performance anode materials for Mg batteries: Computational studies of Mg in Ge, Si, and Sn. J. Power Sources 233, 341 (2013).CrossRefGoogle Scholar
Malyi, O., Kulish, V.V., Tan, T.L., and Manzhos, S.: A computational study of the insertion of Li, Na, and Mg atoms into Si(111) nanosheets. Nano Energy 2, 1149 (2013).CrossRefGoogle Scholar
Legrain, F., Malyi, O.I., and Manzhos, S.: Comparative computational study of the diffusion of Li, Na, and Mg in silicon including the effect of vibrations. Solid State Ionics 253, 157 (2013).CrossRefGoogle Scholar
Oba, F., Togo, A., Tanaka, I., Paier, J., and Kresse, G.: Defect energetics in ZnO: A hybrid Hartree-Fock density functional study. Phys. Rev. B 77, 245202 (2008).Google Scholar
Freysoldt, C., Grabowski, B., Hickel, T., Neugebauer, J., Kresse, G., Janotti, A., and Van de Walle, C.G.: First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253 (2014).CrossRefGoogle Scholar
Chan, T.L. and Chelikowsky, J.R.: Controlling diffusion of lithium in silicon nanostructures. Nano Lett. 10, 821 (2010).Google Scholar
Peng, B., Cheng, F.Y., Tao, Z.L., and Chen, J.: Lithium transport at silicon thin film: Barrier for high-rate capability anode. J. Chem. Phys. 133, 034701 (2010).Google Scholar
Wan, W.H., Zhang, Q.F., Cui, Y., and Wang, E.G.: First principles study of lithium insertion in bulk silicon. J. Phys.: Condens. Matter 22, 415501 (2010).Google ScholarPubMed
Zhang, Q.F., Zhang, W.X., Wan, W.H., Cui, Y., and Wang, E.G.: Lithium insertion in silicon nanowires: An ab initio study. Nano Lett. 10, 3243 (2010).CrossRefGoogle ScholarPubMed
Zhang, Q.F., Cui, Y., and Wang, E.G.: Anisotropic lithium insertion behavior in silicon nanowires: Binding energy, diffusion barrier, and strain effect. J. Phys. Chem. C 115, 9376 (2011).Google Scholar
Tritsaris, G.A., Zhao, K.J., Okeke, O.U., and Kaxiras, E.: Diffusion of lithium in bulk amorphous silicon: A theoretical study. J. Phys. Chem. C 116, 22212 (2012).Google Scholar
Chou, C.Y. and Hwang, G.S.: Surface effects on the structure and lithium behavior in lithiated silicon: A first principles study. Surf. Sci. 612, 16 (2013).Google Scholar
Kim, H., Kweon, K.E., Chou, C.Y., Ekerdt, J.G., and Hwang, G.S.: On the nature and behavior of Li atoms in Si: A first principles study. J. Phys. Chem. C 114, 17942 (2010).Google Scholar
Kim, H., Chou, C.Y., Ekerdt, J.G., and Hwang, G.S.: Structure and properties of Li–Si alloys: A first-principles study. J. Phys. Chem. C 115, 2514 (2011).CrossRefGoogle Scholar
Kulish, V., Liu, W., and Manzhos, S.: A model for estimating chemical potentials in ternary semiconductor compounds: The case of InGaAs. MRS Adv. 2, 2909 (2017).Google Scholar
Varley, J.B., Janotti, A., and Van de Walle, C.G.: Group-V impurities in SnO2 from first-principles calculations. Phys. Rev. B 81, (2010).CrossRefGoogle Scholar
Janotti, A. and Van de Walle, C.G.: Native point defects in ZnO. Phys. Rev. B 76, 165202 (2007).Google Scholar
Komsa, H-P. and Pasquarello, A.: Comparison of vacancy and antisite defects in GaAs and InGaAs through hybrid functionals. J. Phys.: Condens. Matter 24, 045801 (2012).Google ScholarPubMed
Wang, J., Lukose, B., Thompson, M.O., and Clancy, P.: Ab initio modeling of vacancies, antisites, and Si dopants in ordered InGaAs. J. Appl. Phys. 121, 045106 (2017).Google Scholar
Kresse, G. and Joubert, D.: From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).Google Scholar
Lüder, J., Legrain, F., Chen, Y., and Manzhos, S.: Doping of active electrode materials for electrochemical batteries: An electronic structure perspective. MRS Commun. 7, 523 (2017).Google Scholar
Perdew, J.P., Burke, K., and Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).Google Scholar
Kresse, G. and Furthmüller, J.: Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).Google Scholar
Blochl, P.E.: Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).CrossRefGoogle ScholarPubMed
Monkhorst, H.J. and Pack, J.D.: Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).CrossRefGoogle Scholar
Murphy, S., Chroneos, A., Grimes, R., Jiang, C., and Schwingenschlögl, U.: Phase stability and the arsenic vacancy defect in In x Ga1−x As. Phys. Rev. B 84, 184108 (2011).CrossRefGoogle Scholar
Kratzer, P., Penev, E., and Scheffler, M.: Understanding the growth mechanisms of GaAs and InGaAs thin films by employing first-principles calculations. Appl. Surf. Sci. 216, 436 (2003).Google Scholar
Van de Walle, C.G. and Neugebauer, J.: First-principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 95, 3851 (2004).Google Scholar
Penrose, R.: A generalized inverse for matrices. Math. Proc. Cambridge Philos. Soc. 51, 406 (1955).Google Scholar
Gaskill, D., Bottka, N., Aina, L., and Mattingly, M.: Band-gap determination by photoreflectance of InGaAs and InAlAs lattice matched to InP. Appl. Phys. Lett. 56, 1269 (1990).Google Scholar
Perdew, J.P.: Density functional theory and the band gap problem. Int. J. Quantum Chem. 28, 497 (1985).Google Scholar
Mori-Sánchez, P., Cohen, A.J., and Yang, W.: Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 100, 146401 (2008).Google Scholar
Cohen, A.J., Mori-Sánchez, P., and Yang, W.: Insights into current limitations of density functional theory. Science 321, 792 (2008).Google Scholar
Burke, K.: Perspective on density functional theory. J. Chem. Phys. 136, 150901 (2012).Google Scholar
Cohen, A.J., Mori-Sánchez, P., and Yang, W.: Challenges for density functional theory. Chem. Rev. 112, 289 (2011).Google Scholar
Mirabella, S., De Salvador, D., Napolitani, E., Bruno, E., and Priolo, F.: Mechanisms of boron diffusion in silicon and germanium. J. Appl. Phys. 113, 3 (2013).Google Scholar