Article contents
Numerical modeling of centerline segregation by a combined 3-D and 2-D hybrid model during slab continuous casting
Published online by Cambridge University Press: 19 February 2018
Abstract
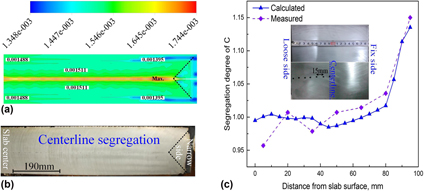
Centerline segregation is one of the typical internal defects, which occurs during slab continuous casting (CC). To investigate and predict the centerline segregation encountered in a continuously cast slab, a combined 3-D and 2-D hybrid simulation model for centerline segregation was developed. The average deviation between the calculated and experimented results reaches as low as 0.5%, which demonstrates that the hybrid simulation model has relatively high reliability. The centerline segregation of the slab was predicted accurately. The results show that macrosegregation occurring during the slab CC process has heredity. In the casting direction, the concentration of solutes in the liquid pool increases gradually until the casting has solidified completely. After complete solidification, the solutes’ concentration maintains an almost constant value. On the centerline, the maximum segregation degree occurs at a position roughly 614 mm from the slab center. The maximum centerline segregation degrees of C, Si, Mn, P, and S solutes are 1.163, 1.058, 1.045, 1.111, and 1.165, respectively.
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2018
Footnotes
Contributing Editor: Susan B. Sinnott
References
REFERENCES
- 5
- Cited by


