Article contents
Microstructure characterization and phase field analysis of dendritic crystal growth of γ-U and BCC-Mo dendrite in U–33 at.% Mo fast reactor fuel
Published online by Cambridge University Press: 09 November 2017
Abstract
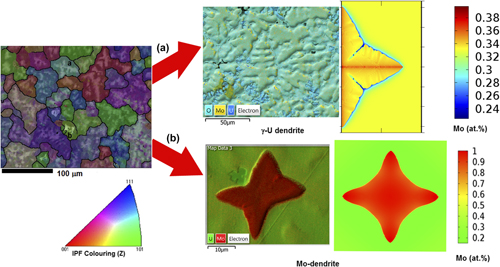
U–Mo metallic alloy is considered as an advanced fast reactor and research reactor fuel material. U–33 at.% Mo has a higher melting point than that of pure uranium metal. This provides a higher safety margin against fuel melting and diminishes fuel and clad interaction. The metallic fuels are fabricated through a melting-casting route, and the cast microstructure of U–33 at.% Mo has been characterized using optical microscope, scanning electron microscopy—energy dispersive spectroscopy, and Electron back scattered diffraction. These microstructures show dendrites of two different morphologies: (i) the γ-(U) dendrite with secondary branches and (ii) the equiaxed (Mo) dendrite without secondary branches and surrounded by a peritectic reaction product. In this article, for the first time, a phase field model has been developed for U–Mo alloys to understand the morphological evolution and the associated microsegregation of γ-(U) dendrites in the U–33 at.% Mo alloy. The evolution of the concentration and temperature field with the time and the effect of undercooling on the growth velocity of γ-(U) and (Mo) dendrites has been studied.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2017
Footnotes
Contributing Editor: Michele Manuel
References
REFERENCES
- 3
- Cited by



