Article contents
Linear free energy relationships in solid state diffusion processes
Published online by Cambridge University Press: 26 July 2012
Abstract
This paper presents a new form of linear free energy (LFE) relationship for diffusive mass transport in oxides and other binary compounds. The relationship applies to a family of related compounds. For a given substance, i, solid-state diffusivity is related to the equilibrium constant Ki or the free energy of transformation, 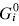 , via a transfer coefficient γ, through the expression ln Di = γ ln Ki + constant
, via a transfer coefficient γ, through the expression ln Di = γ ln Ki + constant 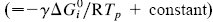 . The system investigated here is the series of suboxide intermediates of vanadium pentoxide formed during temperature-programmed synthesis of vanadium nitride. The value of γ for this series is 0.27. The diffusivity values are determined by fitting a mathematical model to the experimental data. Diffusivity data are presented graphically in contour diagrams which correlate pre-exponential values, activation energies, particle sizes, and heating rates used in the temperature-programmed syntheses. An Evans–Polanyi linear relation,
. The system investigated here is the series of suboxide intermediates of vanadium pentoxide formed during temperature-programmed synthesis of vanadium nitride. The value of γ for this series is 0.27. The diffusivity values are determined by fitting a mathematical model to the experimental data. Diffusivity data are presented graphically in contour diagrams which correlate pre-exponential values, activation energies, particle sizes, and heating rates used in the temperature-programmed syntheses. An Evans–Polanyi linear relation, 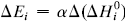 , relating activation energy, Ei, to enthalpy change of transformation,
, relating activation energy, Ei, to enthalpy change of transformation, 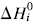 , via a transfer coefficient α = 0.53, is also shown to exist for the above system. The discrepancy between α and γ is resolved by using the Horiuti concept of the stoichiometric number of the rate-determining step.
, via a transfer coefficient α = 0.53, is also shown to exist for the above system. The discrepancy between α and γ is resolved by using the Horiuti concept of the stoichiometric number of the rate-determining step.
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 1997
References
REFERENCES
- 7
- Cited by


