Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binda, Federico
and
Krishna, Amalendu
2018.
Zero cycles with modulus and zero cycles on singular varieties.
Compositio Mathematica,
Vol. 154,
Issue. 1,
p.
120.
Krishna, Amalendu
2019.
Murthy’s conjecture on 0-cycles.
Inventiones mathematicae,
Vol. 217,
Issue. 2,
p.
549.
Gupta, Rahul
and
Krishna, Amalendu
2022.
Idele class groups with modulus.
Advances in Mathematics,
Vol. 404,
Issue. ,
p.
108376.


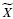 →
→ 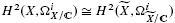 for
for 