Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T17:42:13.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Smoothness in Relative Geometry

Published online by Cambridge University Press:  15 November 2013

Florian Marty
Get access

Abstract

In [TVa], Bertrand Toën and Michel Vaquié defined a scheme theory for a closed monoidal category (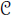 ⊗1). In this article, we define a notion of smoothness in this relative (and not necessarily additive) context which generalizes the notion of smoothness in the category of rings. This generalisation consists in replacing homological finiteness conditions by homotopical ones, using the Dold-Kan correspondence. To do this, we provide the category s 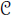of simplicial objects in a monoidal category 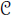and all the categories sA-mod, sA-alg (A ∈ sComm(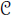)) with compatible model structures using the work of Rezk [R]. We then give a general notion of smoothness in sComm(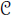). We prove that this notion is a generalisation of the notion of smooth morphism in the category of rings and is stable under composition and homotopy pushouts. Finally we provide some examples of smooth morphisms, in particular in ℕ-alg and Comm(Set).

Keywords

Symmetric monoidal categorysimplicial categorymodel categoryrelative geometrysmoothnesscohomology18D1019D2314F20
Type
Research Article
Information
Journal of K-Theory , Volume 12 , Issue 3 , December 2013 , pp. 461 - 491
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.Angeltveit, V., Enriched Reedy Categories, Proceedings of the American Mathematical Society 136(7) (2008), 2323–2332.Google Scholar
B.Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics 87, Springer-Verlag, New York-Berlin , 1982. x+308 pp.CrossRefGoogle Scholar
Bc.Borceux, F., Handbook ofCategorical Algebra II, Cambridge University Press, 1994, 443 pp.Google Scholar
EGAIV.Grothendieck, A., Eléments de géométrie algébrique IV, étude locale des schémas et des morphismes de schémas, partie IV, Inst. Hautes études sci. Publ. Math. 32 (1967), 361pp.Google Scholar
H.Hovey, M., Model Categories, Mathematical Surveys and Monographs 63, American Mathematical Society, Providence, RI, 1999. xii+209pp.Google Scholar
J.Jardine, J.F., Diagrams and Torsors, K-Theory 37(3) (2006), 291–309.Google Scholar
GJ.Goerss, P. and Jardine, J.F., Simplicial Homotopy Theory. Progr. Math. 174, Birkäuser Verlag, 1999.Google Scholar
M.Marty, F., Relative Zariski Open Objects. J. K-Theory 10 (2012), 9–39.CrossRefGoogle Scholar
M1.Marty, F., Des ouverts Zariski et des morphismes lisses en géométrie relative. Thése de doctorat. Available at http://thesesups.ups-tlse.fr/540/.Google Scholar
McL.Lane, S. Mac, Categories for the working mathematician, Graduate Text in Mathematics 5, Springer-Verlag, New York-Berlin, 1971. ix + 262pp.Google Scholar
Q.Quillen, D., On the (Co)-homology of Commutative Rings, Applications of categorical Algebra, Proc. ofthe Symposium in Pure Mathematics, 1968, New York - AMS, 1970.Google Scholar
R.Rezk, C., Every Homotopy Theory of Simplicial Algebras Admits a Proper Model, Topology Appl. 119 (2002), 65–94.Google Scholar
T1.Toën, B., Champs Affines - Selecta mathematica, New Series 12 (2006), 39–135.Google Scholar
TVa.Tbën, B. and Vaquié, M., Au-dessous de Spec (ℤ). J. K-Theory 3 (2009), 437–500.Google Scholar
TV.Toën, B., Vezzozi, G., Homotopical Algebraic Geometry II: Geometric Stacks and Applications, Memoirs of the American Mathematical Society 193 (2008), 230pp.CrossRefGoogle Scholar
V.Vezzani, A., Deitmar's versus Toën-Vaquié's schemes over , Mathematische Zeitschrift 271(3-4) (2012), 911–926.Google Scholar