Article contents
Perfect complexes on Deligne-Mumford stacks and applications
Published online by Cambridge University Press: 17 March 2009
Abstract
For a tame Deligne-Mumford stack X with the resolution property, we show that the Cartan-Eilenberg resolutions of unbounded complexes of quasicoherent sheaves are K-injective resolutions. This allows us to realize the derived category of quasi-coherent sheaves on X as a reflexive full subcategory of the derived category of 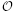 X-modules.
X-modules.
We then use the results of Neeman and recent results of Kresch to establish the localization theorem of Thomason-Trobaugh for the K-theory of perfect complexes on stacks of above type which have coarse moduli schemes. As a byproduct, we get a generalization of Krause's result about the stable derived categories of schemes to such stacks.
We prove Thomason's classification of thick triangulated tensor subcategories of D(perf / X). As the final application of our localization theorem, we show that the spectrum of D(perf / X) as defined by Balmer, is naturally isomorphic to the coarse moduli scheme of X, answering a question of Balmer for the tensor triangulated categories arising from Deligne-Mumford stacks.
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2009
References
- 10
- Cited by


