Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T12:00:16.136Z Has data issue: false hasContentIssue false
  • English
  • Français

Pairings in Hopf cyclic cohomology of algebras and coalgebras with coefficients

Published online by Cambridge University Press:  15 March 2010

I. Nikonov  and
G. Sharygin
I. Nikonov
Affiliation:
Dept. of Differential Geometry, Moscow State University, Leninskie Gory, Moscow, Russia, [email protected]
G. Sharygin
Affiliation:
ITEP, ul. B. Cheremushkinskaja, 25, Moscow, Russia, [email protected]
Get access

Abstract

This paper is concerned with the theory of cup products in the Hopf cyclic cohomology of algebras and coalgebras. We show that the cyclic cohomology of a coalgebra can be obtained from a construction involving the noncommutative Weil algebra. Then we introduce the notion of higher 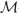-twisted traces and use a generalization of the Quillen and Crainic constructions (see [14] and [3]) to define the cup product. We discuss the relation of the cup product above and S-operations on cyclic cohomology. We show that the product we define can be realized as a combination of the composition product in bivariant cyclic cohomology and a map from the cyclic cohomology of coalgebras to bivariant cohomology. In the last section, we briefly discuss the relation of our constructions with that in [9]. More precisely, we propose still another construction of such pairings which can be regarded as an intermediate step between the “Crainic” pairing and that of [9]. We show that it coincides with what in [9] and as far its relation to Crainic's construction is concerned, we reduce the question to a discussuion of a certain map in cohomology (see the question at the end of section 5).

The results of the current paper were announced in [12].

Keywords

cyclic cohomology with coefficientsHopf algebras
Type
Research Article
Information
Journal of K-Theory , Volume 5 , Issue 2 , April 2010 , pp. 289 - 348
Copyright
Copyright © ISOPP 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Connes, A., Moscovici, H.: Cyclic cohomology and Hopf algebras, Lett. Math. Phys. 52, 97–108 (2000)CrossRefGoogle Scholar
2.Connes, A., Moscovici, H.: Hopf algebras, cyclic cohomology and the transverse index theorem, Commun. Math. Phys. 198, 199–246 (1998)CrossRefGoogle Scholar
3.Crainic, M.: Cyclic cohomology of Hopf algebras, J. Pure Appl. Algebra 166, 29–66 (2002)CrossRefGoogle Scholar
4.Cuntz, J., Quillen, D.: Algebra extensions and nonsingularity, J. Amer. Math. Soc. 8(2), 251–289 (1995)CrossRefGoogle Scholar
5.Cuntz, J., Quillen, D.: Cyclic homology and nonsingularity, J. Amer. Math. Soc. 8(2), 373–442 (1995)CrossRefGoogle Scholar
6.Goodwillie, T.G.: Cyclic homology, derivations, and the free loopspace, Topology 24(2), 187–215 (1985)CrossRefGoogle Scholar
7.Hajac, P.M., Khalkali, M., Rangipour, B., Sommerhäuser, M.: Hopf cyclic homology and cohomology with coefficients, C. R. Math. Acad. Sci. Paris 338(9), 667–672 (2004) (also available as preprint arXiv:math.KT/0306288 v.2)CrossRefGoogle Scholar
8.Karoubi, M.: Cohomologie cyclique et K-théorie, Astérisque 149 (1987)Google Scholar
9.Khalkhali, M., Rangipour, B.: Cup Products in Hopf cyclic Cohomology, C. R. Math. Acad. Sci. Paris 340, 9–14 (2005)CrossRefGoogle Scholar
10.Khalkhali, M., Rangipour, B.: A new cyclic module for Hopf algebras, K-theory 27, 111–131 (2002)CrossRefGoogle Scholar
11.Loday, J.L.: Cyclic homology, Springer-Verlag (1998)CrossRefGoogle Scholar
12.Nikonov, I., Sharygin, G.: On the Hopf-type cyclic cohomology with coefficients. In: C*- algebras and Elliptic Theory. Trends in Mathematics, pp.203–212. Birkhäuser Verlag, Basel, (2006)Google Scholar
13.Quillen, D.: Algebra cochains and cyclic cohomology, Publ. Math. IHES 68, 139–174 (1989)CrossRefGoogle Scholar
14.Quillen, D.: Chern-Simons forms and cyclic cohomology. In: The interface of Mathematics and particle Physics, 117–134, Oxford, 1988Google Scholar
15.Sharygin, G.: A new construction of characteristic classes for noncommutative algebraic principal bundles, Banach Center Publ. 61, 219–230 (2003)CrossRefGoogle Scholar
16.Taileffer, R.: Cyclic homology of Hopf algebras, K-Theory 24, 69–85 (2001)CrossRefGoogle Scholar