No CrossRef data available.
Published online by Cambridge University Press: 07 January 2008
Starting from the candidate Bloch-Beilinson filtration on 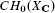 constructed in [L2], we develop and describe geometrically a series of Hodgetheoretic invariants Ψi defined on the graded pieces. Explicit formulas (in terms of currents and membrane integrals) are given for certain quotients of the Ψi, with applications to 0-cycles on products of curves.
constructed in [L2], we develop and describe geometrically a series of Hodgetheoretic invariants Ψi defined on the graded pieces. Explicit formulas (in terms of currents and membrane integrals) are given for certain quotients of the Ψi, with applications to 0-cycles on products of curves.