Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Blanc, David
Johnson, Mark W.
and
Turner, James M.
2010.
Higher homotopy operations and cohomology.
Journal of K-Theory,
Vol. 5,
Issue. 1,
p.
167.
Baues, Hans-Joachim
and
Blanc, David
2011.
Comparing cohomology obstructions.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 6,
p.
1420.
Blanc, David
Johnson, Mark W.
and
Turner, James M.
2012.
Higher homotopy operations and André–Quillen cohomology.
Advances in Mathematics,
Vol. 230,
Issue. 2,
p.
777.


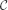 →
→ 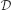 between model categories, we define a long exact sequence relating the homotopy groups of any
between model categories, we define a long exact sequence relating the homotopy groups of any 