Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T10:03:56.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Brauer group of a moduli space of parabolic vector bundles over a curve

Published online by Cambridge University Press:  18 February 2011

Indranil Biswas  and
Arijit Dey
Indranil Biswas
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005, India, [email protected]
Arijit Dey
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005, India, [email protected]
Get access

Abstract

Let 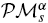be a moduli space of stable parabolic vector bundles of rank n ≥ 2 and fixed determinant of degree d over a compact connected Riemann surface X of genus g(X) ≥ g(X) = 2, then we assume that n > 2. Let m denote the greatest common divisor of d, n and the dimensions of all the successive quotients of the quasi–parabolic filtrations. We prove that the Brauer group Br 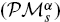is isomorphic to the cyclic group ℤ/mℤ. We also show that Br 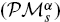is generated by the Brauer class of the Brauer–Severi variety over 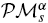obtained by restricting the universal projective bundle over X × .

Keywords

Brauer groupparabolic bundlemoduli space
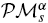Type
Research Article
Information
Journal of K-Theory , Volume 8 , Issue 3 , December 2011 , pp. 437 - 449
Copyright
Copyright © ISOPP 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Artin, M., Brauer–Severi varieties, (in: Brauer groups in ring theory and algebraic geometry), pp. 194–210, Lecture Notes in Math. 917, Springer, Berlin-New York, 1982.Google Scholar
2.Balaji, V., Biswas, I., Nagaraj, D. S. and Newstead, P. E., Universal families on moduli spaces of principal bundles on curves, Int. Math. Res. Not. (2006), Article Id 80641.CrossRefGoogle Scholar
3.Balaji, V., Biswas, I., Gabber, O. and Nagaraj, D. S., Brauer obstruction for a universal vector bundle, Comp. Rend. Math. Acad. Sci. Paris 345 (2007) 265–268.CrossRefGoogle Scholar
4.Bhosle, U. N., Picard group of the moduli spaces of vector bundles, Math. Ann. 314 (1999) 245–263.CrossRefGoogle Scholar
5.Boden, H. U. and Yokogawa, K., Rationality of moduli spaces of parabolic bundles, Jour. London Math. Soc. 59 (1999) 461–478.Google Scholar
6.Borel, A. and Remmert, R., Über kompakte homogene Kählersche Mannigfaltigkeiten, Math. Ann. 145 (1962) 429–439.CrossRefGoogle Scholar
7.Grothendieck, A., Le groupe de Brauer. I. Algébres d'Azumaya et interprétations diverses, (in: Dix Exposés sur la Cohomologie des Schémas), pp. 46–66, North-Holland, Amsterdam, 1968.Google Scholar
8.Grothendieck, A., Le groupe de Brauer. II. Théorie cohomologique, (in: Dix Exposés sur la Cohomologie des Schémas), pp. 67–87, North-Holland, Amsterdam, 1968.Google Scholar
9.Grothendieck, A., Le groupe de Brauer. III. Exemples et compléments, (in: Dix Exposés sur la Cohomologie des Schémas), pp. 88–188, North-Holland, Amsterdam, 1968.Google Scholar
10.Hoffmann, N., Rationality and Poincaré families for vector bundles with extra structure on a curve, Int. Math. Res. Not. 2007, doi:10.1093/imrn/rnm010.Google Scholar
11.Maruyama, M. and Yokogawa, K., Moduli of parabolic stable sheaves, Math. Ann. 293 (1992) 77–99.Google Scholar
12.Mehta, V. B. and Seshadri, C. S., Moduli of vector bundles on curves with parabolic structures, Math. Ann. 248 (1980) 205–239.Google Scholar
13.Milne, J. S., Étale Cohomology, Princeton University Press, Princeton, N.J., 1980.Google Scholar
14.Thaddeus, M., Geometric invariant theory and flips, Jour. Amer. Math. Soc. 9 (1996), 691–723.Google Scholar
15.Thaddeus, M., Variation of moduli of parabolic Higgs bundles, Jour. Reine Angew. Math. 547 (2002), 1–14.Google Scholar