Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bertapelle, A.
2014.
Generalized 1-motivic sheaves.
Journal of Algebra,
Vol. 420,
Issue. ,
p.
261.
Binda, Federico
Merici, Alberto
and
Saito, Shuji
2023.
Derived log Albanese sheaves.
Advances in Mathematics,
Vol. 417,
Issue. ,
p.
108936.


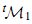 in [2] as well as the construction of the category of 1–motivic sheaves Shv
in [2] as well as the construction of the category of 1–motivic sheaves Shv