Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T06:31:59.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect complexes on Deligne-Mumford stacks and applications

Published online by Cambridge University Press:  17 March 2009

Amalendu Krishna
Amalendu Krishna
Affiliation:
[email protected] of MathematicsTata Institute Of Fundamental ResearchHomi Bhabha RoadMumbai,400005, India
Get access

Abstract

For a tame Deligne-Mumford stack X with the resolution property, we show that the Cartan-Eilenberg resolutions of unbounded complexes of quasicoherent sheaves are K-injective resolutions. This allows us to realize the derived category of quasi-coherent sheaves on X as a reflexive full subcategory of the derived category of 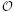X-modules.

We then use the results of Neeman and recent results of Kresch to establish the localization theorem of Thomason-Trobaugh for the K-theory of perfect complexes on stacks of above type which have coarse moduli schemes. As a byproduct, we get a generalization of Krause's result about the stable derived categories of schemes to such stacks.

We prove Thomason's classification of thick triangulated tensor subcategories of D(perf / X). As the final application of our localization theorem, we show that the spectrum of D(perf / X) as defined by Balmer, is naturally isomorphic to the coarse moduli scheme of X, answering a question of Balmer for the tensor triangulated categories arising from Deligne-Mumford stacks.

Keywords

Algebraic stacksAlgebraic K-theoryDerived category
Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 3 , December 2009 , pp. 559 - 603
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abramovich, D., Vistoli, A., Compactifying the space of stable maps, J. Amer. Math. Soc. 15 (1) (2001), 27-75CrossRefGoogle Scholar
2.Abramovich, D., Olsson, M., Vistoli, A., Tame stacks in positive characteristic, Preprint(2008), math.AG/0703310Google Scholar
3.Alper, J., Good moduli spaces for Artin stacks, Preprint, (2007), arXiv:0804.2242Google Scholar
4.Artin, M., Grothendieck Topologies, Harvard University Seminar, Spring, (1962)Google Scholar
5.Balmer, P., The spectrum of prime ideals in tensor triangulated categories, J. Reine Angew. Math. 588 (2005), 149-168CrossRefGoogle Scholar
6.Balmer, P., Presheaves of triangulated categories and reconstruction of schemes, Math. Ann. 324 (3) (2002), 557-580CrossRefGoogle Scholar
7.Bokstedt, M., Neeman, A., Homotopy limits in triangulated categories, Compositio Math. 86 (2) (1993), 209–234Google Scholar
8.Deligne, P., Mumford, D., The irreducibility of the space of curves of given genus, Inst. Hautes Etudes Sci. Publ. Math. 36 (1969), 75-109CrossRefGoogle Scholar
9.Edidin, D., Hasset, B., Kresch, A., Vistoli, A., Brauer groups and quotient stacks, Amer. J. Math. 123 (2001), 761-777CrossRefGoogle Scholar
10.Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics 52, Springer-Verlag, (1977)Google Scholar
11.Hartshorne, R., Residues and duality, Lecture Notes in Math. 20, Springer-Verlag, (1966)Google Scholar
12.Joshua, R., K -theory and absolute cohomology of algebraic stacks, Preprint (2005)Google Scholar
13.Joshua, R., Higher intersection theory on algebraic stacks. II, K-Theory 27 (3) (2002), 197-244CrossRefGoogle Scholar
14.Joshua, R., Bredon-style homology, cohomology and Riemann-Roch for algebraic stacks, Adv. Math. 209 (1) (2007), 1-68CrossRefGoogle Scholar
15.Keel, S., Mori, S., Quotients by groupoids, Ann. of Math. 145 (1) (1997), 193-213CrossRefGoogle Scholar
16.Keller, B., On the cyclic homology of ringed spaces and schemes, Doc. Math. 3 (1998), 231-259CrossRefGoogle Scholar
17.Knutson, D., Algebraic spaces, Lecture Notes in Mathematics 203, Springer-Verlag, Berlin, 1971Google Scholar
18.Kresch, A., On the geometry of Deligne-Mumford stacks, preprint (2006), to appear in Seattle ProceedingsGoogle Scholar
19.Kresch, A., Vistoli, A., On coverings of Deligne-Mumford stacks and surjectivity of the Brauer map, Bull. London Math. Soc. 36 (2) (2004), 188-192CrossRefGoogle Scholar
20.Krause, H., The stable derived category of a Noetherian scheme, Compos. Math. 141 (5) (2005), 1128-1162CrossRefGoogle Scholar
21.Laszlo, Y., Olsson, M., The six operations for sheaves on Artin stacks I: Finite Coefficients, Inst. Hautes Etudes Sci. Publ. Math. to appear (2008), also available at arXiv:math/0512097.CrossRefGoogle Scholar
22.Laumon, G., Moret-Baily, L., Champs algebriques, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 39, Springer-Verlag, Berlin, (2000)Google Scholar
23.MacLane, S., Categories for the working mathematician, Second edition, Graduate Texts in Mathematics 5, Springer-Verlag, (1998)Google Scholar
24.Milne, J., Ètale cohomology, Princeton University Press, Princeton, (1980)Google Scholar
25.Neeman, A., The connection between the K-Theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel, Ann. Sci. Ecole Norm. Sup. (4) 25 (5) (1992), 547-566CrossRefGoogle Scholar
26.Neeman, A., The Grothendieck duality theorem via Bousfield's techniques and Brown representability, J. Amer. Math. Soc. 9 (1) (1996), 205–236CrossRefGoogle Scholar
27.Neeman, A., A non-commutative generalisation of Thomason's localisation theorem. Non-commutative localization in algebra and topology, 60-80, London Math. Soc. Lecture Note Ser. 330, Cambridge Univ. Press, Cambridge, 2006Google Scholar
28.Neeman, A., Triangulated categories, Annals of Mathematics Studies 148, Princeton University Press, Princeton, NJ, 2001Google Scholar
29.Quillen, A., Higher algebraic K -theory - I, Lecture Notes in Math. 341, Springer-Verlag, New York, (1973) 85–147Google Scholar
30.Roos, J., Sur les foncteurs dérivés des produits infinis dans les catégories de Grothendieck, Examples et contre-examples, C. R. Acd. Sci. Paris Sér. A-B 263 (1966), A895–A898Google Scholar
31.Serpe, C., Resolution of unbounded complexes in Grothendieck categories, J. Pure Appl. Algebra 177 (1) (2003), 103-112CrossRefGoogle Scholar
32.Spaltenstein, N., Resolutions of unbounded complexes, Compositio Math. 65 (1988), 121-154Google Scholar
33.Thomason, R., Trobaugh, T., Higher algebraic K -theory of schemes and of derived categories, The Grothendieck Festschrift, Vol. III, 247–435, Progr. Math. 88, Birkhauser Boston, Boston, MA, 1990CrossRefGoogle Scholar
34.Thomason, R., Equivariant resolution, linearization, and Hilbert's fourteenth problem over arbitrary base schemes, Adv. in Math. 65 (1) (1987), 16–34CrossRefGoogle Scholar
35.Thomason, R., The classification of triangulated subcategories, Compositio Math. 105 (1) (1997), 1-27CrossRefGoogle Scholar
36.Toen, B., Théoreme de Riemann-Roch pour les champs de Deligne-Mumford, K-Theory 18 (1999), 33-76CrossRefGoogle Scholar
37.Totaro, B., The resolution property for schemes and stacks, J. Reine Angew. Math. 577 (2004), 1-22CrossRefGoogle Scholar
38.Viehweg, E., Quasi-projective moduli for polarized manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) 30, Springer-Verlag, (1995)Google Scholar
39.Vistoli, A., Intersection theory on algebraic stacks and on their moduli spaces, Invent. Math. 97 (1989), 613-670CrossRefGoogle Scholar
40.Weibel, C., Cyclic homology for schemes, Proc. Amer. Math. Soc. 124 (6) (1996), 1655-1662CrossRefGoogle Scholar
41.Weibel, C., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge University Press, Cambridge, (1994)Google Scholar