Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T08:48:51.781Z Has data issue: false hasContentIssue false
  • English
  • Français

On the motive of the group of units of a division algebra

Published online by Cambridge University Press:  17 March 2014

Evgeny Shinder
Evgeny Shinder*
Affiliation:
Edinburgh Hodge Institute, The University of Edinburgh, School of Mathematics, The King's Buildings, Edinburgh EH6 3JL, [email protected]
Get access

Abstract

We consider the algebraic group GL1 (A), where A is a division algebra of prime degree over a field F, and the associated motive in the Voevodsky category of motivic complexes 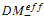(F). We relate the motive of GL1 (A) to the motive of the Čech simplicial scheme χ, associated to the Severi-Brauer variety of A, and compute the second differential in the resulting spectral sequence for motivic cohomology.

Keywords

division algebraSeveri-Brauer varietymotivic cohomology17A3511E5714F4219E15
Type
Research Article
Information
Journal of K-Theory , Volume 13 , Issue 3 , June 2014 , pp. 533 - 561
Copyright
Copyright © ISOPP 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

A.Artin, M., Brauer-Severi varieties. Brauer groups in ring theory and algebraic geometry (Wilrijk, 1981), pp. 194–210, Lecture Notes in Math. 917, Springer, Berlin-New York, 1982.Google Scholar
CGM.Chernousov, Vladimir; Gille, Stefan; Merkurjev, Alexander, Motivic decomposition of isotropic projective homogeneous varieties. Duke Math. J. 126(1) (2005), 137–159.CrossRefGoogle Scholar
BBD.Beilinson, A.A., Bernstein, J., Deligne, P., Faisceaux Pervers, Asterisque 100 (1982), Soc. Math. de France.Google Scholar
B.Biglari, S., Motives of reductive groups, Amer. J. Math. 134(1) (2012), 235–257.CrossRefGoogle Scholar
GG.Gillet, H.; Grayson, D., The loop space of the Q-construction. Illinois J. Math. 31(4) (1987), 574–597.CrossRefGoogle Scholar
GS.Gille, Philippe; Szamuely, Tams, Central simple algebras and Galois cohomology. Cambridge Studies in Advanced Mathematics 101, Cambridge University Press, Cambridge, 2006.Google Scholar
HK.Huber, Annette; Kahn, Bruno, The slice filtration and mixed Tate motives. Compos. Math. 142(4) (2006), 907–936.CrossRefGoogle Scholar
J.Jouanolou, J. P., Une suite exacte de Mayer-Vietoris en K-theorie algebrique. Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pp. 293–316. Lecture Notes in Math. 341, Springer, Berlin, 1973.Google Scholar
K.Karpenko, N.A., Grothendieck Chow motives of Severi-Brauer varieties. Algebra i Analiz 7(4) (1995), 196–213; translation in St. Petersburg Math. J. 7(4) (1996), 649–661.Google Scholar
Me.Merkurjev, A., Generic element in SK1 for simple algebras. K-Theory 7(1) (1993), 1–3.CrossRefGoogle Scholar
MS.Merkurjev, A., Suslin, A., Motivic cohomology of the simplicial motive of a Rost variety. J. Pure Appl. Algebra 214(11) (2010), 2017–2026.CrossRefGoogle Scholar
Mi.Milnor, J., Introduction to algebraic K-theory. Annals of Mathematics Studies 72. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1971.Google Scholar
MV.Morel, F., Voevodsky, V., 1-homotopy theory of schemes Inst. Hautes Études Sci. Publ. Math. 90 (1999), 45–143 (2001).CrossRefGoogle Scholar
Pu.Pushin, O., Higher Chern classes and Steenrod operations in motivic cohomology. K-Theory 31(4) (2004), 307–321.CrossRefGoogle Scholar
Q.Quillen, D., Higher algebraic K-theory. Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pp. 85–147. Lecture Notes in Math. 341, Springer, Berlin 1973.Google Scholar
R.Rost, M., The motive of a Pfister form. http://www.mathematik.uni-bielefeld.de/~rost/motive.htmlGoogle Scholar
Ri.Riou, J., Algebraic K-theory, 1-homotopy and Riemann-Roch theorems, J. Topol. 3(2) (2010), 229–264.CrossRefGoogle Scholar
S84.Suslin, A., Algebraic K-theory and the norm residue homomorphism, Current problems in mathematics 25, 115–207, Itogi Nauki i Tekhniki, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984Google Scholar
S91a.Suslin, A., K-theory and K-cohomology of certain group varieties. Algebraic K-theory, 53–74, Adv. Soviet Math. 4, Amer. Math. Soc., Providence, RI, 1991.Google Scholar
S91b.Suslin, A., SK1 of division algebras and Galois cohomology. Algebraic K-theory, 75–99, Adv. Soviet Math. 4, Amer. Math. Soc., Providence, RI, 1991.Google Scholar
S.Suslin, A., On the motive of a Severi-Brauer variety. Unpublished.Google Scholar
SV.Suslin, A., Voevdosky, V., Bloch-Kato conjecture and motivic cohomology with finite coefficients, The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 117–189, NATO Sci. Ser. C Math. Phys. Sci. 548, Kluwer Acad. Publ., Dordrecht, 2000.CrossRefGoogle Scholar
V98.Voevodsky, V., 1-homotopy theory., Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998). Doc. Math. 1998, Extra Vol. I, 579–604.Google Scholar
V00.Voevodsky, V., Triangulated categories of motives over a field. Cycles, transfers, and motivic homology theories, 188–238, Ann. of Math. Stud. 143, Princeton Univ. Press, Princeton, NJ, 2000.Google Scholar
V03a.Voevodsky, V., Motivic cohomology with Z/2-coefficients. Publ. Math. Inst. Hautes Études Sci. 98 (2003), 59–104.CrossRefGoogle Scholar
V03b.Voevodsky, V., Motivic cohomology groups are isomorphic to Chow groups in any characteristic., IMRN (2002), 351–355.Google Scholar
V10a.Voevodsky, V., Motives over simplicial schemes. J. K-Theory 5(1) (2010), 1–38.CrossRefGoogle Scholar
V10b.Voevodsky, V., Cancellation Theorem, Documenta Math. Extra Volume: Andrei A. Suslin's Sixtieth Birthday (2010), 671–685.Google Scholar