Article contents
Modular Invariants and Twisted Equivariant K-theory II: Dynkin diagram symmetries
Published online by Cambridge University Press: 26 June 2013
Abstract
The most basic structure of chiral conformal field theory (CFT) is the Verlinde ring. Freed-Hopkins-Teleman have expressed the Verlinde ring for the CFT's associated to loop groups, as twisted equivariant K-theory. We build on their work to express K-theoretically the structures of full CFT. In particular, the modular invariant partition functions (which essentially parametrise the possible full CFTs) have a rich interpretation within von Neumann algebras (subfactors), which has led to the developments of structures of full CFT such as the full system (fusion ring of defect lines), nimrep (cylindrical partition function), alpha-induction etc. Modular categorical interpretations for these have followed. For the generic families of modular invariants (i.e. those associated to Dynkin diagram symmetries), we provide a K-theoretic framework for these other CFT structures, and show how they relate to D-brane charges and charge-groups. We also study conformal embeddings and the 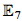 modular invariant of SU(2), as well as some families of finite group doubles. This new K-theoretic framework allows us to simplify and extend the less transparent, more ad hoc descriptions of these structures obtained previously within CFT.
modular invariant of SU(2), as well as some families of finite group doubles. This new K-theoretic framework allows us to simplify and extend the less transparent, more ad hoc descriptions of these structures obtained previously within CFT.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2013
References
- 8
- Cited by


