Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T16:35:21.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy classification and the generalized Swan homomorphism

Published online by Cambridge University Press:  07 January 2009

F.E.A. Johnson
F.E.A. Johnson
Affiliation:
[email protected] of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K.
Get access

Abstract

In his fundamental paper on group cohomology [20] R.G. Swan defined a homomorphism 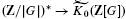for any finite group G which, in this restricted context, has since been used extensively both in the classification of projective modules and the algebraic homotopy theory of finite complexes ([3], [18], [21]). We extend the definition so that, for suitable modules J over reasonably general rings Λ, it takes the form 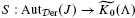here 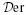is the quotient of the category of Λ-homomorphisms obtained by setting ‘projective = 0’. We then employ it to give an exact classification of homotopy classes of extensions 0 → J → Fn → … → F0 → F0 → M → 0 where each Fr is finitely generated free.

Keywords

Derived module categorycoprojective moduleSwan homomorphismalgebraic n-complex
Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 3 , December 2009 , pp. 491 - 536
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Auslander, M. and Bridger, M. ; Stable module theory. Memoirs of the AMS 94, 1969CrossRefGoogle Scholar
2.Auslander, M., Reiten, I. and Smalo, S. ; Representation theory of Artin algebras. Cambridge University Press, 1995Google Scholar
3.Bentzen, S. and Madsen, I. ; On the Swan subgroup of certain periodic groups: Math. Ann. 264 (1983), 447–474Google Scholar
4.Bieri, R. and Eckmann, B. ; Groups with homological duality generalizing Poincaré Duality: Invent. Math. 20 (1973), 103–124CrossRefGoogle Scholar
5.Browning, W. ; Homotopy types of certain finite C.W. complexes with finite fundamental group. Ph.D Thesis, Cornell University, 1978Google Scholar
6.Browning, W. ; Truncated projective resolutions over a finite group. (unpublished notes) ETH, 04 1979Google Scholar
7.Cohn, P.M. ; Some remarks on the invariant basis property: Topology 5 (1966), 215–228Google Scholar
8.Cohn, P.M. ; Skew fields. Cambridge University Press, 1995CrossRefGoogle Scholar
9.Cockroft, W.H. and Swan, R.G. ; On the homotopy types of certain two-dimensional complexes: Proc. L. M. S. 11 (3) (1961), 194–202Google Scholar
10.Dyer, M.N. and Sieradski, A.J. ; Trees of homotopy types of two-dimensional CW complexes: Comment. Math. Helv. 48 (1973), 31–44Google Scholar
11.Edwards, T.M.. Algebraic 2-complexes over low dimensional infinite abelian groups. PhD Thesis, University College London, 2006Google Scholar
12.Hilton, P.J.. Homotopy theory and duality. Notes on Mathematics and its applications, Gordon and Breach, 1965Google Scholar
13.Johnson, F.E.A. ; Stable modules and the D(2)-problem. LMS Lecture Notes In Mathematics 301, Cambridge University Press, 2003Google Scholar
14.Johnson, F.E.A. ; Rigidity of hyperstable complexes: Archiv der Math. 90 (2008), 123–132Google Scholar
15.Johnson, F.E.A. and Wall, C.T.C. ; On groups satisfying Poincaré Duality: Ann. of Math. 96 (1972), 592–598CrossRefGoogle Scholar
16.MacLane, S. ; Homology. Springer-Verlag, 1963Google Scholar
17.Magurn, B. ; An algebraic introduction to K-theory. Cambridge University Press, 2002CrossRefGoogle Scholar
18.Milgram, R.J. ; Odd index subgroups of units in cyclotomic fields and applications: published in Lecture Notes in Mathematics 854, 269–298, Springer-Verlag, 1981Google Scholar
19.Northcott, D.G. ; Finite free resolutions. Cambridge University Press, 1964Google Scholar
20.Swan, R.G. ; Periodic resolutions for finite groups: Ann. of Math. 72 (1960), 267–291Google Scholar
21.Swan, R.G. ; Projective modules over binary polyhedral groups: Journal für die Reine und Angewandte Math. 342 (1983), 66–172Google Scholar
22.Wall, C.T.C. ; Finiteness conditions for CW complexes II: Proc. Roy. Soc. A 295 (1966), 129–139Google Scholar
23.Weyman, J. ; Cohomology of vector bundles and syzygies. Cambridge University Press, 2003CrossRefGoogle Scholar
24.Yoneda, N. ; On the homology theory of modules: J. Fac. Sci. Tokyo, Sec. I, 7 (1954), 193–227Google Scholar