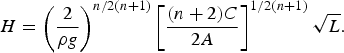1. INTRODUCTION
A volume/area scaling relation for glaciers and ice caps is widely used to estimate the volume of glaciers and the loss of ice in relation with global climate change and sea-level rise (e.g., Raper and Braithwaite, Reference Raper and Braithwaite2006; Meier and others, Reference Meier2007; Bahr and others, Reference Bahr, Dyurgerov and Meier2009; Leclercq and others, Reference Leclercq, Oerlemans and Gogley2011; Radić and Hock, Reference Radić and Hock2011; Mernild and others, Reference Mernild, Lipscomb, Bahr, Radić and Zemp2013). Other scaling relations (e.g. basal stress/area or response timescaling are used successfully in glaciology (e.g. Jóhannesson and others, Reference Jóhannesson, Raymond and Waddington1989; Pfeffer and others, Reference Pfeffer, Sassolas, Bahr and Meier1998; Harrison and others, Reference Harrison, Elsberg and Echelmeyer2001, Reference Harrison, Raymond and Echelmeyer2003; Lüthi, Reference Lüthi2009; Raper and Braithwaite, Reference Raper and Braithwaite2009; Clarke and others, Reference Clarke2013). A volume/area scaling of the form
where V and S are the volume and surface area of glaciers or ice caps (km3 and km2, respectively), has been shown to fit empirical data. From the theoretical point of view, this relation Eqn (1) is derived using scaling analysis (Bahr and others, Reference Bahr, Meier and Peckam1997, Reference Bahr, Pfeffer and Kaser2015) according to the Buckingham Pi theorem (Buckingham, Reference Buckingham1914). Note the recent review (Bahr and others, Reference Bahr, Pfeffer and Kaser2015), which dispels common misconceptions, and references therein for a detailed exposition. While it is easy to determine the area S using, for example, aerial surveys, it is much more difficult to assess directly the volume, V of the ice. The exponent γ in Eqn (1) is believed to be a universal constant, as is theoretically sound in scaling analysis, while the value of c is characteristic of the specific glacier or ice cap considered (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). Different values of γ are predicted for ice caps and for valley glaciers, but the exponent is believed to be universal within each of these two classes (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). It is conceivable, at least in principle, that more than two classes exist, and other authors report a range of values for different types of glaciers (Adhikari and Marshall, Reference Adhikari and Marshall2012). However, the transition from one value of γ to another appears to be abrupt, not gradual, as described by percolation theory (Bahr and Pfeffer, Reference Bahr and Pfeffer2016).
The law Eqn (1) is used in a statistical sense and it can also be used for individual glaciers and ice caps if one contents oneself with obtaining an order of magnitude estimate for the volume V.
The universal exponent γ is predicted using scaling analysis and assuming certain closure relations that determine how various quantities scale with length (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). Fundamental quantities involved in the scaling relations for glaciers and ice caps are the glacier longitudinal dimension l, width w and thickness h. For valley glaciers (but not for ice sheets and ice caps), a shape factor F is also introduced, which describes how the valley walls partially support the ice (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010). While the shape factor is not necessary in every derivation of the volume/area scaling law (in fact it is used only in one of the three derivations of Bahr and others (Bahr and others, Reference Bahr, Pfeffer and Kaser2015), it is assumed (Bahr and others, Reference Bahr, Meier and Peckam1997) that S ~ [l][w] and
with
where, a posteriori, f = 0 is found to be appropriate (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). A further assumption used in scaling analysis is that the mass-balance rate
![]() $\dot b$
of the ice is described by a power law,
$\dot b$
of the ice is described by a power law,
Numerous authors have analyzed empirical data for glaciers and ice caps determining values for the parameters q, m and γ (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). Scaling analysis does not need to assume a priori a scaling relation h ~ [l]s. However, it is clear that the extension in the third-spatial dimension is relevant for the volume of the ice and the volume/area relation Eqn (1) clearly has implications for theoretical models of the local ice thickness h(x) (where x is a longitudinal coordinate along the ice bed). Longitudinal glacier profiles have been the domain of a separate body of literature aiming at solving analytically ordinary differential equations derived from specific assumptions on the physical behaviour of ice under stress, which a priori has nothing to do with the theory of scaling. It is, however, interesting to relate these two separate areas of glaciology.
We examine the implications of the empirical values of the exponent γ and of the parameters (q, m, n) for analytical theoretical solutions of the differential equations that model the longitudinal profile h(x) of the ice. These theoretical models are based on assumptions about the microphysics of ice (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010). The simplest assumption used in the early days of theoretical modeling is that of perfectly plastic ice (Nye, Reference Nye1952), which is however unrealistic. A better model to describe the microscopic behaviour of ice is Glen's law (Glen, Reference Glen1955), which relates the strain rates
![]() $\dot \varepsilon _{ij}$
and the deviatoric stresses s
ij
in the ice,
$\dot \varepsilon _{ij}$
and the deviatoric stresses s
ij
in the ice,
where
![]() ${\rm {\cal A}}$
is a (temperature-dependent) constant, σ
eff is the effective stress, and n = 3 for ice flow, while n → ∞ for perfectly plastic ice (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010). A few analytical solutions h(x) are known for the differential equations modeling the local ice thickness (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010) and power-law relations h ~ [l]
s
emerge from these solutions, although they are not usually noted in the literature. These relations are compared below with the empirical values of the exponent γ and the parameters (q,m,n) relevant for the scaling analyses leading to Eqn (1).
${\rm {\cal A}}$
is a (temperature-dependent) constant, σ
eff is the effective stress, and n = 3 for ice flow, while n → ∞ for perfectly plastic ice (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010). A few analytical solutions h(x) are known for the differential equations modeling the local ice thickness (Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010) and power-law relations h ~ [l]
s
emerge from these solutions, although they are not usually noted in the literature. These relations are compared below with the empirical values of the exponent γ and the parameters (q,m,n) relevant for the scaling analyses leading to Eqn (1).
2. USING DATA ON VOLUME/AREA SCALING TO TEST LONGITUDINAL PROFILE MODELS
Let us consider now how the characteristic thickness h of a glacier or ice cap scales with length, h ~ [l] s . Since the ice volume is V ~ [l][w][h] and S ~ [l][w], a scaling relation Eqn (1) is related to the scaling of the thickness. Theoretical models of longitudinal glacier profiles h(x) solve nonlinear ordinary differential equations and make precise predictions for the value of the scaling exponent s, which can be compared with the result of scaling analysis and with data.
The scaling h ~ [l] s with exponent
is predicted for ice caps by Bahr and others (Reference Bahr, Pfeffer and Kaser2015). Since V ~ [l][w][h] ~ l
q+s+1 and S ~ [l][w] ~ [l]
q+1, it is
![]() $V \sim S^{\textstyle{{q + s + 1} \over {q + 1}}}$
or
$V \sim S^{\textstyle{{q + s + 1} \over {q + 1}}}$
or
for ice caps (Eqn (132) of Bahr and others, Reference Bahr, Pfeffer and Kaser2015). For glaciers, instead, it is predicted that
and (Eqn (122) of Bahr and others, Reference Bahr, Pfeffer and Kaser2015)
2.1. Ice caps
For ice caps, it is believed that m ≃ 0, corresponding to a mass-balance rate independent of the length. For a horizontal bed and thick ice, as is commonly assumed for ice caps (Paterson, Reference Paterson1994; Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010), an order of magnitude estimate provides h ~ [l]1/2 (Faraoni and Vokey, Reference Faraoni and Vokey2015). This argument assumes a surface slope θ ~ h/l, which is typical of ice caps and large glaciers. Setting m = 0 in Eqn (8) gives s = 1/2 and then γ = 1 + (1/2(q + 1)) irrespective of the value of n (although n = 3 is certainly the appropriate value for ice flow). Because of the approximate cylindrical symmetry of ice caps burying the underlying topography, S ~ [w][l] ~ [l] q+1 ~ πl 2 and q = 1, giving γ = 5/4 = 1.25, which matches the data (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). Since, for the appropriate value m = 0 of the mass-balance rate parameter it can only be s = 1/2, theoretical models for longitudinal ice-cap profiles h(x) do not have wiggle room. Let us review them.
-
• Nye's parabolic profile: for perfectly plastic ice is (Nye, Reference Nye1951a, Reference Nyeb; Cuffey and Paterson, Reference Cuffey and Paterson2010)
 $$H = \sqrt {\displaystyle{{2\tau _{\rm b}} \over {\rho g}}} \sqrt L, $$
$$H = \sqrt {\displaystyle{{2\tau _{\rm b}} \over {\rho g}}} \sqrt L, $$
where τ b is the basal stress. The maximum ice thickness H corresponds to x = 0 and the glacier terminus is located at x = L. Clearly, this model fits the data but the assumption of perfectly plastic ice is unphysical (Paterson, Reference Paterson1994; Hooke, Reference Hooke2005; Cuffey and Paterson, Reference Cuffey and Paterson2010).
-
• Vialov profile: The Vialov longitudinal profile for ice satisfying Glen's law (Vialov, Reference Vialov1958; Paterson, Reference Paterson1994; Hooke, Reference Hooke2005; Greve and Blatter, Reference Greve and Blatter2009; Cuffey and Paterson, Reference Cuffey and Paterson2010) is
(14) $$h(x) = H\left[ {1 - {\left( {\displaystyle{x \over L}} \right)}^{n + 1/n}} \right]^{n/2(n + 1)},$$
(15)
$$h(x) = H\left[ {1 - {\left( {\displaystyle{x \over L}} \right)}^{n + 1/n}} \right]^{n/2(n + 1)},$$
(15) $$H = \left( {\displaystyle{2 \over {\rho g}}} \right)^{n/2(n + 1)}\left[ {\displaystyle{{(n + 2)C} \over {2A}}} \right]^{1/2(n + 1)}\sqrt L. $$
$$H = \left( {\displaystyle{2 \over {\rho g}}} \right)^{n/2(n + 1)}\left[ {\displaystyle{{(n + 2)C} \over {2A}}} \right]^{1/2(n + 1)}\sqrt L. $$
It is a solution of the nonlinear Vialov differential equation for the longitudinal profile h(x) (Vialov, Reference Vialov1958) when
![]() $\dot b$
= const. (corresponding to m = 0). Also for the Vialov exact profile, the maximum thickness H scales with
$\dot b$
= const. (corresponding to m = 0). Also for the Vialov exact profile, the maximum thickness H scales with
![]() $\sqrt L $
.
$\sqrt L $
.
-
• New power-law solutions of the Vialov equation: A new analytical formal solution of the Vialov differential equation for longitudinal glacier profiles corresponding to mass-balance rate
 $\dot b = c_mx^m$
is the power-law profile (Faraoni and Vokey, Reference Faraoni and Vokey2016),
(16)
$\dot b = c_mx^m$
is the power-law profile (Faraoni and Vokey, Reference Faraoni and Vokey2016),
(16) $$h(x) = H\left( {\displaystyle{x \over L}} \right)^s,\quad s = \displaystyle{{n + m + 1} \over {2(n + 1)}},$$
(17)
$$h(x) = H\left( {\displaystyle{x \over L}} \right)^s,\quad s = \displaystyle{{n + m + 1} \over {2(n + 1)}},$$
(17) $$H = \left[ {\left( {\displaystyle{{n + 2} \over {2A}}} \right) \displaystyle{{c_mL^{n + m + 1}} \over {{\left( {\beta \rho g} \right)}^n}}} \right]^{1/2(n + 1)} \equiv h_0L^s, $$
$$H = \left[ {\left( {\displaystyle{{n + 2} \over {2A}}} \right) \displaystyle{{c_mL^{n + m + 1}} \over {{\left( {\beta \rho g} \right)}^n}}} \right]^{1/2(n + 1)} \equiv h_0L^s, $$
where now, x = 0 is the glacier terminus and the maximum thickness H of the ice is attained at x = L. The value Eqn (16) of s reproduces exactly, for all values of the parameters (n,m,q), that of Eqn (8) first predicted by Bahr and others (Reference Bahr, Pfeffer and Kaser2015) by scaling analysis.
For
![]() $\dot b = {\rm const}. \equiv c_0$
(corresponding to m = 0) one obtains (Faraoni and Vokey, Reference Faraoni and Vokey2016)
$\dot b = {\rm const}. \equiv c_0$
(corresponding to m = 0) one obtains (Faraoni and Vokey, Reference Faraoni and Vokey2016)
 $$H = \left( {\displaystyle{2 \over {\rho g}}} \right)^{n/2(n + 1)}\left[ {\displaystyle{{(n + 2)c_0} \over {2A}}} \right]^{1/2(n + 1)}\sqrt L \equiv h_0\sqrt L. $$
$$H = \left( {\displaystyle{2 \over {\rho g}}} \right)^{n/2(n + 1)}\left[ {\displaystyle{{(n + 2)c_0} \over {2A}}} \right]^{1/2(n + 1)}\sqrt L \equiv h_0\sqrt L. $$
Apart from the value of the constant H (which is, however, still proportional to
![]() $\sqrt L $
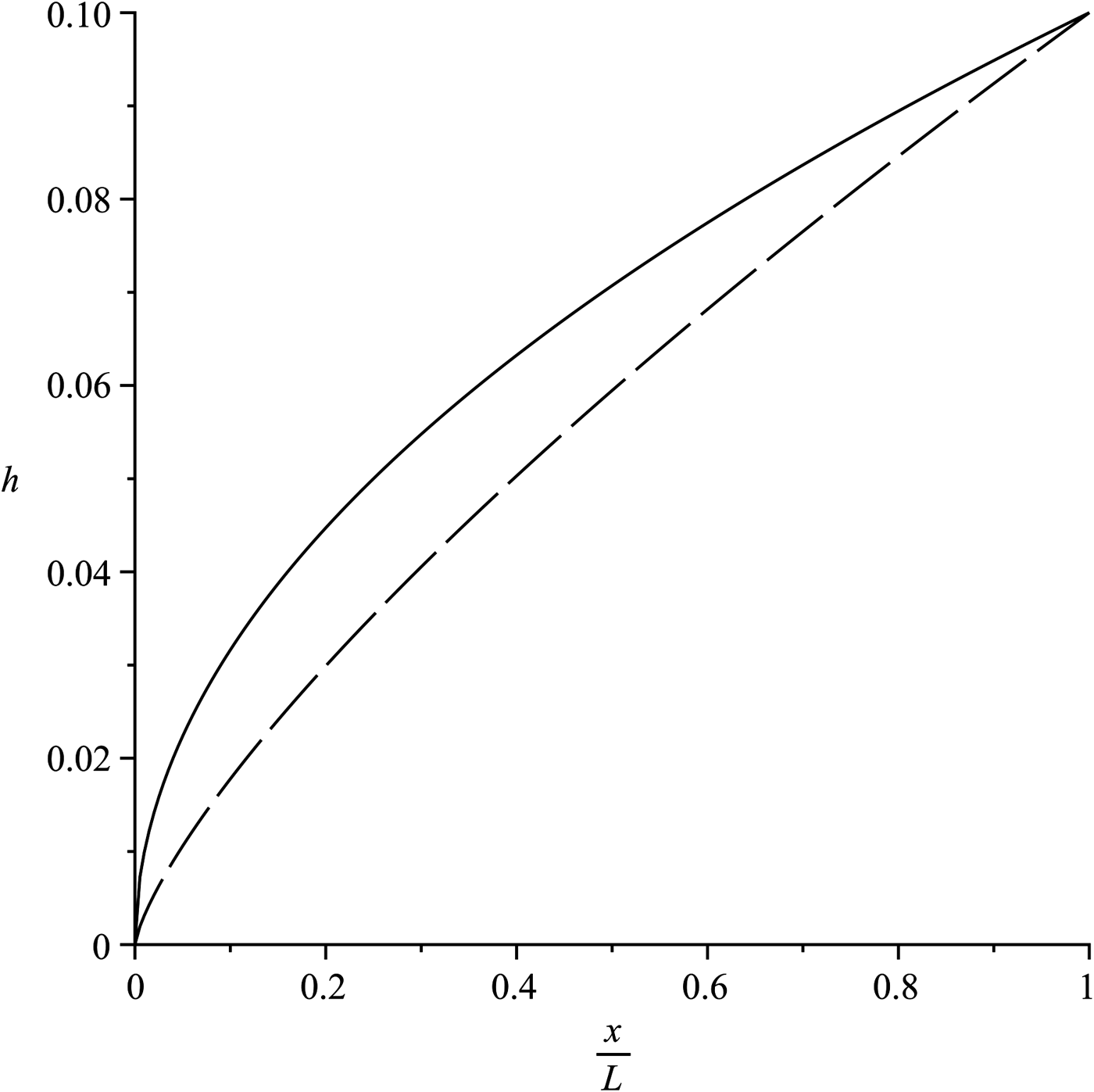
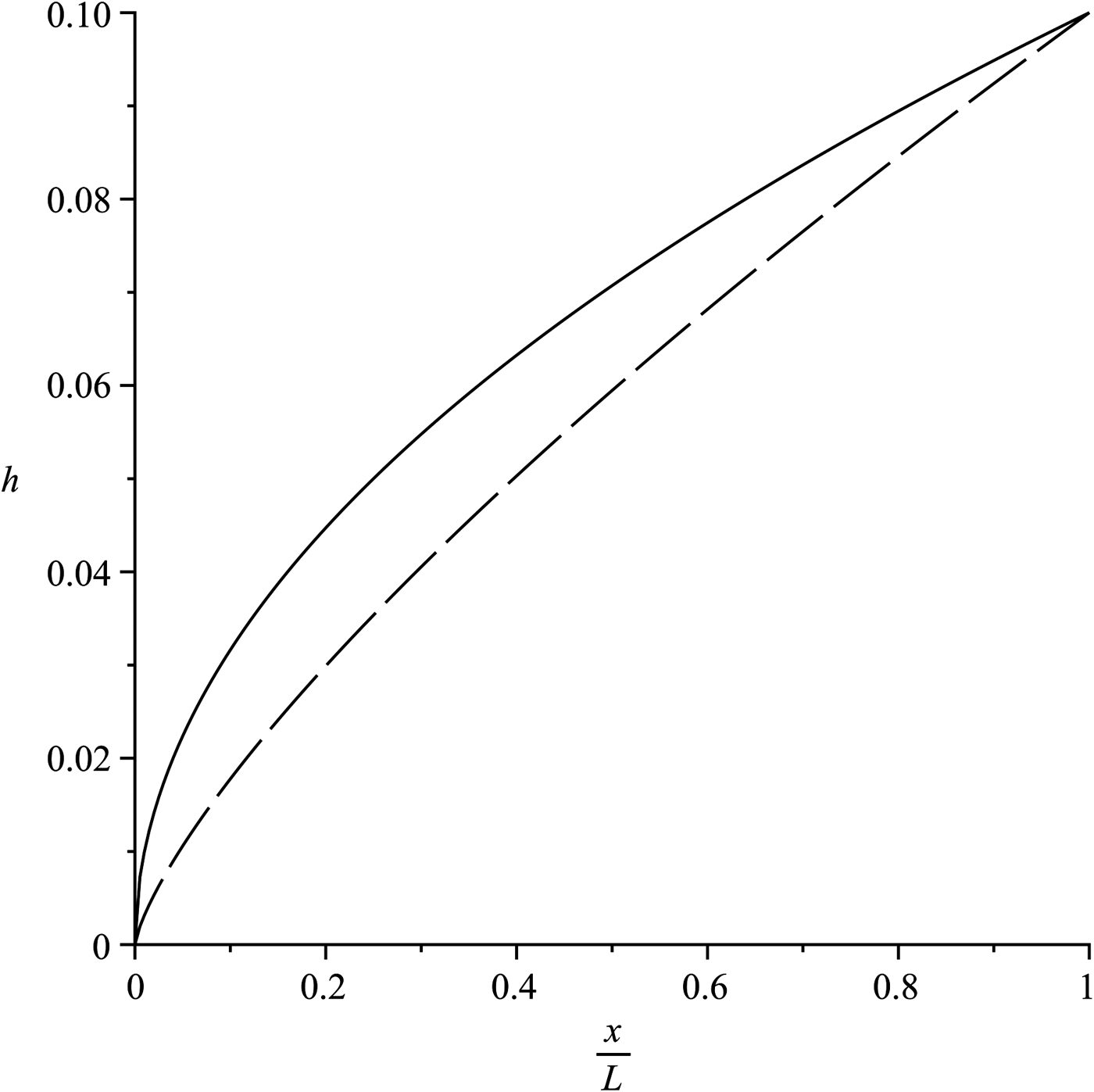
), this new profile reproduces the parabolic profile originally derived by Nye for plastic ice. Although this assumption is almost universally regarded as unphysical, a parabolic profile is nevertheless widely used in studies of both ice caps and glaciers (e.g. Benn and Hulton, Reference Benn and Hulton2010; Ng and others, Reference Ng, Barr and Clark2010). The solution Eqn (18) of the Vialov equation assuming Glen's law with n = 3 justifies this widespread use (Faraoni and Vokey, Reference Faraoni and Vokey2016) and agrees with the empirical value 1/2 of the exponent s for ice caps. It is important to be aware of the fact that this value of s is not tied to the unphysical assumption of perfectly plastic ice, as is instead widely believed.
$\sqrt L $
), this new profile reproduces the parabolic profile originally derived by Nye for plastic ice. Although this assumption is almost universally regarded as unphysical, a parabolic profile is nevertheless widely used in studies of both ice caps and glaciers (e.g. Benn and Hulton, Reference Benn and Hulton2010; Ng and others, Reference Ng, Barr and Clark2010). The solution Eqn (18) of the Vialov equation assuming Glen's law with n = 3 justifies this widespread use (Faraoni and Vokey, Reference Faraoni and Vokey2016) and agrees with the empirical value 1/2 of the exponent s for ice caps. It is important to be aware of the fact that this value of s is not tied to the unphysical assumption of perfectly plastic ice, as is instead widely believed.
-
• Böðvarsson's profile: This analytical longitudinal profile is derived from a model in which driving stress is balanced by sliding resistence. The profile is (Böðdvarsson, Reference Böðvarsson1955)
(20) $$h(x) = H\left[ {1 - {\left( {\displaystyle{x \over L}} \right)}^2} \right]$$
$$h(x) = H\left[ {1 - {\left( {\displaystyle{x \over L}} \right)}^2} \right]$$
with
where a and k are constants related to the mass-balance rate (through M = a(H − H 0)) and basal stress (through τ b = −kρghu) (Böðdvarsson, Reference Böðvarsson1955). Note that the ice thickness scales as H ∝ L 2. In this model, Eqn (8) with (m, n, q) = (0, 3, 1) gives s = 1/4 = 0.25. We conclude that the Bövarsson model is not a realistic description of ice caps longitudinal profiles.
-
• Bueler profile: In this longitudinal profile (Bueler, Reference Bueler2003; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005) the basal stress
 $\tau _{\rm b} = - \rho ghdh/{\rm d}x$
is finite at the ice terminus, contrary to the Vialov and other profiles. It is given in (Bueler, Reference Bueler2003; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005; Greve and Blatter, Reference Greve and Blatter2009):
(22)
$\tau _{\rm b} = - \rho ghdh/{\rm d}x$
is finite at the ice terminus, contrary to the Vialov and other profiles. It is given in (Bueler, Reference Bueler2003; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005; Greve and Blatter, Reference Greve and Blatter2009):
(22) $$h(x) = H\left[ {\left( {n + 1} \right)\displaystyle{x \over L} - n{\left( {\displaystyle{x \over L}} \right)}^{n + 1/n} + n{\left( {1 - \displaystyle{x \over L}} \right)}^{n + 1/n} - 1} \right]^{n/2(n + 2)},$$
(23)
$$h(x) = H\left[ {\left( {n + 1} \right)\displaystyle{x \over L} - n{\left( {\displaystyle{x \over L}} \right)}^{n + 1/n} + n{\left( {1 - \displaystyle{x \over L}} \right)}^{n + 1/n} - 1} \right]^{n/2(n + 2)},$$
(23) $$H = \left. {\left\{ {\displaystyle{2 \over n}} \right.{\left[ {\displaystyle{{\left( {n + 2} \right)\alpha} \over {2A}}} \right]}^{1/n}\displaystyle{1 \over {\rho g}}} \right]^{n/2(n + 1)}L^{n/2(n + 1)},$$
$$H = \left. {\left\{ {\displaystyle{2 \over n}} \right.{\left[ {\displaystyle{{\left( {n + 2} \right)\alpha} \over {2A}}} \right]}^{1/n}\displaystyle{1 \over {\rho g}}} \right]^{n/2(n + 1)}L^{n/2(n + 1)},$$
where α is a parameter appearing in the mass-balance rate (Bueler, Reference Bueler2003; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005)
 $$\dot b(x) = \alpha \left[ {{\left( {\displaystyle{x \over L}} \right)}^{1/n} + {\left( {1 - \displaystyle{x \over L}} \right)}^{1/n} - 1} \right]^{n - 1}. $$
$$\dot b(x) = \alpha \left[ {{\left( {\displaystyle{x \over L}} \right)}^{1/n} + {\left( {1 - \displaystyle{x \over L}} \right)}^{1/n} - 1} \right]^{n - 1}. $$
In this profile the maximum ice thickness scales as
for n = 3. The mass-balance rate Eqn (24) is not of the form c m x m and one cannot discuss the parameter m here. However, Eqn (8) can only agree with s = n/2(n + 1) if m = −1, which is unphysical. Therefore, the Bueler profile is not a reliable match of ice caps longitudinal profiles.
2.2. Glaciers
For glaciers, the parameter values (m, n, q) = (2, 3, 0.6) are believed to be appropriate (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). Equations (10) and (11) then give s = 3/5 = 0.60 and γ = 1.375, while the observed value is γ = 1.36 (Bahr and others, Reference Bahr, Pfeffer and Kaser2015). The theoretical models for longitudinal glacier profiles make the following predictions.
-
• Nye's parabolic profile: The longitudinal profile (Eqns (12) and (13)) for perfectly plastic ice predicts
 $H \propto \sqrt L $
and s = 0.5; hence this model seems inadequate to describe glaciers.
$H \propto \sqrt L $
and s = 0.5; hence this model seems inadequate to describe glaciers. -
• Vialov profile: For ice satisfying an n = 3 Glen law and for constant mass-balance rate, the Vialov profile, Eqns (14) and (15), again predicts s = 0.5. This model also seems inappropriate for glaciers.
-
• Power-law profiles: For mass-balance rate of ice described by Eqn (6), the new power-law profile obtained as an analytical solution of the Vialov equation by Faraoni and Vokey (Reference Faraoni and Vokey2016) is
(26) $$h(x) = H\left( {\displaystyle{x \over L}} \right)^s,\quad s = \displaystyle{{n + m + 1} \over {2(n + 1)}},$$
(27)
$$h(x) = H\left( {\displaystyle{x \over L}} \right)^s,\quad s = \displaystyle{{n + m + 1} \over {2(n + 1)}},$$
(27) $$H = \left[ {\left( {\displaystyle{{n + 2} \over {2A}}} \right) \displaystyle{{c_mL^{n + m + 1}} \over {{(\beta \rho g)}^n}}} \right]^{1/2(n + 1)} \equiv h_0L^s. $$
$$H = \left[ {\left( {\displaystyle{{n + 2} \over {2A}}} \right) \displaystyle{{c_mL^{n + m + 1}} \over {{(\beta \rho g)}^n}}} \right]^{1/2(n + 1)} \equiv h_0L^s. $$
These equations apply to large glaciers where the slope θ = h/l. Assuming (m, n, q) = (2, 3, 0.6) gives s = 3/4 = 0.75 and γ = 1.47. This value of γ does not coincide with the observed value γ = 1.36 but is close to the number 1.46 reported by Adhikari and Marshall (Reference Adhikari and Marshall2012) for a population of glaciers in steady state, in contrast with the value γ = 1.36 attributed by these authors to a state of glacier retreat causing greater reduction in V than in S. However, letting γ vary continuously while keeping c in Eqn (1) fixed, as done by Adhikari and Marshall (Reference Adhikari and Marshall2012), is inconsistent with the scaling theory of Bahr and others (Reference Bahr, Pfeffer and Kaser2015), as pointed out in this reference. Whether the numerical coincidence above is significant could be established by further analysis of the data.
-
• Böðvarsson's profile: Eqns (20) and (21) predict s = 2 which, together with n = 3 yields m = 12, ruling out this model for the description of glaciers.
-
• Bueler's profile: Eqns (22) and (23) has s = (n/2(n + 1)) = 0.375 for n = 3, which is reproduced only if m = −1. We conclude that the Bueler profile is also ruled out as a model of glaciers.
For glaciers, no known analytical model of longitudinal profile derived from theory fits well the volume/area scaling law. For ice caps, the theoretical model of Vialov for constant mass-balance rate and the new parabolic solution of Faraoni and Vokey (Reference Faraoni and Vokey2016) corresponding to m = 0 fit well the empirical data for the volume/area scaling law. The power-law profile Eqn (9) originally predicted with scaling analysis by Bahr and others (Reference Bahr, Pfeffer and Kaser2015) is reproduced only as an exact solution of the Vialov differential equation obtained by assuming the ice follows Glen's law in Faraoni and Vokey (Reference Faraoni and Vokey2016). The profiles, Eqns (18) and (16) are compared in Figure 1.
3. CONCLUSIONS
The volume/area scaling widely used, especially in relation to climate change, ice loss and sea-level rise, does not need to assume explicit models for the local ice thickness, i.e. the longitudinal glacier profile. Nevertheless, it is interesting to relate it to these models, thus connecting two branches of glaciology, which were, thus far, separated. Since the volume of a glacier or ice cap depends on its third-spatial dimension (the thickness), the empirical values obtained for the volume/area scaling law have implications for theoretical models of longitudinal glacier profiles. Assuming the ice thickness scales with length as [h] ~ [l] s , ice caps are well modelled by a parabolic profile, but this cannot come from the microphysical assumption of perfectly plastic ice, which is unrealistic. Instead, a parabolic profile can be obtained by the Vialov equation based on Glen's law for the behaviour of ice (Faraoni and Vokey, Reference Faraoni and Vokey2016). What is more, the power-law profile Eqn (16) obtained analytically by Faraoni and Vokey (Reference Faraoni and Vokey2016) reproduces the scaling exponent first predicted by scaling analysis by Bahr and others (Reference Bahr, Pfeffer and Kaser2015) for ice caps.
Contrary to ice caps, for valley glaciers no known theoretical solution of the ordinary differential equations describing longitudinal profiles fits well the empirical data on volume/area scaling. In any case, the volume/area scaling law Eqn (1) applies to ensembles of glaciers (i.e. to fictitious average glaciers and to other statistics of many glaciers) and it is not expected to apply to measurements of single, specific glaciers. The discrepancy noted here between theory and observations suggests that more accurate theoretical modeling of longitudinal profiles is needed for valley glaciers.
ACKNOWLEDGEMENTS
The author is grateful to David Bahr and to an anonymous referee for suggestions leading to significant improvements in the original manuscript. This work is supported by Bishop's University.