Towards Identification of Optimum Radar Parameters for Sea-Ice Monitoring

Abstract

Various field experiments have shown that microwave radars can be used to distinguish multi-year from first-year ice, although optimum radar parameters are not yet fully defined.

This paper presents the results from two theoretical models that, using selected physical parameters of sea ice, are able to predict the backscattering from multi-year and first-year ice under cold conditions. The possible ranges of the backscattering coefficient under various conditions (surface roughness, salinity, temperature, density, and air-bubble size) are calculated for multi-year and first-year ice by adjusting the parameters within the reported range of values.

Although the calculations show no specific resonance that would favor any particular frequency or incidence angles, the results confirm the experimental findings that Ku- and X-band frequencies, and incidence angles greater than 30°, are better for distinguishing sea-ice types than lower frequencies.

Résumé

Différentes expérimentations de terrain ont montré que les micro-ondes des radars pouvaient être utilisées pour distinguer les couches multi-annuelles et la glace de première année, bien que les paramètres radar les plus efficaces dans ce but ne soient pas encore complètement définis.

Cet article présente les résultats de modèles théoriques qui, en sélectionnant certains paramètres physiques de la glace de mer, sont capables de prévoir la dispersion par la glace multi-annuelle et par la glace de première année en conditions froides. Le domaine possible du coefficient de dispersion dans différentes conditions (rugosité, salinité, température, densité et tailles des bulles d’air) est calculé pour la glace multi-annuelle et pour la glace de l’année en ajustant les paramètres dans leur domaine de variation.

Bien que les calculs ne montrent pas de résonance spécifique qui favorise quelque fréquence ou quelques angles d’incidence particuliers, ils confirment les résultats expérimentaux qui montrent que les bandes fréquence Ku et X, ainsi que des angles d’incidence supérieure à environ 30° sont meilleurs que des fréquences plus basses pour distinguer les types de glace de mer.

Zusammenfassung

Verschiedene Feldversuche zeigten, dass Radar-Mikrowellen zur Unterscheidung mehrjährigen Eises von einjährigem benutzt werden können, obwohl die optimalen Radar-Parameter noch nicht völlig bestimmt sind.

Dieser Beitrag enthält Ergebnisse von zwei theoretischen Modellen, die in der Lage sind, aus ausgewählten physikalischen Parametern für Meereis die Rückstreuung sowohl für mehrjähriges wie für einjähriges Eis unter kalten Bedingungen vorherzusagen. Die möglichen Bereiche des Rückstreuungskoeffizienten unter verschiedenen Bedingungen (Oberflächenrauhigkeit, Salzgehalt, Temperatur, Dichte, Luftblasengrösse) werden für mehr- und einjähriges Eis durch Anpassung der Parameter innerhalb bekannter Wertebereiche berechnet.

Obwohl die Berechnungen keine spezifische Resonanz zeigen, die eine bestimmte Frequenz oder einen Einfallswinkel bevorzugen würde, erhärtet das Ergebnis die experimentellen Feststellungen, wonach Ku- und X-Band-Frequenzen und Einfallswinkel grösser als 30° für die Unterscheidung von Meereistypen besser sind als niedrige Frequenzen.

Introduction

Sea ice is a very dynamic medium. There are many kinds of ice with different growth histories, whose surface conditions and shapes change continuously during the various stages of growth. There are also spatial and temporal variations in snow-cover thickness and surface roughness.

Over the last 15 years, sea-ice microwave signatures (both active and passive) have been gathered, under various conditions, during the course of several expeditions. Although most of the active microwave sensors used in these experiments were not specifically designed for sea-ice monitoring, they were found capable of: (1) ice-type identification, (2) detection of icebergs, (3) location of ice–water boundaries, and (4) measurement of ice deformation, etc. (Luther and others, 1982).

This paper is an attempt to define an optimum set of radar parameters (frequency, incidence angle, and polarization) for identification of multi-year and first-year ice under cold conditions. For a spaceborne imaging radar (SAR), the resolution and swath-width must also be determined but, since these factors depend on user requirements, they are not considered here.

A few attempts have been made to explain, theoretically, radar backscatter from sea ice using models based on simplified physical and electrical characteristics (Fung and Eom, 1982; Parashar, unpublished). These models suffer from the dearth of surface measurements in earlier experiments used as comparisons. Kim (unpublished) showed that surface scattering may be the dominant backscattering mechanism for first-year ice and that the physical-optics model (Ulaby and others, 1982), using an exponential correlation function, can predict the microwave signatures of first-year ice. For multi-year ice, the volume-scattering model based on radiative-transfer theory (Chandrasekhar, 1960) can describe the backscattering for frequencies higher than about 10 GHz but the surface-scattering contribution has to be included for lower frequencies. It was shown (Kim, unpublished) that a simple semi-empirical model is a good approximation to the complicated radiative-transfer model in describing the volume scattering from multi-year ice.

Several models (for both surface- and volume-scattering) describing radar backscatter from distributed targets have been reported (Ruck and others, 1970, p. 671–772; Ulaby and others, 1982). In the physical-optics model (widely used in surface-scattering theories), the Kirchhoff surface integral is simplified using either the stationary-phase or scalar approximation. The validity condition for the stationary-phase approximation is that the radius of curvature at all points must be larger than a wavelength. If the standard deviation is small or comparable to the wavelength, the scalar approximation may be used to compute the backscatter (Beckmann and Spizzichino, 1963; Ulaby and others, 1982).

Many natural or Man-made materials can be modeled as continuous media with random dielectric fluctuations or as collections of scatterers distributed randomly in a lossy dielectric. Two approaches that may be used to determine wave scattering and emission from volumes of such media are the intensity approach and the field approach. The intensity approach (radiative-transfer theory) is based on Boltzmann’s equation. Here, the phase interference, or correlation, between different fields is ignored and power is added incoherently. The field approach is based on solving the wave equation and taking into account the scattering and absorption characteristics of the medium. The semi-empirical model used in this paper to describe the volume scattering from sea ice is based on the intensity approach.

The physical-optics (surface-scatter) model under the scalar approximation is used alone to calculate the ranges of the radar-scattering coefficient, σ^o, for first-year ice (young and grey ice are not considered in this paper), and, in combination with the semi-empirical (volume-scatter) model based on the intensity approach, to calculate the ranges of σ^o for multi-year ice for different values of surface roughness, salinity, density, air-bubble size, and temperature. The results do not indicate resonance at any particular frequency or incidence angle but confirm the experimental findings that Ku- and X-band frequencies, and incidence angles greater than 30°, can discriminate between cold first-year and multi-year ice better than lower frequencies and smaller incidence angles.

Summary of Experimental Results

During the last 15 years, several experiments were conducted to determine the optimum radar parameters for differentiating multi-year from first-year ice. These experiments used surface-based and airborne scatterometers as well as airborne imaging radars (both real and synthetic aperture). A brief summary of the results is given below.

Frequency

It has been reported (Ramseier and Lapp, 1981; Luther and others, 1982) that radar images at X-band or higher frequencies are better than L-band frequencies to differentiate ice types under cold conditions. L-band (near 1 GHz) images provide little or no distinction between first-year and multi-year ice; radars in this band are believed to respond only to gross surface features. C-band (near 5 GHz) images appear more like those at X-band than like those at L-band (Luther and others, 1982).).

Parashar (unpublished) reported that a frequency of 13.3 GHz was better than 400 MHz for discriminating multi-year ice from thinner types of sea ice, Multi-frequency scatterometer measurements also show (Onstott and others, 1979) that radars at L-band frequencies do not have the capability to discriminate multi-year from first-year ice. One set of reported measurements showed that 9 GHz is the best of the frequencies between 8–18 GHz and 1.5 GHz (Onstott and others, 1982).

Measurements of radar backscatter from sea ice under fall conditions were made near Mould Bay, N.W.T., Canada, during October 1981 at frequencies between 4 and 18 GHz, and incidence angles between 10° and 70° with like- and cross-polarizations (Onstott and others, 1984). The results indicate that radars at X- and Ku-band frequencies have similar capabilities to differentiate multi-year from grey-white ice and are a little better than radars at C-band frequencies. The difference in the scattering coefficient of first-year and multi-year ice was largest at Ku-band frequencies. The primary conclusion is that X- and Ku-bands are much better than L-band, and somewhat better than C-band, for differentiating multi-year from younger ice (Luther and others, 1982).

Incidence angle

Incidence angles greater than 20° (Seasat incidence angle) are recommended to minimize the ambiguity between open water and ice. Incidence angles smaller than 80° are recommended because topography may dominate the backscatter at shallow depression angles (Gray and others, [1977][a]; Ramseier and Lapp, 1981).

The difference in σ^o between multi-year and first-year ice based on airborne scatterometer measurements increased up to about 30° and remained constant beyond that angle (Gray and others, [1977][b]). Angles from 20° to 40° were found to be best with VV polarization (Onstott and others, 1979), and angles between 40° and 60° were better for discriminating multi-year from grey and first-year ice (Onstott and others, 1984). However, Guindon and others (1982) reported that all scatterometer angles between 8° and 55° give the same classification accuracy in the absence of open water. Airborne scatterometer measurements at 13.3 GHz reported by Parashar (unpublished) indicate that incidence angles greater than 25° are better for discriminating multi-year from first-year ice. In summary, incidence angles between 20° and 80° are usually recommended but some measurements show that angles between 30° and 60° are better.

Polarization

Cross-polarized images usually give more grey-scale information but new-ice forms are harder to identify than with like-polarization (Gray and others, [1977][b]). The differences between the σ^O values for multi-year and first-year ice are usually larger for cross- than for like-polarization at X- and Ku-band frequencies (Gray and others, [1977][a], 1982; Onstott and others, 1979 Hawkins and others, 1981), although one report (Guindon and others, 1982) indicated that there was no evidence favoring any particular polarization in classification accuracy. The usual conclusion is that, although cross-polarization has a little better capability than like-polarization, it does not justify the added cost and complexity (Luther and others, 1982).

Backscatter Model of Sea Ice

Kim (unpublished) showed that surface scattering was the dominant backscattering mechanism for first-year ice and volume scattering was dominant for multi-year ice for frequencies higher than about X-band. The surface-scattering contribution had to be included for lower frequencies to explain the backscatter data from multi-year ice.

Surface scattering from sea ice was computed using the physical-optics model with an exponential correlation function. The correlation function is given by

(1)

The detailed derivation for the scattering coefficient with the exponential correlation function under the scalar approximation is available in Eom (unpublished) and the simplified expression for the scattering coefficient is

(2)

where k = wave number in the upper medium, R _pp = Fresnel reflection coefficient, σ = surface-height standard deviation, l = correlation length, θ = angle of incidence, and p = polarization (V or H).

This model is applicable to surfaces for average radius of curvature r_c > λ, and r.m.s. slope of the surface m < 0.25 (Ulaby and others, 1982).

The requirements for this model were satisfied by the measured surface-roughness parameters for frequencies between 4 and 18 GHz; the calculated correlation function did, indeed, show exponentially decaying behavior. This model, using measured values of l and σ, provided a good fit to measured angular and frequency responses of the backscattering coefficient of first-year ice for the October 1981 experiment.

Neglecting the volume and surface interactions, the scattering coefficient of the multi-year ice can be expressed as

(3)

where σ_s ^o(θ) = scattering coefficient of the ice surface, T(θ) = power transmission coefficient of the upper ice surface,

= volume-backscattering coefficient of the ice, and θ’ = angle of the refraction in the ice medium.

The volume-scattering model selected was a semi-empirical version, which was simplified from the general theoretical solution of the radiative-transfer model (Karam and Fung, 1982; Eom, unpublished). The volume-scattering component is calculated by assuming that the air bubbles are spherical, of equal size, and distributed uniformly, as shown in Figure 1. The volume-backscattering coefficient is given by

(4)

where N = number of scatterers per unit volume, σ_b = backscattering cross-section of a single particle, k _e = volume extinction coefficient, L(θ’) = exp(k _e d sec(θ’)), and d = depth of the layer.

Fig. 1. Snow-free multi-year ice model.

A derivation of this expression for the volume-backscattering coefficient is available in Ulaby and others (1982).

The surface-scattering term of Equation (3) was calculated using the physical-optics model with exponential correlation function. The volume-scattering term was calculated using Equation (4). Agreement between measured and predicted angular and frequency responses of σ° for multi-year ice was fairly good. Because the bubble-size distribution was not measured, the parameters were selected to agree with the measured values at 5 GHz. These parameters were then used for theoretical modeling at all other frequencies.

For first-year ice, the surface-scattering term,

, usually dominates. For multi-year ice, the volume-scattering term,

, is usually bigger than the surface-scattering term and decreases rapidly as frequency is decreased. It is possible, even with multi-year ice, for the volume-scattering term to be smaller than the surface-scattering term at lower frequencies. The frequency at which the dominance changes is determined by the incidence angle and the surface roughness. Examples are shown in Figure 2 for smooth and rough multi-year ice. When the ice surface is rough, the surface-scattering term is bigger than the volume-scattering term below about 8 GHz.

Fig. 2. Two examples of theoretical frequency behavior of σ^O. Surface-scattering term and volume-scattering terms are plotted separately for two kinds of surface roughness. σ is standard deviation of height and l is the correlation length.

Figures 3 and 4 show typical predicted frequency and angular behaviors of σ° for multi-year and first-year ice, calculated using the physical-optics model for surface scattering and the semi-empirical model for volume scattering. Also shown are data taken during the fall 1981 expedition. No surface-parameter measurements were made on this floe (composite multi-year ice) (Onstott and others, 1984); the model parameters were selected arbitrarily within typical reported values to match the data at the lowest frequency (5 GHz). Even though the model parameters were not optimized in any sense, good general agreement can be seen in Figures 3 and 4 in both the frequency and angular behaviors. Note that the curves for multi-year ice include both surface- and volume-scattering contributions, while the curves for first-year ice include only the surface-scattering term.

Fig. 3. Typical frequency behaviors of multi-year ice and first-year ice predicted by theoretical models. The model parameters were adjusted to match the data shown.

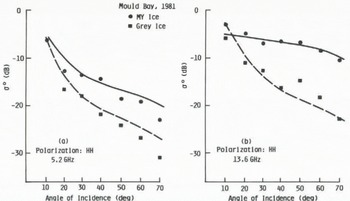
Fig. 4. Theoretical angular variations of σ^O of multi-year ice and first-year ice. The model parameters and experimental data are the same as those used in Figure 3.

Model behavior

The ranges of σ^o for multi-year and first-year ice were calculated by adjusting the model parameters within the reported ranges of values. From these ranges of σ^o, optimum radar parameters for sea-ice monitoring of two major ice types were defined to the extent possible with present knowledge.

As temperature changes, the dielectric constant of sea ice changes, although the exact dependence has yet to be determined. The temperature change also causes a change in the Fresnel reflection coefficient, resulting in a variation of σ^O of about 3 dB (Kim, unpublished). The change in the imaginary part of the dielectric constant due to temperature variation causes the volume-scattering characteristics of multi-year ice to change. The σ^O of multi-year ice can vary by as much as 6 dB (Kim, unpublished) under different temperature conditions.

The small-scale surface roughness plays an important role in determining the σ^O of first-year as well as multi-year ice. Both the density and size of air bubbles in multi-year ice have a significant impact on σ^O (< 3 dB and < 10 dB, respectively).

Frequency. Figure 5 shows the ranges of theoretical σ^O for multi-year and first-year ice under various conditions. The selected limiting values of the parameters are shown in the caption of this and subsequent figures. The lowest curve (1) is for smooth-surfaced first-year ice when salinity and temperature are low. As either the salinity or temperature increases, the dielectric constant increases. The next curve (2) is for first-year ice with a medium-rough surface and increased salinity and temperature. Curve (3) is for multi-year ice with a medium-rough surface and small air bubbles when the temperature is low. The highest curve (4) is for rough-surface multi-year ice with larger air bubbles and zero salinity, which cause a larger volume-scattering contribution due to decreased absorption loss.

Fig. 5. Theoretical σ^O for multi-year ice and first-year ice for θ = 40°. The ranges of values illustrated represent various limiting cases for model parameters.

• First year ice: (1) smooth (σ = 0.15. l = 8.9 cm), S = 8°/₀₀, T = −25° C; (2) medium rough (σ = 0.37. l = 8.5 cm), S = 10°/₀₀. T = −15 ° C.

• Multi-year ice: (3) medium-rough surface (σ = 0.37, l = 8.5 cm), S = 0.6°/₀₀, T = −20° C, ρ = 0.75 g/cm³, air-bubble diameter = 1.6 mm, bubble layer = 20 cm. (4) rough surface (σ = 0.81, l = 8.2 cm), S = 0°/₀₀, T = −15° C, ρ = 0.75 g/cm³, air-bubble diameter = 2 mm, bubble layer = 50 cm.

The effect of higher temperatures is to increase the σ° of first-year ice (surface scattering dominant) and to decrease the σ^O of multi-year ice (volume scattering dominant for frequencies higher than about X-band. Therefore, as temperatures increase, the difference in σ^O between first-year and multi-year ice decreases.

Figure 5 shows that, for nearly all frequencies considered, there is a difference in σ^O between multi-year and first-year ice. It can also be seen that higher frequencies give better discrimination.

In Figure 6 the model parameters are further varied to include very rough first-year ice with high salinity and temperature (curve (2)). Lossier multi-year ice with higher salinity and temperature than in curve (3) of Figure 5 is shown as curve (3) of Figure 6; multi-year ice with a rough surface, larger air bubbles, and zero salinity is plotted as curve (4) of Figure 6. In these cases, a large overlap between the σ^O values for first-year and multi-year ice can be seen except above 17 GHz. Unless the frequency is high enough, there can be confusion between first-year ice with a very rough surface and multi-year ice with small air bubbles, since surface roughness is the major factor in determining the σ^O of first-year ice.

Fig. 6. Theoretical σ^O for multi-year ice and first-year ice for θ = 40°. The ranges of values illustrated represent various limiting cases for parameters.

• First-year ice: (1) smooth (σ = 0.15, l = 8.9 cm), S = 8°/₀₀, T = – 25° C; (2) rough (σ = 0.81. l = 8.2 cm), S = 12‰, T = –5° C.

• Multi-year ice: (3) medium-rough surface (σ = 0.37, l = 8.5 cm), S = 0.7°/₀₀, T = –5°C, ρ = 0.75 g/cm³, air-bubble diameter = 1.6 mm, bubble layer = 20 cm; (4) rough surface (σ = 0.81, l= 8.2 cm), S = 0‰, T = –5° C, ρ = 075g/cm³, air-bubble diameter = 2.5 mm, bubble layer = 50 cm.

In Figure 6 the model parameters are further varied to include very rough first-year ice with high salinity and temperature (curve (2)). Lossier multi-year ice with higher salinity and temperature than in curve (3) of Figure 5 is shown as curve (3) of Figure 6; multi-year ice with a rough surface, larger air bubbles, and zero salinity is plotted as curve (4) of Figure 6. In these cases, a large overlap between the σ^O values for first-year and multi-year ice can be seen except above 17 GHz. Unless the frequency is high enough, there can be confusion between first-year ice with a very rough surface and multi-year ice with small air bubbles, since surface roughness is the major factor in determining the σ^O of first-year ice.

In no sense are the ranges shown in Figure 6 the absolute ranges of σ^O for multi-year and first-year ice. Only small-scale roughness (surface-height standard deviation less than a wavelength) was considered, and the effect of large-scale roughness (larger than a wavelength) caused by ridges, hummocks and melt ponds was neglected. The full ranges of surface roughness for multi-year and first-year ice have never been determined. Moreover, the distribution of sizes of air bubbles is in question. Temperatures above −5° C, where the dielectric constant of sea ice increases rapidly, were not considered.

The presence of snow-cover increases the backscatter from smooth first-year ice, resulting in a rise in the overall level of curves labeled (1) in Figures 5 and 6. The effect of snow-cover is more pronounced at higher frequencies (Onstott and others, 1979) but the influence of snow-cover on frequency response of σ^O has not been established.

With all of these limitations, and for surface temperatures lower than −5° C, higher frequencies can be stated to be better than lower ones in discriminating multi-year from first-year ice.

Incidence angle. The theoretical angular response of multi-year and first-year ice at 5 and 15 GHz is shown in Figure 7. The σ^O of first-year ice decreases rapidly with increasing incidence angle but that of multi-year ice decays more slowly because of the presence of volume scattering. Therefore, in terms of discrimination capability, incidence angles greater than 30° or 40° are to be preferred.

Fig. 7. Theoretical angular variations of σ^O of multi-year ice and first-year ice. The model parameters are the same as those used in Figure 5.

As the model parameters are varied further to include very rough first-year and lossier multi-year ice, the overlap between scattering from the two ice types occurs for all the incidence angles, as illustrated in Figure 8. The theoretical model bounds all the measurements shown except one. As mentioned in the previous section, the boundaries are not the absolute limits and further study is needed. However, the fact that all first-year-ice measurements at incidence angles greater than 10° lie below the lowest multi-year-ice measurements is encouraging.

Fig. 8. Theoretical boundaries of σ^O for multi-year ice and first-year ice. The model parameters are the same as those used in Figure 6, Several reported measurements are shown. Except for Gray’s (1982) case of multi-year ice, all lie within the boundaries. Solid points are first-year ice.

Polarization. Both the radiative transfer and semi-empirical volume-scatter models predict a slightly higher

than

for multi-year ice; the physical-optics model under scalar approximation predicts a lower

than

, because of the Brewster angle effect. According to these models, VV-polarization should be better for discrimination than HH-polarization. However, since the measurements do not always show that kind of behavior, the limitations of these theoretical models can be seen.

The radiative-transfer volume-scatter model can explain the cross-polarized σ^O for multi-year ice (Kim, unpublished),

is zero for the physical-optics model unless multiple scattering is considered. Therefore, a quantitative comparison of the capabilities of like- and cross-polarizations could not be made. Since the cross-polarized component in surface scattering (first-year ice) is a second-order term, cross-polarization should be better than like-polarization in distinguishing multi-year from first-year ice. The cross-polarized σ^O for multi-year ice is only about 10 dB lower than like-polarized σ^O at 13 GHz and 40° incidence angle (Gray and others, [1977][a]; Onstott and others, 1979). It, therefore, could be used to distinguish multi-year ice from its surroundings without requiring a large dynamic range.

Conclusions

This paper provides a summary of experimental findings reported to date and, using a reasonable set of model parameters, compares them with theoretical models that match the data sets. By adjusting, within reported ranges, the model parameters for σ^O, roughness, and air-bubble size, the possible ranges of σ° for multi-year and first-year ice are calculated. This shows that the best radar parameters for sea-ice monitoring are: (1) X- or Ku-band frequencies (higher frequencies were not considered), and (2) incidence angles equal to or greater than 30°. No specific resonances were found that might favor any frequency or incidence angle. The theoretical findings agree with the general experimental conclusions.

The optimum polarization could not be selected. This was due in part to the lack of reliable cross-polarized data for the whole frequency range considered, and in part to the inability of the first-order surface-scattering model to explain the polarization dependence of backscatter from sea ice.

The theoretical calculations and models presented in this paper were restricted to surface temperatures below −5°C, so the models are not expected to be valid during the melt season, when ice properties change drastically.

The physical and electrical characteristics of ice and snow need further study in order to refine the models. The important parameters should be: (1) the ranges of values of small-scale roughness for multi-year and thinner types of sea ice; (2) the behavior of the dielectric constant (especially the imaginary part) or the upper parts of multi-year ice; and (3) the distribution of air-bubble diameters in the various layers of multi-year ice found in different areas of the Arctic.