Shear-wave detection of asymmetric c-axis fabrics in the GISP2 ice core, Greenland

Abstract

c-axis fabrics of the GISP2 ice core from central Greenland have been measured rapidly and accurately in the field, using both compressional and shear waves generated by an inexpensive, commercially available, “idiot-proof” device. Compressional-wave data were collected at 10 m intervals for the upper 2250 m of the ice sheet and show progressive clustering of c axes toward the vertical with increasing depth but no large steps at climatic boundaries in the core. The degree of clustering measured by ultrasound agrees closely with that measured using traditional optical techniques but the ultrasound technique is easier and faster than optical methods. A slight asymmetry in the c-axis clustering is revealed by the shear-wave data and increases with increasing depth, indicating that deformation is not symmetric about the vertical at the site.

1 Introduction

c-axis fabrics are important in dynamic glaciology. A “soft” fabric may deform an order of magnitude more rapidly than a “hard” one under a given stress state (e.g. Budd and Jacka, 1989), the fabric may record the cumulative strain and stress state that produced it (e.g. Azuma and Higashi, 1985; Alley, 1988) and the fabric may provide information on the microphysical processes of deformation (e.g. Alley, 1992). The ability to understand and model fabrics is imperfect but improving (e.g. Azuma and Higashi, 1985; Alley, 1988; Lipenkov and others, 1989; Van der Veen and Whillans, 1994).

In the upper parts of cold ice sheets, the symmetry of the f-axis fabric is simply related to the symmetry of the stress state that produced it. Theory and observation agree that flow from the peak of an ice dome will produce a c-axis fabric symmetrical about the vertical; flank flow will cause the c-axes to cluster more tightly toward the vertical in the flow direction than in the transverse direction, although the degree of rotational asymmetry in the clustering is not reproduced well in the theory (Alley, 1988). If quantitative agreement could be obtained between theory and model, it might be possible to test for stability of dome position by measuring rotational asymmetry of fabrics in ice cores on and near domes; dome migration should disrupt the expected pattern of rotational symmetry near the dome and asymmetry away from it.

One problem with studies of this sort is the sparse data base. Optical (universal-stage) measurements of c-axis fabrics are time-intensive but typically collect only enough data to characterize the degree of clustering of the c axes. Measurement of subtle azimuthal variation in degree of clustering would require significantly more time and effort. Compressional-wave (P-wave) ultrasound techniques (e.g. Kohnen and Gow, 1979) provide a useful and largely non-destructive way of measuring the degree of c-axis clustering when it is nearly symmetrical about the core axis; the difference in sonic velocity between the vertical and horizontal directions is a function of the intensity of clustering. Such a measurement with our instrument requires that flat and parallel surfaces be prepared for sonic transducers. To search for azimuthal variation in clustering, multiple pairs of flat surfaces would be required around the core, increasing the core loss and the time required for the measurement. An alternative technique developed by Langway and others (1988) required machining the core to precise tolerances on a lathe and then measuring azimuthal variations, again requiring significant time, effort and core loss.

A possible solution to this dilemma is to use shear waves propagated along the core axis. Because shear waves vibrate perpendicular to the propagation direction, those traveling along the core axis sample the degree of clustering toward the vertical. By simply rotating the shear-wave source on the end of the core, the degree of clustering can be measured as a function of azimuth, providing a rapid, non-destructive and accurate measurement of the asymmetry of the fabric. We show that measuring two orthogonal orientations determines the asymmetry in clustering to an accuracy of 80%.

To test this possibility, we conducted a series of shear-wave experiments on core samples collected during the 1992 field season from the Greenland Ice Sheet Project II (GISP2) deep core. As reported below, we find that we can detect a small azimuthal asymmetry in the c-axis fabrics, especially in the deeper ice. Our apparatus was not optimized for these measurements and we anticipate significant improvement in data quality in future measurements. We present our preliminary results here to demonstrate the potential power of the method and to urge other investigators to collect similar data from other ice cores, helping to build the large data base needed to address questions on ice deformation.

One model for fabric-induced seismic anisotropy assumes that all the c axes are uniformly and randomly distributed within a cone of half-angle I (the so-called “solid-cone” model) (Bennett, 1968). The solid-cone assumption is justified because the universal-stage measurements show that the c axes are indeed distributed around the interior of a cone rather than clustered on the surface (the so-called “surface-cone” model). By comparing the longitudinal and transverse compressional-wave velocities, we solve for this half-angle I.

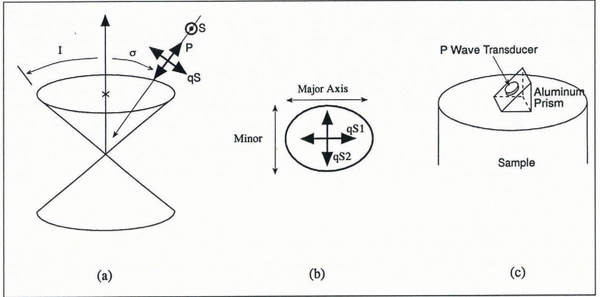
The geometry of this model is illustrated in Figure 1a. The cone half-angle is I and the propagation angle σ is the angle between the propagation direction of the ultrasound energy and the cone axis. The three phases of ultrasound propagation, P, qS and S, are also illustrated by their particle motion. The pure shear wave (S) vibrates perpendicular to the plane defined by the propagation direction and the fabric symmetry axis. The quasi-shear wave (qS) vibrates in this plane but with particle motion perpendicular to the propagation direction.

Fig. 1. (a) Cone of c axes with cone half-angle I and propagation angle σ indicated. P-, qS-and S-wave particle motions are indicated by the arrows, (b) Horizontal cross-section of an elliptical cone, (c) Schematic of shear-wave generation. The P-wave transducer was attacked to the aluminum prism to produce shear waves at the prism/sample interface.

If the ice has experienced flank flow, we assume the asymmetry of the c-axis fabric will be elliptical; that is, the horizontal cross-section of the cone will be an ellipse rather than a circle. Then, qS waves propagating along the axis of symmetry, but with displacement in the direction of, say, the semi-major axis, will travel at a velocity appropriate to an apparent circular cone whose half-angle I equals the width of the semi-major axis. Rotating the transducer by 90° causes the qS waves to travel at a velocity appropriate to an apparent circular cone whose half-angle I equals the width of the semi-minor axis. We represent these experiments in Figure 1b.

2. Instruments and Methods

2.1. Instrumentation

A commercial flaw-detector (the Epoch-2000^TM manufactured by Panametrics Inc.) with a built-in oscilloscope display was used to produce the transmit pulse and view the received pulse. All controls and record parameters were adjustable from the front panel; these include source power, gain, time-scale and travel-time picking. Two important features of the unit that were crucial for accurate and repeatable results were the adjustable-gain display and the autopick facility. The gain was adjusted such that the received pulse was at exactly 80% of some predetermined reference level. The Epoch-2000 would then automatically pick the time at which the pulse had achieved three-quarters of its peak. Because of the consistency of pulse shape and rise time, the travel-time picks were unaffected by attenuation. This 75% level was calibrated on an aluminum rod of known length and velocity to determine the fixed delay introduced by cables, transducers and the rise time of the pulse to its pick level.

Finally, the sample thickness could be entered into the unit and the velocity calculated. This facility was important as a quick check on the validity and reproducibility of the measurements. The completely self-contained unit was modified to operate at low temperatures. The unit worked reliably every field season for a number of different operators and resulted in consistent and repeatable data.

The sample was prepared by cutting parallel faces on opposite sides of the sample and sanding them fiat. Due to the lack of azimuthal information on the core sample, the transverse measurements are at arbitrary azimuthal orientations. The length, l, of the sample was measured with Mitutoyo electronic calipers that have a precision of ±0.01 mm. Each sample was measured three times and averaged. In general, in the longitudinal direction, l ≈ 110 mm, and in the transverse direction, l ≈ 120 mm. We estimate the uncertainty in l at δl = ±0.1 mm.

The experiment was conducted in two parts: compressional-wave (P-wave) transmission and quasi-shear-wave (qS) transmission. The P waves were used in two directions: ray paths along the axis of the ice core (longitudinal) and transverse to the axis (transverse). The source for all the experiments was a 2.25 MHz pulsed transmitter coupled to a 2.5 cm circular flat transducer.

For the qS experiments, we attached the transducer to a prism-shaped block of aluminum, thus producing shear waves at the aluminum-ice interface (Fig. 1c). Two shear-wave experiments (with orthogonal particle-displacement directions) were conducted in the longitudinal direction.

The travel time was measured in two ways. For the P-wave experiments, the signal-to-noise ratio (SNR) of the raw pulse was sufficiently high (60-100 dB) that accurate picks of the received pulse could be made on the oscilloscope screen. For these data, we estimate the travel-time measurement accuracy δt=± 0.05 μ. For the shear-wave data, the SNR was lower and the waveform was recorded digitally and analyzed later. We discuss that analysis path in the next section.

The velocity and velocity errors are

(1)

(2)

respectively, where l is the distance between transducers and t is the travel time. The velocity uncertainty δV is related to the measurement errors δ1 and δt in length and travel time, respectively.

2.2. Shear waves

The shear-wave receive waveforms were recorded on a digital storage oscilloscope at a sample interval of 0.05 μs. Limited storage in the oscilloscope restricted us to two measurements in each polarization. Analysis of the shear-wave data consisted of first band-pass filtering the waveforms to the bandwidth of the transducers and then deconvolving the waveform with the transmit wavelet (e.g. Yilmaz, 1987). Deconvolution is a procedure for compressing a wavelet and improving the temporal resolution of a signal.

The two orthogonal qS waveforms thus produced were displayed and the arrivals picked using the public-domain program SAC (Seismic Analysis Code) (Tull, 1989). Because the SNR of the shear-wave arrivals was small (3-12 dB), it was often difficult to identify corresponding phases of shear-wave arrivals in the orthogonal waveforms. In some cases, the shear-wave arrival was strong in only one of the two signals. In these cases, the two waveforms were cross-correlated and the lag of the cross-correlation peak is the travel-time difference between the two orthogonal shear-wave transmissions. The size of the cross-correlation peak is an approximate measure of the uncertainty in the travel-time difference picks of the two orthogonal phases. A large cross-correlation peak implies a good match between the two waveforms.

An 8μs Hanning window was applied around the arrival time to reduce unwanted high-frequency oscillations in the cross-correlation process (Papoulis, 1984). A Hanning window rises from zero at the beginning of the window to 1 at the center and then falls back to zero at the end. It has the form of a cosine function.

3. Results

To determine the fabric from ultrasound velocity measurements, we use a forward model that predicts velocities for various c-axis distributions (Bennett, 1968; Blankenship and Bentley, 1987; Blankenship, 1989). The general form of the slowness S (inverse of velocity) through a conical distribution of c axes is

(3)

(4)

(5)

(6)

where i = 1, 2, 3 refer to either compressional waves (P), shear waves where the plane of particle motion includes the symmetry axis (qS) and shear waves where the plane of particle motion is perpendicular to the symmetry axis (S), respectively (see also Crampin, 1981). The K_j are functions of the elastic properties of ice. Equation (4) for A⁽ⁱ⁾(I, T) contains a linear bias term S⁽ⁱ⁾ related to sample temperature T. The angle between the energy propagation direction and the symmetry axis of the anisotropy is σ.

3.1. Compressional waves

Figure 2 is a plot of the theoretical P velocities in the longitudinal (σ = 0) and transverse (σ = π/2) directions as functions of half-angle I at temperature T =-10 ; c. We solve for I by fitting the measured velocity difference Δv_p = v _p (long)-v _p (trans) to the theoretical values. We measured the surface temperature of the samples before making a velocity measurement. However, we believe there is high uncertainty (±2°C) about this, because the samples were analyzed as soon as possible after they emerged from the drill. Thus, the temperature might not have stabilized. The in-situ temperature for ice depth Z = 1500 m is about T = −32°C (personal communication from G. Clow, 1992). The temperature in the laboratory was between T = −23°C and T = −28°C. Thus, depending on the delay between drilling and analysis, the internal temperature of the sample might not have stabilized. Because of the uncertainty in the temperature of the samples, we prefer to use the difference between longitudinal and transverse velocities because of the insensitivity of that measure to temperature.

Fig. 2. Theoretical P-wave velocities in the longitudinal (σ = 0) and transverse (σ = π/2) directions as functions of half-angle I.

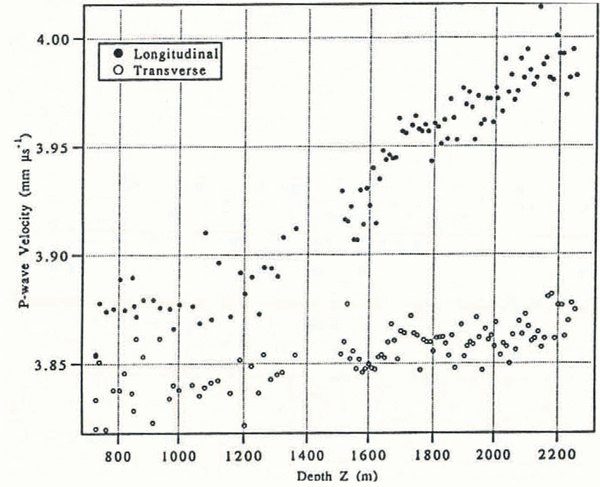
The P-wave velocities in the longitudinal and transverse directions for depths 729-2251 m are displayed in Figure 3. Using measurement errors δl = 0.1 mm and δt = 0.2μs, we calculate δV_P = 0.01 mm μs⁻¹ as the uncertainty in P-wave velocity determination. We convert the velocity difference Δv_p into an average fabric cone angle I by using the theoretical velocity profiles for distributions of c axes (Equation (3) with i = 1).

Fig. 3. Plot of compressional-wave velocity V_p vs depth Z, Longitudinal is for ray paths along the axis of the ice con and transverse is for ray paths perpendicular to the axis Errors for the velocity determinations are ±0.01 mm μs⁻¹.

Figure 4 is a plot of the calculated cone angle I as a function of depth beneath the surface Z. The circles are the individual values of cone angle I, and the heavy line is a 30 m (three-sample) smooth of the data. The solid lines connect individual fabric measurements made by one of us (R.B.A.) on the universal stage using optical birefringence methods. The contour lines delineate the degree circle within which that percentage of c-axes poles are present. For example, the 90% line tells us that 90% of the c axes are within a 60° circle down to a depth of 1600 m but 90% are within a 40° circle at 1700 m.

Fig. 4. Cone half-angle I calculated from P-wave ultra sound vs depth Z. The solid lines are contours that delineate the cone angle that contains that percentage of the crystal axes.

Clearly, the c axes, as measured by the ultrasound, have clustered to within a 50° cone at Z = 700 m and this clustering intensifies with depth. A comparison with the optically determined fabric reveals that the ultrasound measurement of cone angle tracks the 80% cone, i.e. the ultrasound-determined cone angle encompasses 80% of the c axes in the sample. This is not surprising, because the ultrasound method is an “averaging” technique, whereas the optical method counts individual c axes and the presence of a few outliers will expand the 100% cone substantially. The dramatic change in many properties across the Holocene-Wisconsin transition at 1678 m depth (11 640 ± 250 years before AD 1950) in the ice core (Alley and others, 1993; Taylor and others, 1993) is not apparent in the ultrasound-determined cone of c axes. There is a steepening of the gradient at that depth but no step.

The immediate result is that the fabric determined by ultrasound measurements accords well with the traditional optical birefringence (universal-stage) method. At GISP2, we sampled the deep core at 10 m intervals, which is far more frequently than can realistically be done by optical means. The close-order sampling of the ultrasound method can be used as a guide to delineate regions where the optical method reveals more information (e.g. the Holocene-Wisconsin transition). A practical, operational advantage is that it requires only minimal training (< 1 d) to operate the ultrasound equipment but optical measurements require a great deal of time and experience for repeatable results.

3.2. Shear waves

The shear waves produced by the incident Ρ waves at the aluminum-ice interface of the prism-shaped block are qS waves when the measurements are done in the longitudinal direction. This is because the axis of symmetry of the anisotropy is vertical (or near-vertical, since the core has a slight deviation from the vertical) and the plane of the shear-wave particle motions is vertical. The correction for the deviation of the core from the vertical is small because the deviation is small (<5°) and the anisotropy is related to the propagation angle primarily by a cos(σ) term that varies slowly at σ = 0. We therefore use Equation (3) with i = 2 for the shear-wave velocity.

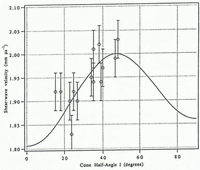
The solid line in Figure 5 is a plot of theoretical qS velocity (Equation (3) with i = 2) as a function of cone half-angle I for σ = 0 (ray path along the symmetry axis). The azimuthal variation in half-angle ΔI is the difference in apparent cone size for shear waves that have particle motions at 90° to each other but the same ray path. Thus, if the horizontal cross-section of the fabric were elliptical, shear waves polarized along the major axis of the ellipse would sense a larger apparent cone angle than shear waves polarized along the minor axis of the ellipse. As a result, the velocities for the two polarizations would differ and the eccentricity of the ellipse can be calculated from the velocity difference Δv_qs = v¹ _qS–v² _qS The velocities vⁱqs are the two orthogonal measurements of longitudinal shear-wave velocity. Clearly, there are multiple solutions for the fabric half-angle I for a given measurement of velocity difference Δ Therefore, we use the half-angle I determined by the P-wave velocity difference Δv_p to constrain the determination of ΔI.

Fig. 5. Shear-wave velocity as a function of half-angle I. Ray path is along the axis of the fabric. The individual points are shear-wave velocities plotted against the cone angle determined by the P-wave analysis. Errors for the velocity determinations are ±0.04 mm μ⁻¹. The six points with I < 30° are from samples in the depth range 1000-1200 m. The four points with 30° < I < 39° are from samples in the depth range 1500-1600 m. The remaining four points (I > 39°) are from samples in the depth range 1800-2200 m.

In Figure 5, we have plotted as open circles the average of the two shear-wave velocities along the ordinate for a selected number of samples (four samples each from the ranges 1000-1200 m, 1500-1600 m and six samples from the range 1800-2200 m). For the abscissa, we have used the cone angle determined for each of those samples by the P-wave method. This is a check on the ability of the shear-wave data to reproduce the cone-angle determination of the P-wave method; perfect reproducibility would cause the point to fall exactly on the smooth curve shown. Some of the variability is due to temperature uncertainty and the remainder is due to the poor SNR of the shear-wave arrivals. Using measurement errors δl = 1.0 mm and δt 1.0 μs, we calculate δV_s = 0.04 mm μ⁻¹ as the uncertainty in qS-wave velocity determination. The higher measurement error in qS-path length compared to P-path length is due to the inaccuracy in placement of the aluminum shear-wave transducer.

The two shear-wave polarizations, while orthogonal, have no true azimuthal (i.e. geographic) reference, because the core has no geographic orientation. Thus, we are not guaranteed that the two polarizations correspond to the major and minor axes of the ellipse. Nor can we ensure that shear-wave polarization measurements on two different samples are in the same (geographic) directions. This difficulty is alleviated by noticing that, for the eccentricities we expect, the radial dimension r of an ellipse is close to the maximum value for a substantial spread of angles around the major axis. Similarly, r is close to its minimum for a large spread of angles around the minor axis. Thus, even for a purely random placement of the transducer, there is a high probability of measuring close to the minimum or close to the maximum, as we now show.

We note that

where x = acos t and y = bsin t with a, b the major and minor axes of the ellipse, respectively, and t the parametric angle. Solving for the range of angles for which r > pa, where p is the percentage of the maximum, we are interested in

(7)

where e = b/a is the eccentricity. For p = 0.9 and e = 0.7, 0 = ±37°. Thus, for more than 80% of our samples (74° range out of a possible 90°), we are assured of measuring a velocity within 90% of the maximum. Since the other polarization is perpendicular, it will have approximately the same probability of measuring the minimum. ^*

Thus, we feel confident that the measured eccentricity e is within 10% of the actual eccentricity in 80% of the cases. Figure 6 is a plot of the inferred cone-angle difference in orthogonal directions vs depth. The error bars are estimated from the size of the cross-correlation peak. The cone is essentially circular at shallow depths and becomes progressively more eccentric deeper. The maximum eccentricity is e ≈ 0.7. The data are sparse and do not allow any conclusions about the effect of the Holocene-Wisconsin transition on fabric. However, it is clear that the drill site has undergone asymmetric vertical compression and transverse extension as would occur during flank flow.

Fig. 6. Azimuthal variation in cone angle (ΔI) as a function of depth. Error bars are estimated from the size of the cross-correlation peak between the orthogonal measurements.

4. Conclusion

We have demonstrated that a commercially available ultrasound unit can be easily learnt and reliably operated to produce repeatable c-axis fabric data. The P-wave measurements accord well with the 80% contour of the birefringence distribution that is the standard way of determining c-axis orientation. The ultrasound measurement can be made more rapidly and often but at the loss of some resolution. The shear-wave data agree with the P-wave results and, in addition, provide inform-ation about the azimuthal variation of the cone angle

We have shown the validity of the technique and now intend to improve the data quality for shear waves and continue measurements on the rest of the GISP2 ice core. If data such as these are collected on more deep ice cores, we can attack problems in ice deformation that have thus far languished due to lack of information about fabrics.