Introduction
During the summers of 1956 and 1957 the University of Torotito sent expeditions to the Salmon Glacier, north-west British Columbia, for the purpose of making various glaciological and geophysical measurements. This paper describes the seismic measurements made during the summer of 1956.
Although the reflection method was used for determining the bottom contours of the glacier (Fig. 6), one refraction spread was made, as well as a seismic velocity study of a thermal bore hole. The latter two studies were useful in determining the seismic compressional wave velocities in the glacier.
The Salmon Glacier is situated in the Coast Ranges just east of the southern tip of Alaska (lat. 56° 10′ N., long. 130° 8′ W.). It flows roughly west to east for a distance of about 10 km., dropping from an elevation of 1,400 m. to 950 m. At this point the glacier divides into two parts, one flowing north into Summit Lake (elevation 826 m.) and the other flowing south to a terminus some 10 km. from the bend, at an elevation of 175 m. Here it is the source for the Salmon River.
The seismic equipment (a portable, 12-channel, shallow reflection, high resolution unit) was flown to a base camp near station S7 (Fig. 6) where preliminary tests were made. These tests indicated the necessity of placing the explosive charge directly into the glacier ice rather than in the snow or firn cover, which was some 6 m. thick at this location. One to two pounds of explosive placed in the ice yielded far better data than as much as ten pounds placed within a meter of the firn–ice interface. To facilitate drilling holes for the charges, which was done with hand tools, the equipment was moved to the lower part of the glacier where the cover was about a meter thick. As the snow melted, the seismic work progressed up the glacier in an attempt to maintain operations on cover of about this thickness. However, a long period of warm weather caused rapid melting of the snow cover while operations at station S6 were being completed; for reasons of safety it was necessary to abandon two proposed geophone spread stations between stations S6 and S7.
Determination of the seismic spread locations and charge locations was done by K. Arnold. Details of the survey methods used, which had to correct for surface movements of some 20 cm. per day, are given by Reference RussellRussell and others (1960) in a paper describing gravity measurements that were made on the glacier at the same time as the seismic measurements.
Seismic Velocity Studies
A single ended refraction profile was made with the shot point at station S9 and the receivers, at 15.25 m. intervals, extending down the glacier for 1,830 m. to station S7. Figure 1 shows two of the recordings obtained, and arrivals of the direct (first arrivals) and the reflected waves are plotted on Figure 2 as a function of distance from the shot point. All charges were placed just into the ice, which at this location was covered by 6 m. of snow, and arrival times were taken as the first downward break in the seismogram traces.

Fig. 1. Typical refraction recordings

Fig. 2. Refraction travel-time results
The first part of the travel-time curve has a slope indicating a velocity of 3,450 m./sec. Because the receivers were on the surface and the explosive charges were at a depth of 6 m., we may interpret the intercept time of 0.007 sec. and the 3,450 m./sec. velocity as indicating a compressional wave velocity of 832 m./sec. in the snow. Thus, the rays traveling along the snow-ice interface refract up to the surface at an angle of about 14° to the vertical, according to Snell’s law. These rays will require 7.5 msec. to reach the surface from the snow-ice interface, so that we can subtract 7.5 msec. from all arrivals and use the snow-ice interface as a datum plane for the following calculations.
Using the usual methods for interpretation of refraction profiles, the travel-time curve on Figure 2 indicates a layer 20 m. thick immediately under the snow-ice interface with a compressional wave velocity of 3,450 m./sec.; this layer lies on top of a layer having a velocity of 3,510 m./sec. The lack of curvature in the travel-time curve beyond 430 m. should indicate the absence of any appreciable increase in velocity for at least some 100 m. below this depth. The nature of the upper layer is not known with certainty. However, the occurrence of many crevasses in this area (as well as over most of the glacier) may well influence the velocity in the upper 20 m. For example, if the crevasses were filled with water (velocity near 1,500 m./sec.) one might expect an average velocity lower than that for solid ice.
The east–west medial section (Fig. 9) shows that the maximum thickness of the glacier between stations S9 and S7 is uniform to within some 30 m. Thus if the reflection arrivals plotted on Figure 2 came from near the deepest part of the glacier and the velocity was nearly constant throughout the thickness, we should expect the reflected travel-time curve to have the form of a hyperbola whose equation is:
where t is the time of arrival at distance x from the explosion, h is the thickness of the glacier, and υ the average compressional wave velocity. The curve drawn through the reflection data points on Figure 2 is the hyperbola that best fits the observed data in the sense of least-squares. Its parameters are:

The close fit of these data to the curve indicates that the above assumptions are not greatly in error. Moreover, as will be discussed more fully later, a thermal bore hole (Granduc No. 5) in this area reached an apparent ice bottom at a depth of 721 m. (Reference MathewsMathews, 1959), which is only four per cent greater than that indicated by the reflection results above.
Reflection Depth Study
The receiver spread contained twelve separate channels, with three receivers (geophones) to each channel. These three geophones were connected electrically in series and were placed 3.66 m. apart along the length of the cable; the center receivers of each group were placed at intervals of 15.2 m. In order to determine the direction from which the reflected waves came, the spread was formed into an L-configuration of 83.8 m. length on each leg. All reflection studies were made with this configuration.
As mentioned earlier, preliminary tests indicated that the charges should be placed into the ice below the snow cover. However, later experiments to test the response when the geophones were also placed below the snow cover yielded poor results. Perhaps the snow cover, along with the numerous crevasses (in many areas constituting half the surface area of the glacier) acts as a very low impedance medium for the seismic energy, that is, the reflection amplitudes appear to be much larger in the snow than in the ice. Thus the snow cover is an ideal place for the receivers. On the other hand, the charge is best placed in the ice, which appears to be a much better transmitter of seismic energy.
Average velocity versus depth was determined from a velocity study in a thermal bore hole (Granduc No. 4) to a depth of 470 m. Figure 3 shows some typical recordings obtained from this study, and Figure 4 is a plot of the average velocity versus depth. For comparison, another such study made by J. R. Weber on the Leduc Glacier (about 8 km. north-west of the Salmon Glacier) to a depth of 366 m. is also shown on Figure 4. These data were obtained from a weighted single geophone, of the type used for the reflection studies, lowered inside an aluminum casing that had been placed in bore hole No. 4 for repeated inclinometer measurements (Reference MathewsMathews, 1959; data from the Leduc Glacier were obtained in an uncased bore hole). Explosive charges were placed at various distances, to a maximum of about 50 m., and at different azimuths from the bore hole.

Fig. 3 Typical bore hole recordings

Fig. 4 Average velocities in thermal bore hole 4, Salmon Glacier, and thermal bore hole 1, North Fork Leduc Glacier
At the time these measurements were made, numerous and very large crevasses which were not filled with water (water in bore hole No. 4 was encountered at 90 m. depth) were observed in the vicinity of the bore hole. It is possible that these crevasses are responsible for the long observed times, and consequently low velocities, for the determinations above 90 m. Although the scatter in these data is rather great, a velocity in the neighborhood of 3,650 m./sec. is indicated. There is also an indication of an increase of velocity with depth; however, this apparent increase may be caused by time delays in the upper 90 m. which would have more effect on the average velocity determinations near 150 m. than on those at greater depths.
On the basis of these compressional wave velocity studies, and for ease in making computations, a constant velocity of 3,660 m./sec. (12,000 ft./sec.) was chosen for the interpretation of the reflection studies, which constitute the major part of the seismic studies made on the Salmon Glacier.
Very few events that could possibly be interpreted as multiple reflections were observed. Moreover, the energy returned to the receivers is in rather discrete time intervals, as can be seen by noting the “log-level” trace on the typical reflection recordings shown on Figure 5. This is the relatively smooth trace which is a time-integral plot of the logarithm of the average amplitude on channel number three. From these facts, one may assume that there is little scattering of energy in the glacier and that the surface absorbs a very large part of the returned energy.

Fig. 5 Typical reflection recordings. (Mixed signals combine energy from adjacent traces)
Several recordings were made at station S1 to test for the best filter settings. Although good reflection arrivals were obtained with a very wide range of filter settings, a sharp low cutoff at 70 c./sec. and sharp high cut off at 140 c./sec. gave the most easily interpreted recordings. Except for a few additional tests at station S7, all the recordings were made with these filter settings. Automatic volume control was used on all recordings.
The L-shaped spread was set up at ten different locations—designated as stations S1 through S10 on Figure 6. The charges were then placed at intervals of 183 m. from the spread in four lines roughly north, south, east and west; these are also indicated on Figure 6. A total of 129 charges were detonated in the lower part of the glacier, which gave 171 reflection arrivals for computation. In the upper part of the glacier 163 reflection arrivals were obtained from 88 charges.

Fig. 6 Contour map of surface and sub-surface topography
The computational procedure used for the interpretation of the reflection arrivals is given in the appendix. Although this procedure is tedious to carry out, it was used because no “datum plane” corrections are needed. The irregular topography, large separations of geophones and shots, and the fact that most of the reflected waves arrived at the surface at large angles to the vertical would make such corrections rather difficult and in many cases inaccurate. The only assumptions required for the computations used here are that all three receivers used for the computation (one at the center and one at each end of the L spread) receive waves reflected from the same plane surface, and that the velocity of the compressional waves throughout the glacier is constant. The first assumption must be made for any interpretation, and the second seems valid from the velocity studies.
The computations were all made on a high-speed digital computer at the Computations Laboratory, Massachusetts Institute of Technology. The computed data (strike, dip, and elevation of the reflection surfaces) were then plotted on a base map. Next, east-west and north-south profiles were constructed every 305 m. by projecting data points, within 153 m. of each profile, to the profile. Reflection points were projected to the profiles along components of dip normal to the profile, and components of the dip in the plane parallel to each profile were plotted on the profile. Smoothed curves were then drawn through these data, care being taken that north–south and east–west curves crossed at the same elevations. In this way, data from adjacent profiles influence the shape of any given profile. Finally, these smoothed profiles were used to construct the bottom contours on Figure 6 and the representative profiles shown on Figures 7, 8 and 9.

Fig. 7 Sections a−a′, b−b′, and c−c′. (Elevation in meters, no vertical exaggeration)

Fig. 8 Sections d−d′, e−e′, and f−f′. (Elevation in meters, no vertical exaggeration)

Fig. 9 East–west and north–south medial sections. (Elevation in meters, no vertical exaggeration)
Except for some thirty “anomalous” reflection events in the upper part of the glacier (to be discussed later), more than 80 per cent of the recorded reflections are from reflecting surfaces within 25 to 30 m. of the smoothed contours. This deviation is in part due to the methods used in projecting reflection points to the profiles; however, most of the deviations are probably due to the difficulty in determining the direction of the reflected wave arrivals.
With the spread lengths used, a misinterpretation of the arrival time, at one end of the spread, of 3 msec. will cause the reflected point to be plotted over 100 m. from its true position.
The solid contour and profile lines on Figures 6, 7, 8 and 9 are based on a sufficient number of reliable data points to yield an interpretation that is thought to be well within the 25–30 m. limits mentioned above. The dashed lines are, in general, based on too few reliable data to make such a statement.
Discussion
In addition to the seismic studies reported here, two other studies, one of a limited extent and one covering much of the area reported here, have been made on the Salmon Glacier to determine its depth. The first of these consists of a line of bore holes drilled by thermal means across the upper part of the glacier (b–b′, Fig. 7) made by the Granduc Mines Limited (see Reference MathewsMathews (1959) for details of the drilling procedures); profile b–b′ (Fig. 7) was drawn along this line of bore holes for comparison with the seismic results. Bore holes 4, 5 and 6 agree very well with the seismically determined depth, but holes 2 and 3 did not reach the depths indicated by the seismic studies. Since it is possible that the thermal heating unit could come to rest on large boulders imbedded in the ice above the bottom, these discrepancies may not indicate that the seismic results have given too great a depth.
The second independent study was by gravimetric means (Reference RussellRussell and others, 1960). Making reasonable assumptions concerning density contrasts, Russell and others calculated depths that agree reasonably well with the seismic data.
In view of these confirmations and the internal consistency of the seismic data, there seems little doubt that the true bottom topography is closely defined by the seismically determined contours.
The general form of the glacier throughout the area studied seems to be approximately that of a V with a depth-to-width ratio of about 1:2. Except for the region near profile c–c′ (Fig. 7), the bottom slopes appear to be extensions of the slopes of the mountains bordering the glacier. Near section c–c′ the apparent width of the glacier determined from the surface shape considerably exceeds the sub-surface width as determined seismically. Moreover, a system of very wide crevasses is developed on the surface near the seismically determined glacier edges.
Another interesting relation between surface and bottom topography exists just north-east of triangulation station fal. Here, a large topographic nose extending north-east of the south-western corner of the “bend” is associated with a large ice fall and large crevasses on the surface. One additional feature of the seismically determined bottom topography should be mentioned, and that concerns the relation to Summit Lake. Reference to the north–south medial profile of the lower part of the glacier (Fig. 9) leaves little doubt that the Salmon Glacier effectively dams Summit Lake.
In the upper part of the glacier between sections a–a′ and b–b′ about thirty rather interesting reflection events were recorded. The reflecting surfaces giving rise to these events strike transverse to the flow direction of the glacier. Moreover, they appear to be vertical near the surface, curving to near tangency with the bottom surface at greater depths. Those reflection surfaces near the east–west medial section are shown on Figure 9; however, the reflecting surfaces extend across a major part of the width of the glacier. Also, as may be noted on Figure 9, the surfaces appear to curve both up and down slope.
Although it may be possible for a large system of crevasses to form reflecting surfaces at shallow depths, the yield strength of ice does not appear to be great enough to support large voids at depths up to 500 m., at least not under the conditions which give rise to surface crevasses. Another source for the seismic discontinuities might be a “layering” of rock debris in the ice. However, one might also expect to find such “layers” in other parts of the glacier, for which there is no evidence.
The shape of these reflecting surfaces, normal to the upper “free” surface of the glacier and tangential to the bottom surface, may indicate some association with stress conditions built up as a result of the ice flow down slope, but how these conditions are manifested as seismic reflections is uncertain.
Acknowledgements
The author is indebted to the following individuals and organizations:
-
The members of the expedition: K. Arnold, along with J. Jacobs, G. Falconer, and F. S. Grant for the survey locations; J. R. Weber and P. J. Hood who worked full time with the seismic equipment, and to R. G. Ostic, L. E. S. Green, and E. B. Freeman for assistance with the seismic measurements.
-
The National Research Council of Canada and the Defence Research Board of Canada who financed the expedition.
-
Granduc Mines Limited who made both surface and air transportation available to the expedition, thus greatly facilitating the operations.
-
The Massachusetts Institute of Technology Computation Center for making available a high-speed digital computer, without which the reflection computations would have been extremely tedious.
Appendix The following treatment is a modification of one developed by Reference RomanRoman (1932) We take the source, S(xs , ys , xs ) and a receiver R i (x i , y i , z i ) (see Fig. 10) at arbitrary positions on the surface of the glacier, which may of course not be a level surface. The first assumption we make is that the energy travels along the straight ray paths SP and PR from the source to the receiver, where p is the point of reflection, i.e. we assume a medium of constant velocity. The energy appears to come from the image point I(x′, y′, z′) so that we may write:
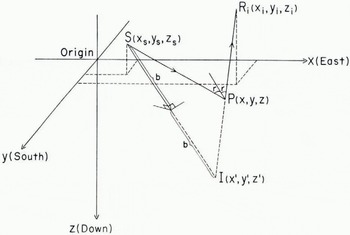
Fig. 10. Construction for data reduction
where v is the velocity and ti is the travel time from s to r along the path SPR, which is the same as that from 1 to r.
The unknowns in this equation are x′, y′, z′ (the coordinates of the image point) and the velocity, v. Thus given four receivers, not all in a straight line, four such equations in the same four unknowns may be obtained, provided that the reflections to the four receivers all come from the same plane surface. This is the second assumption that has to be made. In our case we will take the velocity as known from other measurements and use three receivers for a unique solution for the coordinates of 1.
Letting i = 1, 2, 3 in equation (1), we have the desired three equations, which are quadratic in the unknowns. Subtracting the second of these from the first and the third from the second yields two linear equations in the unknowns x′, y′ and z′. (Subtracting the first from the third does not give a third independent equation.) x′ can be eliminated from these two equations and the resulting equation solved for y′ in terms of z′. Likewise y′ can be eliminated, resulting in an equation between x′ and z′ Substitution for x′ and y′ as functions of z′ from these last two equations in the first of equations (1) yields a quadratic equation in z′ which is easily solved. The positive value of the radical is taken in all cases. With z′ determined, the equations giving x′ and y′ as functions of z′ yield these coordinates.
With the position of the image point, 1, determined we may compute the length of the line SI,
and its direction cosines,
Image theory tells us that the reflecting plane is the perpendicular bisector of this line, so that we may write the equation of the reflecting plane in normal form as:
The line R i I(for example i = 2), whose equations are
intersects the reflecting plane at p, the point of reflection. Simultaneous solution of equations (4) and (5) yields the coordinates of the point of reflection. The dip of the reflecting plane at the point of reflection is given by
and the up-dip direction is
measured clockwise from the positive x (or easterly) direction.












