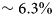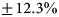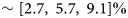Recent and future variability of the ice-sheet catchment of Sermeq Kujalleq (Jakobshavn Isbræ), Greenland

Abstract

Knowledge of ice-sheet catchments is critical for mass-balance assessments, especially glacier-scale input–output budgets. This study explores variations in the catchment of Sermeq Kujalleq, or Jakobshavn Isbrø, Greenland. Six observation-based catchment delineations are evaluated along with a 16-member catchment ensemble calculated from ice-sheet models within the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6). The ‘present-day’ ISMIP6 ensemble mean area was found to be $\sim 6.3\%$ larger than the mean of the observed catchments. Ensemble spreads were comparable in size, $\pm 12.3\%$ and $\pm 15.4\%$, suggesting models are able to delineate the present-day catchment with the same degree of uncertainty as observational methods. The mean catchment area of a 13-member ISMIP6 ensemble shows temporal variation, increasing $\sim [ 2.7,\; \, 5.7,\; \, 9.1] \%$ under three ocean forcing scenarios and a RCP8.5 projection based on one GCM from 2015 to 2100, primarily as the southern catchment boundary migrates southward. This is interpreted as Sermeq Kujalleq exhibiting dynamic piracy, re-directing ice away from adjacent land terminating glaciers. For mass-balance assessments, present-day catchment delineation is more important than capturing the temporal evolution of individual catchments. However, the modeled temporal changes in catchment area are potentially underestimated, as the models exhibit insufficient acceleration of inland ice flow.

1. Introduction

1.1. Temporal catchment variability and ice-sheet mass balance

Given the Greenland Ice Sheet's (GIS) potential to both respond to climate and affect sea-level, previous, current and future changes in the mass balance of the ice sheet are being assessed with both observations and models (e.g. Shepherd and others, 2012; Larour and others, 2017; Moon and others, 2020; Goelzer and others, 2020; IMBIE, 2020; Mankoff and others, 2021). After decades of relative stability, the ice sheet started to lose mass at an accelerating rate in ~1998 in response to warming ocean and air temperatures (Khan and others, 2015; Mouginot and others, 2019; IMBIE, 2020).

The mass balance of the GIS is the difference between mass gain through accumulation of snow and mass loss through meltwater runoff and frontal ablation (the sum of iceberg calving and submarine melt) (Cuffey and Paterson, 2010). Fully capturing the change in each of these major mass-balance components is difficult (e.g. Mankoff and others, 2020a, 2020b; Karlsson and others, 2021), leading to vastly different mass-balance estimates (Rignot and others, 2011; Shepherd and others, 2012). Mass balance is often described in terms of the balance between surface mass balance (SMB) and ice dynamic loss (e.g. van den Broeke and others, 2009; Khan and others, 2015; Kjeldsen and others, 2015).

Three different observational methods are used to estimate the mass balance of the GIS (Khan and others, 2015): (1) gravimetry, where changes in the Earth's gravity field due to changes in ice mass are observed (e.g. Luthcke and others, 2006; Velicogna and others, 2014), (2) satellite altimetry, observing changes in the surface elevation of the ice (e.g. Zwally and others, 2011; Khan and others, 2022) and (3) the input–output method, which combines satellite observations of ice flow velocities with SMB models (e.g. Mouginot and others, 2019; Colgan and others, 2019).

The GIS is comprised of hundreds of individual outlet glaciers, both marine and land terminating, that respond differently to climate change. It is therefore important to understand the response of these individual glaciers, in order to understand the sea-level contribution of the greater ice sheet. Drainage basins, also called catchments, are used to study the mass balance of individual glaciers (e.g. Rignot and Kanagaratnam, 2006; Howat and others, 2011; Rignot and others, 2011; Mouginot and others, 2015) or conglomerates of glaciers (e.g. Colgan and others, 2019; Mouginot and others, 2019). Drainage basins refer to the upstream area that is being drained by a single glacier. Glacier-scale mass-balance studies allow us to gain an understanding of the processes controlling changes of individual glaciers. Such studies, however, may introduce additional uncertainty in mass-balance estimates if the catchment is not accurately captured. While uncertainties in the grounding line flux estimates depend on uncertainties in surface velocities, ice thickness and how surface velocities relate to vertically averaged velocities, SMB uncertainties come from the SMB model and the area over which the SMB is integrated. The relative importance of these uncertainty contributions can vary significantly for different glaciers. It can be difficult to identify the consequence of any one contributor to the mass budget of a single glacier catchment (Mankoff and others, 2020b). Consequently, basin-scale mass-balance studies are sensitive to the method being used to delineate the catchment area over which the SMB is being integrated and then compared to the discharge through the grounding line (van den Broeke and others, 2009). Frequently, observation-based catchments are assumed to be temporally invariant, which can impact studies of basin-wide mass balance on longer, centennial timescales (e.g. Kjeldsen and others, 2015; Khan and others, 2020; Box and others, 2022). Of the commonly used methods to estimate glacier-scale mass change, the input–output method is perhaps the most sensitive to delineation of drainage basins, as basin uncertainty asymmetrically influences area-integrated SMB input and not cross-sectional ice discharge. With the input–output method, an area-integrated SMB, which is dependent on catchment delineation, is subtracted from grounding line discharge. Calculating area-integrated SMB for difference against grounding line discharge makes uncertainty in SMB directly proportional to uncertainty in catchment area. A concrete example of this is given in section 1.2.

This study aims to evaluate the potential for temporal variability in catchment areas and the impact this might have on basin-wide mass-balance estimates. Sermeq Kujalleq, also known as Jakobshavn Isbrø, is one of the largest and most dynamic glaciers in Greenland (e.g Lemos and others, 2018; Mankoff and others, 2020b). In recent decades, it has thinned, accelerated and retreated significantly (e.g Holland and others, 2008; Joughin and others, 2008). These changes, focused at the terminus, could be expected to translate into changes in the inland catchment area. As such, Sermeq Kujalleq provides a useful setting for investigating a potentially changing catchment area. Additionally, field observations already suggest an ongoing shift in flow direction (i.e. azimuth) along the northern boundary of the Sermeq Kujalleq catchment, more than 100 km inland from the calving front, which is a strong indication of a temporally variable catchment (Lükkegaard and others, 2024). The findings of this study are expected to be representative of other areas of the GIS, consequently drawing conclusions on catchment evolution in general.

Although the amount of available satellite data has increased dramatically in recent years, studying the temporal evolution of catchments from satellite-derived velocity maps is not yet feasible. The majority of the GIS ice flow is slow-moving, consequently, limitations in both spatial and temporal coverage of satellite-derived velocity maps prohibit the possibility of exploring the decadal-scale temporal evolution of observation-based catchments. For example, for Sermeq Kujalleq there is only sufficient catchment-wide satellite velocity data available starting in the last 10 years (Joughin and others, 2010), and altimetry data starting in the last 20 years (Zwally and others, 2005). A catchment delineation tool was therefore designed to work specifically using ISMIP6 convention modeled surface velocity products, producing simulation-based catchments over longer time scales. Here, we use simulated velocities from an ensemble of 16 different models from the ice-sheet model intercomparison project (ISMIP6) (Nowicki and others, 2016). ISMIP6 was chosen because it is the most comprehensive inter-model comparison exercise. Using several models allows us to minimize the catchment changes associated with model drift. Model drift is the unintended, gradual accumulation of errors or biases in a simulation resulting in the deviation of a model state from its expected conditions over time. Before exploring temporal catchment changes, it is essential to establish how well the community state-of-the-art ice-sheet models are able to capture the observed present-day Sermeq Kujalleq catchment.

1.2. Observation-based ice-sheet catchment products

Glacier catchments are commonly delineated using either ice surface elevation or surface velocities. More recent catchment products are using a combination of both methods. Generally, elevation delineations follow the steepest surface elevation slope while velocity delineations follow a given ice-flow streamline. Below, each presently available catchment product is presented, and we hereafter refer to it by the name of the first author.

One of the first publicly available, and still very commonly used, catchment boundary products is the Zwally basins. The original Zwally basins were first made available in 2001, delineated from ERS altimetry (Zwally and Giovinetto, 2001). They were since updated when new ERS-1 and 2 products became available (Zwally and others, 2005). They were updated again using ICESat altimetry covering the period 2003–2005 (Zwally and others, 2011). This is the catchment product used for the Ice-Sheet Mass Balance Inter-comparison Exercise (IMBIE, 2020). Zwally basins were delineated according to maximum down-slope gradient of the surface Digital Elevation Models (DEM), but a detailed and fully traceable description of how these catchments were delineated is not available, for example, detailing the degree of ice-surface smoothing.

The Krieger individual glacier drainage basins (Krieger and others, 2020) were delineated using a combination of observed surface velocity and an ice surface DEM since the assumption that ice flows downhill along the maximum ice surface gradient does not always hold true for areas of fast ice flow. The combination was done by adapting a watershed method in such a way that DEM surface slope was disregarded in areas of fast moving ice, where the velocity exceeded some predefined threshold (chosen to be 13.67 m a⁻¹ based on which velocity value resulted in the maximum angular correlation). The DEM from which the catchments are delineated was smoothed by a kernel with a width 20 times the local ice thickness. Krieger and others (2020) performed a detailed sensitivity study, testing the catchment area sensitivity to different choice of input velocity and DEM data products, the impact of smoothing the DEM and the effect of introducing Gaussian noise in the datasets. The study found a notable impact on catchment area from different choice of DEM and ice velocity data and that using both ice velocity and DEM data produced more consistent catchments compared to only using a DEM. This product used TanDEM-X elevations and Sentinel-1 velocity measurements, with temporal coverage of 2011–2014 and 2014–2019, respectively.

The Mouginot catchments (Mouginot and others, 2019) were delineated in a similar fashion to the Krieger product. However, a specific description of choices, such as the seed region and method for selecting velocity limit, and smoothing, has not been made publicly available. This product used a composite velocity map (Mouginot and others, 2017) above threshold velocity of 100 m a⁻¹ and surface slopes from GIMP DEM (Howat and others, 2014) smoothed over ten ice thicknesses, with temporal coverage of 1992–2016 and 2009–2015, respectively.

The Mankoff catchments were delineated using a watershed algorithm (Mankoff and others, 2020a) and applying it to the surface defined by the hydraulic head, rather than the ice surface elevation. The hydraulic head is defined as $h = z_{\rm b} + k{\rho _{\rm i}\over \rho _{\rm w}}( z_{\rm s}-z_{\rm b})$. Here, z _b is the bed elevation, z _s is the ice surface elevation, ρ _i is the density of ice (917 kg m⁻³), ρ _w is the density of water (1000 kg m⁻³) and k is the flotation fraction. The flotation fraction represents the ratio of water pressure to the overburden pressure exerted by the ice, where differing values represent variation in effective basal pressure regimes which affects sliding. The study explores the sensitivity of the catchments to different choices of k. In case k = 1 means high subglacial water pressure where flotation is reached. In case k < 1 the subglacial water pressure is reduced lowering the potential for sliding. This method eliminates the need for a seed region. The Mankoff product used ArcticDEM v7 for surface elevation (Porter and others, 2018), and Bedmachine v3 for bed elevation (Morlighem and others, 2017).

Other studies (e.g. Bindschadler, 1984; Rignot and Kanagaratnam, 2006; Lewis and Smith, 2009) have delineated catchments, but without explaining the procedure for doing so, or making the catchment outlines publicly available. The Krieger and Mankoff products are both well documented and have re-traceable methods. The Sermeq Kujalleq catchment for each of the four publicly available catchment products is shown in Figure 1. The Mankoff catchment shown here used k=1. Drainage sector 7.1 from the most recent Zwally product is taken as the Sermeq Kujalleq catchment. The Krieger catchment is the combination of two drainage basins from the Krieger catchment product, merged into one. This was done to allow a direct comparison with the other products.

Figure 1. Overview of four available delineated Sermeq Kujalleq catchments; Zwally product (Zwally and Giovinetto, 2001), Krieger product (Krieger and Floricioiu, 2021), Mouginot product (Mouginot and others, 2019) and Mankoff product (Mankoff and others, 2020a). Map coordinates are given in projection frame EPSG: 3413 with units of kilometers. They are plotted on top of ArcticDEM (Porter and others, 2018) relief and velocity map with the use of QGreenland (Moon and others, 2021).

The catchment area for all four products is calculated as a 2D surface, i.e. not taking vertical variation into account. These catchments are all fairly similar in the shape of their outline, but do have noticeable differences in area, ranging in size from the smallest (74483 km² Mankoff's) to the largest (95458 km² Zwally's). The discrepancy between catchment areas, due to both difference in delineation methods and also the choice of input observation, will influence the area over which SMB variables are being integrated for input–output assessments. Common to all four catchment products is that they are assumed to be temporally invariant.

Although not shown in Figure 1, Rignot and Kanagaratnam (2006) find the area of the Sermeq Kujalleq catchment to be 92 080 km². Bindschadler (1984) finds an upper and a lower estimate of the Sermeq Kujalleq catchment area intended to bracket the actual catchment, we therefore use their mean of 80 750 km². Both estimates are within the range of the four shown catchments. When referring to the mean of the observed catchments throughout this manuscript, it is based on all six mentioned catchment areas. The mean area of the six catchments is 84 430 km². Of the six catchments, the smallest delineated Sermeq Kujalleq catchment (Mankoff) is ~11.8% smaller than the mean observed catchment area. The largest delineated Sermeq Kujalleq catchment (Zwally) product is ~13.1% larger than the mean observed catchment area. Table 1 shows a full overview of absolute and relative areas for each individual observation-based catchment product.

Table 1. Overview of previously calculated catchment areas, given both as absolute area in km² and in percentage relative to the mean area

If you integrate the reference RACMO SMB product in QGreenland over the four observed Sermeq Kujalleq catchments shown in Figure 1, the resulting area-integrated SMB input ranges from 24.8 Gt a⁻¹ with the Mankoff catchment to 31.8 Gt a⁻¹ with the Zwally catchment (Moon and others, 2021). This spread of 7.0 Gt a⁻¹ represents a ±12.6% uncertainty in SMB input to Sermeq Kujalleq's catchment depending on choice of catchment. This highlights how uncertainty in catchment SMB input is directly proportional to uncertainty in catchment area.

2. Method

2.1. Delineation tool

To evaluate the temporal evolution of the simulation-based catchment area, a simple delineation tool was created in Matlab (R2021a) software. This tool takes surface velocity maps as input, and outputs a polygon estimating the Sermeq Kujalleq catchment. The delineation process is initiated by calculating flowlines starting at points near the outlet of Sermeq Kujalleq. The northern and southern catchment boundaries are then defined as the flowlines containing the minimum and maximum y-coordinates interpolated at some chosen x-coordinate, x _outer. The catchment is closed by a streamline starting at the end point of the southern catchment boundary and ending at the end point of the northern catchment boundary. Figure 2a shows an example of these described steps. This approach means the locations where flowlines start influence the final delineated catchment. We define a ‘bounding box’ encompassing both land and ocean terminating ice, where we search for points to start flowlines from. Note, Krieger and others (2020) refer to the bounding box and the specific points where flowlines are started from as ‘seed region’ and ‘seed points’ respectively. Within the bounding box, a flowline is started from any grid point where the model output velocity magnitude is larger than some arbitrary limit, v _lim. Each flowline is calculated using trigonometry from the easting and northing input velocity components. The delineation tool also provides the number of points making up a flowline (n _p), and the distance between each point in the flowline (d). The tool can produce three different ‘types’ of flowlines (1) reverse flowlines going in the upstream direction of flow, (2) forward flowlines moving in the downstream direction of flow, and (3) flowlines going in both directions from the given starting point. This study uses the reverse option. A reverse flowline is stopped when reaching an upstream velocity slower than 0.5 m a⁻¹.

Figure 2. (a) Example of the delineation tool applied to an UAF PISM1 exp05 velocity map. Black rectangle indicates the bounding box area, black points within bounding box show gridpoints from which (gray) flowlines are started. Thick white lines denote the outermost streamlines defining the catchment, using x _outer = −150 km (black dotted line). The magenta flowline closes the catchment. (b) Close up of bounding box. Grid points within the bounding box are highlighted with either a dot – where no flowlines are started – or a colored circle with a number indicating the total number of flowlines started from that gridpoint across all timesteps in the projection run. This showcases the front retreat occurring in this simulation. The white lines indicate the 2015 and 2100 delineated catchment boundary.

We tested the sensitivity of the catchment area to the choice of v _lim, x _outer and the corner points of the bounding box. The delineated catchment was found to be highly sensitive to the choice of bounding box and v _lim, with poor choices in values resulting in more frequent large year-on-year changes in catchment area (i.e. step-wise changes). A more detailed description of this sensitivity study can be found in Supplementary S1. Ultimately, v _lim = 10 m a⁻¹ was found to produce the most robust delineated catchments for simulations representing both present-day conditions and projections. The choice of location of the bounding box at the front of Sermeq Kujalleq had a relatively big influence on the final delineated catchment. This is especially true for transient model runs, since the bounding box needs to encompass the entire outlet region over the full time period of a given model run, taking into account the potential retreat over time. We explored an arbitrary range of bounding boxes. The corner points of the bounding box were then set to x _min = −223 km, x _max = −150 km, y _min = −2295 km, y _max = −2240 km, in north polar stereographic projection coordinates (EPSG: 3413), to produce the smallest year-on-year variation in area over time.

It was found necessary to decrease the bounding box area for the LSCE GRISLI model run in the easting direction from x _min = −223 km to x _min = −181 km (Supplementary S1). The delineated catchment is not very sensitive to the choice of x-coordinate at which the outer flowlines are determined. Therefore x _outer = −150 km was chosen arbitrarily and kept constant for all ensemble members and time slices. The flowline parameters were chosen as n _p = 550 and d = 1000 m. This tool was applied to simulated velocity fields from (1) the final time step of the ISMIP6 historical run and (2) all annual timeslices from three ISMIP6 projection runs forced by different ocean forcing scenarios from a single Global Climate Model.

2.2. Modeled surface velocity maps

ISMIP6 aimed to reduce the uncertainty in the future ice-sheet contribution to sea-level change related to individual models and modeling choices. This was done by carefully designing experiments, in support of the Climate Model Intercomparison Project (CMIP6), and encouraging many different ice-flow models to do these standardized experiments. A more detailed explanation of the ISMIP6 design and protocol can be found in Nowicki and others (2016, 2020) and Goelzer and others (2020). Here, we will briefly describe the chosen experiments for which the catchment of Sermeq Kujalleq was delineated.

Projection runs start in 2015 and end in 2100, with models initialized to fit the ice-sheet state at the end of 2014 to the best of their ability. Participating groups submitted a ‘historical’ run, which brings the various model spin up states to the common January 2015 starting point for projection runs. This was needed because the models used differing approaches when initializing the ice sheet. These include long interglacial spin up, data assimilation of present-day observations or some combination of the two (Goelzer and others, 2018).

In the case of paleo-climate spin ups, the model is run forward in time for tens to hundreds of thousands of years, while forced with reconstructed or modeled climate boundary conditions (e.g. Aschwanden and others, 2013; Greve, 2019). The advantage of this method is that anytime during the simulation the state of the model is consistently responding to the applied forcings. This means that factors such as limited spatial resolution and uncertainties in climatic boundary conditions can result in considerable deviation between the initialized state and the present-day observations (Goelzer and others, 2018). This deviation can be alleviated through the use of constrained, or nudged, spin ups, whereby simulated ice-sheet thickness and/or velocity are forced to reproduce observational datasets through mass and/or flux adjustment terms between time steps. Virtually all ISMIP6 members use such constrained spin ups, on at least centennial scales, rather than unconstrained, or transient, spin ups, in which simulated ice thickness and velocity can significantly deviate from reality.

Data assimilation methods, on the other hand, make use of geometry and ice-flow observations to create an initialized present-day ice-sheet state, by inverting for unknown basal conditions (e.g. Rückamp and others, 2020). The data assimilation initialized states are consequently constrained through inversion to observations. They therefore capture the present-day geometry well. However, the inferred basal parameters only match present-day conditions, and cannot evolve forward in time (Goelzer and others, 2018). This initialization method can also result in an imbalance between the external forcing and the ice flux, causing a model drift unrelated to climate (Seroussi and others, 2013). Also, this method does not accurately capture the thermodynamic state of the ice sheet. Therefore, some models choose to re-calculate the thermal state with a paleo-simulation, which will then have a different geometry, that is interpolated to match the geometry from the data assimilation initialized state. Because each model uses a different initialization procedure, the time period covered in each historical simulation will vary (Nowicki and others, 2020). We only look at the last time step of each historical simulation approximating the true ice-sheet state at the end of 2014.

Additionally, to the historical experiment, we explore three different ISMIP6 experiments. Experiment05, hereafter exp05, was selected for analysis as it performs well over Greenland (Barthel and others, 2020). It is forced using the high emission scenario, Representative Concentration Pathway (RCP) 8.5 (Van Vuuren and others, 2011), using climate forcing fields from the atmosphere-ocean general circulation model (AOGCM) MIROC5, and with ‘medium’ values for the parameters in the submarine melt rate parameterization. The two other experiments differ only in the applied ocean forcing, exp09 (high ocean forcing) exp10 (low ocean forcing).

The associated projection control run was also included in this study. The run spans the same time range as the projection run, but without a transient climate or oceanic forcing applied; instead steady-state atmospheric and oceanic forcing is applied. The control run therefore provides an indication of model drift which can arise from, e.g numerical errors, inaccurate initialization or simplified dynamics of ice flow. The difference between the experiment and control runs is the transient response to transient climate and ocean forcing.

Of the 13 groups participating in ISMIP6, ten supplied files containing the necessary surface velocity variables needed by our delineation tool for the chosen ISMIP6 runs (Goelzer and others, 2020). These included models using both finite difference (FD) and finite element (FE) methods, and additionally, each individual model is free to use different grid resolutions. However, for the purpose of comparison, the native resolution of each model run was subsequently re-gridded to a common 5 km grid by the ISMIP6 group before being made publicly available. Also, some of the participating groups provided more than one simulation for a given experiment, but using a different set of parameter values. Following the definition from Goelzer and others (2020), each of these simulations is regarded as an individual ‘model’, even though the ice-sheet model used for the simulations is the same. This is done since modeling decisions can be more important for the results than the underlying numerical scheme. The total number of available simulations for this study is therefore 16. See Table 2 for an overview of these models.

Table 2. Overview of the ISMIP6 simulations used in this study

Listed for each model is the numerical scheme (NS), FE: finite element, FD: finite difference, the stress balance (SB), HO: higher order, HYB: hybrid of SIA and SSA, the initialization method (IM), DAv, DAs, DAi: data assimilation of velocity, surface elevation and ice thickness respectively, SP: spin-up, CYC: transient glacial cycle(s), NDs: nudging to surface elevation. Model characteristics described here follows Table A1 from Goelzer and others (2020). Also listed is the public availability of the experiments of interest, H: historical, C: projection control run, Exp: ISMIP6 experiment 5 (exp05), 9 (exp09) and 10 (exp10).

3. Results

3.1. Catchment variation of final time-step of historical simulations

We compare modeled catchments against observed catchments to explore differences in the mean areas of both ensembles. We use the historical simulations as described in the method section for this. The model runs show variation in ice flow velocity, ice front extent and overall ice geometry. This variation between the modeled ice-sheet states stems from the different initialization methods and parameter choices used by the groups.

Figure 3 shows all 16 simulation-based delineated catchments, plotted as normalized binary masks to show agreement in catchment location between models. The historical simulation ensemble mean area is 89 739 km², making it ~6.3% larger than the observation-based catchment mean. The largest catchment was derived from the JPL ISSM model output, with an area $\sim 18.3\%$ larger than the mean area of all models. The smallest area is $\sim 34.6\%$ smaller than the model ensemble mean area from the LSCE GRISLI model, see Table 3. The GRISLI run is considered an outlier, since its calculated catchment area is more than 3 standard deviations (SD: $\pm 11.2\%$) away from the mean. Aside from JPL ISSM and JPL ISSMPALEO, the remaining 13 models are in close agreement, both in regards to extent and area size. Their variation in area from the mean is around the same order of magnitude as that of the observed catchments.

Figure 3. Common catchment area mask of the ensemble of models, for the final time step of the historical run (i.e. 2015). The color indicates the agreement between models, calculated by taking the sum of a binary mask and normalizing to the maximum number. If 16, all models agree that the point is located within the catchment. The closer to 1, the less the models agree.

Table 3. Overview of calculated catchment areas from ISMIP6 historical simulations, given both as absolute area, A, in km², in percentage relative to the ensemble mean area, ${\bar A}_{\rm E}$, and in percentage relative to the observed mean area, ${\bar A}_{\rm O}$

The ensemble spread gives an indication of the accuracy with which the models are able to capture the observed catchment. The ensemble spread of historical simulations is $\sim 26\%$, however, excluding the GRISLI simulation reduces the ensemble spread to $\sim 15.4\%$. This is almost the same as the ensemble spread of the five observed catchment areas, which is $\sim 12.3\%$. This means that, although the ISMIP6 simulations were designed to evaluate uncertainty between ice-sheet models rather than catchment-scale dynamic studies, ISMIP6 ensemble members can reproduce a similar range of present-day catchments that reflect observations. As these historical simulations have been constrained in various ways to represent present-day state, this time slice reflects when the delineated modeled catchment will be most similar to observed catchments. Delineated catchments under transient projection runs (exp05, exp09, exp10) are expected to deviate more from observations.

3.2. Catchment evolution of projection runs

Not all of the model runs used to evaluate the catchment of the historical runs were also available when analyzing the modeled projection runs (exp05, exp09, exp10). Only 13 models were available for evaluating the relative change in catchment area over time. See Table 2 for an overview of the models. The delineated catchment for the years 2015 and 2100 for each model can be seen plotted on top of the modeled 2015 ice flow velocities in Figure 4.

Figure 4. Delineated catchment for the first and final time step for 13 models following exp05 conditions, plotted on top of the modeled 2015 surface velocity (m a⁻¹) of each model. The area to the left of the vertical dotted line (x _p = −100 km) is not included in the catchment area calculation.

When calculating the area of Sermeq Kujalleq's simulation-based catchment, everything west of x _p = −100 km is not included as part of the catchment area. This frontal region is where the largest artificial deviations in area due to sensitivity to seed points were found. Excluding this region generally cleans the area curves of unrealistic fluctuations associated with sensitivity to changes within the bounding box to get overall clearer signal. This allows focus on the far inland changes in the catchment, without the influence of the expected front retreat. Supplementary Fig. S3 shows an example comparison of the relative change in area including and excluding the front for one model output. As was seen in the analysis of the historical model runs, the LSCE GRISLI model run showed by far the smallest catchment area. This continued for the transient run and, additionally, it was the only model which showed decreasing catchment area between the end and start of the simulation for all three experiments, see Figure 5. Otherwise, the majority of the other models generally agree on an increasing catchment area over time. The LSCE GRISLI run was therefore excluded when calculating ensemble mean area. The ensemble mean area of the final time step was found to be [87 100, 89 992, 84 654] km² for exp05, exp09 and exp10 respectively. Meaning, the ensemble mean area increases by [5.7, 9.1, 2.7]% between 2015 and 2100.

Figure 5. Relative change in catchment area of the 13 models from 2015 to 2100 for exp05 (blue), exp10 (yellow) and exp09 (red). Note, the LSCE GRISLI run of opposite sign was excluded when calculating the mean and standard deviation.

As suspected, higher ocean forcing results in enhanced temporal variability of the simulation-based catchments. Supplementary Figure S4 shows the temporal catchment area change before it was cleaned from step-wise changes.

The temporal change in y-coordinate of the southern and northern simulation-based catchment boundary at projection coordinate x _p = −100 km is shown in Figure 6 for exp05. We find an asymmetric trend in the northern and southern boundaries, as both margins of the catchment are moving in opposite directions and at different magnitudes. The models generally show the largest shift of the y-coordinate along the southern boundary, mainly moving further south over time. We find a maximum southward y-coordinate migration of ~10 km between 2015 and 2100 for model run GSFC ISSM. The northern boundary generally also agrees on moving more northward over time, with a maximum change of ~5 km for the three AWI ISSM model runs. Supplementary Figure S5 shows the boundary migration for the three examined ISMIP6 experiments. This supplementary figure includes step-wise changes in the y-coordinate related to sensitivity to the delineation tool which was cleaned from Figure 6. Boundary migration of exp09 and exp10 show the same general trend as exp05.

Figure 6. Change in the y-coordinate from the first time step, of the (a) southern and (b) northern delineated catchment boundary at x _p = −100 km, color coded according to the given model. The Greenland insert shows the position where the temporal boundary migration is examined.

4. Discussion

4.1. Variation in observed catchments

Variation in catchment delineation presents a non-trivial issue for catchment-scale input–output SMB studies. If an individual glacier catchment is defined as either too large or small, the catchment-wide SMB estimate will be correspondingly biased high or low. Existing observation-based delineations do not presently agree on the actual catchment of Sermeq Kujalleq. The six observationally delineated products show an ensemble spread $\pm 12\%$. This discrepancy is not only due to the difference in delineation methods used. The Mouginot and Krieger products use a very similar method, however, different choices of seed region, velocity input and limit, and surface DEM have resulted in a difference in area between the two products of $\sim 8.8\%$. Through sensitivity testing, Krieger and others (2020) found a significant discrepancy of up to 16% in catchment areas using the same method but different sets of surface DEM and velocity maps.

As described in the introduction, the SMB uncertainties come from the SMB model and the area over which the SMB is integrated. Fettweis and others (2020) compared modeled ice-sheet-wide SMB estimates from 13 regional climate models and evaluated them against a range of observations for the period 1980–2012. Based on this study, it appears that relative uncertainty in modeled SMB ($\pm 22\%$). This is larger than the observation-based catchment ensemble spread of $\pm 12\%$. However, the spread in the ISMIP6 modeled catchments is still significant, meaning that although it will be difficult to figure out the true/best representative catchment, a consistent boundary product will reduce catchment-scale SMB biases presently associated with inconsistent delineations of catchment boundary.

Aggregating adjacent catchments results in lower uncertainty in the SMB for the conglomerate, as uncertainty related to catchment boundary position is minimized due to spatially compensating errors between adjoining catchments. Geometrically, the length of the individual GIS glacier catchment boundaries along the margin of the ice sheet is typically significantly shorter than the inland boundaries. When aggregating catchments, this difference in lengths becomes smaller and smaller, meaning that for conglomerates and catchment-wide SMB estimates the choice of ice mask becomes even more significant. Due to the elongated shape of the GIS, deviations in the ice mask can result in large variation in regional mass-balance estimates. Similar to this study, exploring of the effect of inherently assuming temporally invariant catchment boundaries Kjeldsen and others (2020) highlights that ice masks used in mass-balance studies are static in time, and that ice mask products have timestamps spanning more than a decade, and vary in resolution, depending on the imagery from which they were created. That study suggests that mass-balance studies should start using standardized dynamic, fine-resolution ice masks that are periodically updated to match recent changes in ice extent.

Even though many SMB studies use aggregated catchment basins, individual basin boundaries are still needed. As more data with high spatial resolution become available, more studies examining the dynamic evolution of individual glaciers are being conducted (e.g. Vijay and others, 2019; Moon and others, 2020). Therefore, a common nested catchment product seems most helpful, this way users could select the level of catchment aggregation needed for a given study. Presently, there is an open science effort to make scientific results reproducible. This is important if we want to develop standardized catchment products, allowing the method of delineation, the choice of input observations and time coverage to be agreed upon.

Preceding delineation studies have revealed critical information that should be considered when working toward a common nested catchment product. Krieger and others (2020) highlight the importance of including velocity information when delineating drainage basins by comparing delineated catchments at Nioghalvfjerdsfjorden and Zachariae Isstrøm using a modified watershed method (using both ice surface DEM and velocity maps) and the classical watershed method (applied to only an ice surface DEM) and found a region of significant size (20 km wide) potentially miss-classified when using the classical method. When using velocity information to delineating catchments, the size of present-day catchments is highly dependent on the choice of seed region. This is clear when assessing the catchment products of Mouginot, Krieger and this study. Although Mouginot and Krieger use similar delineation methods, they choose different numbers of seed regions such that the full Greenland catchment products vary in the number of catchments. Mouginot divides the GIS into 260 catchments and aggregate them into seven sectors. Out of the 260 glaciers, 217 are marine terminating and 43 are land terminating. They note that the actual number of land-terminating glaciers in Greenland is far greater than 43, but they have been lumped together for simplicity. Krieger delineated 328 major outlet glaciers. This discrepancy in the number of outlet glaciers will clearly affect individual delineated catchments. Simply put, the SMB uncertainty associated with catchment choice is only completely eliminated when estimating SMB for the entire GIS. The smaller the catchment, the larger the relative uncertainty in catchment-scale SMB becomes.

4.2. Comparison with observations

4.2.1. Comparison with satellite data

To evaluate the trend in simulated catchment area over time, we calculate and compare observation- and simulation-based accelerations of ice flow for a region near the front of Sermeq Kujalleq. Observed accelerations were calculated from two PROMICE winter velocity maps from 2017 and 2021 (Solgaard and Kusk, 2022).

Figure 7 shows the difference between observed and simulated ice flow accelerations for 2017–2021 within the delineated catchment area and below the 2000 m elevation line. The models show the same general spatial pattern of significantly underestimating ice flow acceleration in the fast-flowing frontal part of Sermeq Kujalleq, then immediately upstream of this overestimating ice flow accelerations. The models are then again underestimating the acceleration in the slower moving inland section. These observation- and simulation-based accelerations were plotted against one another and a linear fit was generated for each individual model. Supplementary Figure S6 shows a sample plot of the linear fit. The fit parameters for each model can be found in Table 4. Even though all models exhibit areas where acceleration is overestimated, all with the exception of the LSCE GRISLI run show a net negative bias. It is therefore concluded that the models tend to underestimate observed ice flow acceleration between 2017 and 2021.

Figure 7. Ensemble difference in acceleration (a _model − a _observed) in (m a⁻¹) from 2017 to 2021, constrained within the modeled catchment area and below the 2000 m elevation line (Morlighem and others, 2017). Observed accelerations were calculated from satellite-derived winter velocity maps with temporal coverage (12 January–15 February 2017 and 13 January–06 February 2021) (Solgaard and Kusk, 2022). Black points show in situ survey sites.

Table 4. Fit parameters of observed vs modeled acceleration from 2017–2021 scatter plots

Here, r is the coefficient of determination, bias is the difference between the mean modeled and observed accelerations, RMSE is the root-mean-square-error and N the number of points evaluated.

Studies have shown that capturing the high velocities of ice streams in ice flow simulations remain challenging (Fox-Kemper and others, 2021). This underestimation of velocities is related to difficulties in fully capturing a number of complex processes. For instance, some model studies have found that additional heating mechanisms such as cryo-hydrological warming, which causes softening of the ice, are required to capture high flow speed (Phillips and others, 2010; Lüthi and others, 2015). Depending on the type of initialization method, changes in the thermal state of the GIS have been suggested to either insignificantly (Seroussi and others, 2013) or significantly (Zhang and others, 2024) affect ice-flow simulations. Furthermore, in both cases these thermal states do not capture recent secular increases in englacial temperatures associated with recent climate change. It would be helpful to have the ISMIP6 3D thermal states made publicly available when evaluating the evolution of the simulation-based catchment boundaries.

Ice-ocean feedback mechanisms are also difficult to capture and these have a big influence on the velocity of marine-terminating glaciers such as Sermeq Kujalleq. Sermeq Kujalleq especially has a history of rapid change in velocity (Joughin and others, 2004, 2008). However, even though simulated accelerations are underestimated, simulated inland ice flow is still speeding up over time in the high-emission scenarios as expected. The ice discharge across the grounding line is related to catchment area. This means that an increase in catchment area can result in an increase in ice discharge, and vice versa. Isolating temporal trends in discharge and catchment area therefore becomes important.

4.2.2. Comparison with in situ data

To evaluate the trend in simulated catchment area over time, we examine the few available in situ observations of surface velocity and azimuth within Sermeq Kujalleq catchment. Unfortunately, these are located near the northern catchment boundary, where the ISMIP6 ensemble suggests there is less temporal variability in catchment area. The trend in simulated velocity and azimuth values over the 2015–2100 period is compared with the trend from these in situ observations. This is done as observations of the recent past and simulations of the near future are the best available data for each respective period. Comparing past observation-based trends with modeled future trends is standard practice as using past observed trends can textualize future model trends (e.g. Fig 9.17; Fox-Kemper and others, 2021).

Velocity and azimuth have previously been surveyed by three independent campaigns. The first measurements were originally conducted as part of the French Expédition Glaciologique Internationale Groenland (EGIG) campaign in 1959 and 1967, which surveyed an east–west transect of the ice sheet (Heimes and others, 1986). During the 1990s, the NASA Program for Arctic Regional Climate Assessment (PARCA) conducted a survey of velocity and azimuths along the 2000 m elevation contour line, crossing the transect surveyed by the EGIG campaign (Thomas and others, 1998). A subset of sites from both of these campaigns were later resurveyed in an independent campaign in 2020–2022 (Lükkegaard and others, 2024). In this study, we discuss observations from ten of these sites, located ~100 km inland, outside any channelized flow. See Figure 8 for an overview of the sites.

Figure 8. Overview of observation sites in relation to the observed catchments, zoom in of Figure 1. The map units are projected coordinates in kilometers, using the north polar stereographic projection EPSG: 3413.

The trend in observed and modeled change in velocity and azimuth values is compared in Figure 9. Absolute velocity and azimuth values are shown in Supplementary Figure S7. Note that the plotted time range starts in 1995 where the observations show a relevant change (Lükkegaard and others, 2024). These EGIG and PARCA measurements will be referred to as the baseline observations characteristic of c. 1995. The mean trend of all ten sites is evaluated, representing a general region close to the northern catchment boundary. This is because re-interpolations of velocity grids, first from native model resolution to common 5 km ISMIP6 grid resolution, and subsequently to specific baseline observation sites, can introduce uncertainties. Each model, however, is consistent with the regional average for site-by-site comparison. Supplementary Figures S8–S11 show site-by-site comparison of the modeled and observed easting and northing velocity components, total velocity magnitude and the azimuths for each of the 13 models.

Figure 9. Comparison in trend of modeled and observed (a) velocity and (b) azimuths at the ten sites. The gray box denotes available baseline observations (EGIG and PARCA) from the first observational period, blue box denotes observations of the ten sites from the second observational period. Here, the width of the box represents the time span over which observations are representative, the height is the range of observed values, and the white line the mean value of all ten sites. Colored lines show the mean velocity or azimuth respectively of all ten sites, for each member of the ISMIP6 ensemble. Note all values are normalized to 2020 values.

Baseline velocity observations at the ten sites were found to have accelerated over time, ranging between ~3.9 and 10$\%$ per decade. Figure 9a shows the model ensemble mean underestimates this regional acceleration in ice flow. The ISMIP6 ensemble mean change in velocity starts slow and speeds up, almost reaching the observation-based trend in velocity change toward the end of the modeled period (2100). However, this increase in velocity is modeled to occur over a much longer timescale compared to the observed increases in velocity. The ensemble mean change in velocity in Figure 9a is not linear between 2015 and 2100, however, in order to compare the trend in the simulation- and observation-based change in velocity the trend in the ISMIP6 ensemble mean changing velocity is to a first approximation assumed to be linear. The slope of the modeled trend line is approximately half of the observed trend line. This suggests that the ISMIP6 ensemble is underestimating the deep inland dynamic response of the ice sheet to the recent climatic changes.

Observations show a consistent increase in azimuth values across the EGIG sites of ~3 − 4.5°, meaning a northward deflection of the ice flow. In comparison, the PARCA sites cd38 and cd08 showed a slight decrease in azimuth values of ~1°, which is within the ±2° error-bound of the PARCA observations. The ISMIP6 ensemble mean change in azimuth, shown in Figure 9b, only shows a change of ~1° over a period of 86 years. This suggests that the position of the modeled northern catchment boundary is less sensitive to change in comparison with observed azimuth changes. Figure 9b also shows that the modeled ensemble has the opposite trend in azimuths, compared to the observed change in azimuths, meaning a regional southward deflection of the ice flow. The ISMIP6 ensemble suggests that this translates to a northward migrating catchment boundary. As the ISMIP6 ensemble underestimates ice flow acceleration, this indicates an insensitivity to changes in easting and northing ice flow velocity components. This in turn means changes in the azimuth would be similarly limited. If the models captured the acceleration better, the trend in azimuth might be better captured.

Assessing catchment boundary migration reflects complex changes in easting and northing components of ice flow. There is an appreciable ‘along-divide’ flow component, meaning that the catchment boundary migration can be a result of very small flow component deviations. However, northward migration of the boundary is consistent with the decreasing azimuths. A parcel of ice within the catchment close to the boundary will experience a southward pull as the northing velocity component increases southward, leading to more ice being pulled into the catchment, and the boundary (which has a theoretical topographical high point) will move in the opposite direction. Figure 10 shows a schematic of the catchment migrating northward, as the azimuth at a given point decreases over time.

Figure 10. Theoretical schematic of changing azimuth and migrating catchment boundary in the vicinity of our in situ observations. Here dotted t ₁ and t ₂ lines denote the catchment boundary positions at initial (t ₁) and later (t ₂) timesteps. The correspondingly colored arrows show the change in azimuth, with the yellow point visualizing an arbitrary point within the catchment.

It is difficult to evaluate whether the ‘true’ catchment in that case is migrating southward, as the in situ observations show ice flow deflecting northward. If that was the case it would suggest that the area of the catchment is becoming smaller at least along the northern side. Interpretations of the observed trends could be influenced by which side of the catchment the observation sites are located (in terms of the ‘true’ catchment). Therefore, it poses a problem that some of the observation sites are located so close to the estimated northern catchment boundary, and could potentially be outside the Sermeq Kujalleq catchment. However, the consistencies in trend between all the EGIG sites located along both the north-south and east-west transects suggest the sites are most likely on the same side of the boundary.

Although the specific cause behind the ISMIP6 ensemble catchment migration is unclear, we are aware of some factors that could result in the difference between observed and modeled trends. First, as previously mentioned, the initialization method has a big impact on the final simulations. Real-world ice is presently responding to the combined effect of multiple climate forcings over a range of time periods. For example, Sermeq Kujalleq is known to have experienced large changes in the last 30 years. The dynamic response of these changes are not included in the ISMIP6 simulations, as they have been initialized and run to match the 2015 velocities, as if the 2015 state was in transient equilibrium.

Second, as mentioned earlier, ice flow models can have problems capturing fast ice flow velocities for a variety of reasons. Lükkegaard and others (2024) theorized that changes in the basal temperate layer in the region, resulting from creep instability, could be the reason for the observed accelerated ice flow and change in ice flow direction. It is notoriously difficult to implement non-diffusive heating mechanisms in ice flow models and accurately capture the full ice column temperature profile. The general difficulty in fully representing such mechanisms in the ISMIP6 ensemble could also explain the discrepancy between model and observed flow trends.

4.3. Understanding modeled temporal catchment variability

4.3.1. Future evolution

The ISMIP6 ensemble suggests that the Sermeq Kujalleq catchment will expand under the high-emission scenario even under various levels of ocean forcing. The largest relative change in catchment over time was produced by model UCIJPL ISSM1, showing an increase of 14.4, 10.2 and 4.1% for the ‘high’, ‘medium’ and ‘low’ ocean forcing experiments, respectively. Only the ‘low’ ocean forcing simulations had three model runs showing a slight decrease in catchment area from start to finish. However, the mean change in area of the ensemble from 2015 to 2100 shows an increase of [2.7, 5.7, 9.1]% under the three ocean forcing scenarios, see Figure 5. Considering this change in catchment area cumulates over an 85-year time frame, it is relatively small in comparison to the present-day deviation between catchments, solely based on the choice of delineation method ± 12%. This means that the uncertainty in the mass-balance estimates caused by temporal variability of the catchment will likely not be as influential as the initial catchment delineation. To a first approximation, it is expected that the effect of not taking the temporal variability of the catchment into account on the SMB estimates will be approximately proportional to uncertainty in SMB ([2.7, 5.7, 9.1]%). However, since the models seem to underestimate the recent acceleration of inland ice flow (at least at Sermeq Kujalleq), this may suggest they are not sensitive enough to accurately represent far inland changes currently happening on the ice sheet. Perhaps more sensitive ice flow models would yield greater catchment expansion. In any case, there does seem to be an argument for considering the temporal variability of major ice-sheet catchments on decadal timescales. Therefore, catchment-scale SMB studies estimated over longer timescales both forward (e.g. Box and others, 2022) and backwards in time (Kjeldsen and others, 2015; Khan and others, 2020) might need to consider adding an uncertainty related to the change in the catchment area, even though this uncertainty will most likely be small relative to the uncertainty in SMB.

We do see variation in estimated change in area across the ensemble of models, as seen in Figure 5, but no clear pattern indicates which ‘type’ of model is more sensitive than others. There are several factors that can influence the flow regime, and hence the delineated catchment. As mentioned previously, the models vary in the way they have been initialized. Some models used various nudged paleo-spin ups, to best capture flow, form and thermal state, while others used data assimilation, assuming the temperature field is in equilibrium with present-day conditions, and others used a combination of assimilation and spin up by creating the temperature field separately using the paleo-spin up method. Unfortunately, the 3D temperature fields of the ISMIP6 ensemble are not publicly available to be evaluated. Only the 2D surface and basal temperature fields are available. These basal temperature fields are evaluated by MacGregor and others (2022), who generally find a warm-bedded thermal state throughout most of the Sermeq Kujalleq catchment across the ISMIP6 ensemble. In addition to differences in horizontal grid resolution, the vertical resolution also influences how well the vertical temperature profile is captured. Some models include higher-order stresses while others use the SIA/SSA hybrid approximations. This will have an effect on how processes at the calving front are transmitted further inland.

There seems to be an asymmetry in the temporal variability of the northern and southern catchment boundary. The larger movement seen in the southern catchment boundary, Figure 6a, makes sense since the adjacent glaciers immediately south of Sermeq Kujalleq are mainly land terminating. The glaciers north of Sermeq Kujalleq are primarily marine-terminating outlet glaciers, and likely to be responding in a similar fashion as Sermeq Kujalleq to the high-emission scenario. The catchment south of Sermeq Kujalleq, which has less dynamic land-terminating glaciers, seems to become smaller at the expense of the increasing area of Sermeq Kujalleq catchment. This supports the theory of Bindschadler (1984), who theorized that basin boundary migration would result in response to changes in relative discharge rate of adjacent catchments as they compete for the inland ice. Following the terminology from Carter and others (2013), we suggest a dynamic piracy of the ice flow is taking place. The land-terminating ice south of Sermeq Kujalleq will thin more rapidly, as its upstream dynamic supply is shifted north toward Sermeq Kujalleq.

4.3.2. Limitations of the simulated catchments

To examine the potential temporal variability of the Sermeq Kujalleq catchment, this study delineated catchments from many timeslices of modeled surface velocities. The model grid resolution, however, will unavoidably influence the final area of the delineated catchments. The model ensemble consists of models using both finite element and finite difference solvers, and the choice in original individual model grid resolutions varies noticeably. The finite element grids are occasionally large inland, in some cases defined to 25 or 30 km. This means that the grid resolution can become greater than the modeled change in catchment boundary. In this case, the models might not be sensitive enough to fully capture the change in catchment. Finite difference models, on the other hand, generally are less able to capture the fine changes that happen at the very front.

The ISMIP6 publicly available velocity fields are interpolated from various native grid resolution to a common 5 km grid. Delineating the simulation-based catchments therefore requires interpolation between already interpolated points. This undoubtedly results in position errors in our delineated catchments. Furthermore, since the flowlines are started at the margin of the ice sheet the error in the flowline position will accumulate upstream.

Another influence on the final delineated catchments, which occurs when using simulated ice flow velocities, is the potential that some changes result from model drift. As described in section 2.2, the ISMIP6 campaign also included control runs for each projection run. The catchments were also delineated for the model ensemble control runs, and the resulting relative change in area can be seen plotted together with the relative area change of the three experiments in Supplementary Figure S12. Although we do see change in the catchment area in the control runs for the individual models, the change is generally smaller than that seen for the exp05 runs. The change in exp05 runs is therefore not assumed to be model drift alone. The catchment does seem to have some variation in time, which is consistent across ensemble members.

5. Conclusion

It appears likely that Sermeq Kujalleq's catchment will slightly change area/shape in response to the currently anticipated range of future climate forcings. This, in turn, has the potential to influence our assessment of catchment-scale input–output mass-balance estimates.

Firstly, we evaluated 16 ice-sheet models’ ability to capture the shape and size of the catchment of Sermeq Kujalleq. This was done by comparing catchments delineated from the historical ISMIP6 experiments, representing the ‘present day’ (2014) state of the GIS, against observationally delineated catchments generally regarded as representative of ‘present day’ (published in the past 15 years). Various methods were used to delineate these observed catchments. The community ice-sheet models were found to be able to capture the catchment fairly well, in both shape and size, across the ISMIP6 16-model ensemble. The ISMIP6 ensemble mean area was found to be $\sim 6.3\%$ larger than observed, even when excluding part of the modeled catchment area. However, the spread in both modeled ($\pm 15.4\%$) and observed ($\pm 12.3\%$) delineated catchments was found comparable in size, meaning that although the ISMIP6 study was not designed for catchment-scale studies, community ice-sheet models are still able to capture Sermeq Kujalleq catchment area with the same amount of uncertainty as catchments delineated from observations.

Secondly, the potential temporal evolution of the catchment was examined by delineating the catchment for annual time slices for a 13-model ensemble, covering the period 2015–2100. Simulated Sermeq Kujalleq behavior seems to be exhibiting dynamic piracy, expanding along the southern boundary at the expense of ice flow to more southern land-terminating glaciers. The ISMIP6 ensemble showed a catchment area expansion of $\sim [ 2.7,\; \, 5.7,\; \, 9.1] \%$ by the year 2100 under the RCP 8.5 high-emission pathway. This indicates that, the ‘true’ catchment is not strictly temporally invariant, as is often implicitly assumed. It is likely changing in a measurable way, although this change is small in comparison to uncertainty in catchment area across the six-member available observational ensemble. Therefore, agreeing on common present-day catchment, although difficult, seems more important for limiting error in input–output estimates, than capturing the temporal evolution of the catchment. The variation in the area of the observed catchments resulting from different delineation methods and choice of observations alone ($\pm 12.3\%$) is greater than the temporal variability of $\sim [ 2.7,\; \, 5.7,\; \, 9.1] \%$.

It has to be noted, however, that this temporal variation might be underestimated. A regional comparison between observed and modeled ice flow velocities showed insufficient ice flow acceleration across the ensemble. Also, simulated regional flow direction was found to have opposite trends from observed flow direction. This undoubtedly will have some effect on the delineated catchments. Although the uncaptured regional trend in both acceleration and flow direction at far inland sites upstream of the outlet of Sermeq Kujalleq might be due to the models not having been forced correctly, e.g. at the ocean boundary during the final part of the historical run, it could also be necessary to focus on some key model processes. Stress balance approximations and higher-order implementions seem to produce the same regional trend and comparable magnitudes of flow. Either the higher-order implemention is still not fully capturing and transmitting downstream force-balance changes, and the full-Stokes solution is necessary, or perhaps the focus should be on implementing specific softening mechanism(s), such as cryo-hydrological warming and thick basal temperate layers in the models. This comparison between modeled and observed flow highlights the value of independent in situ observations to evaluate ice-sheet model simulations. Observations might also be the only way to define which model and/or delineation method most accurately captures the ‘true’ catchment.

This study only looked at the catchment of Sermeq Kujalleq. A future community goal could be to delineate catchments for the full ice sheet for both the Greenland and Antarctic ice sheets. A nested standardized catchment product appears to be a necessary community goal, to allow intercomparison of catchment-scale input–output estimates from different studies, without delineation errors. Potentially, a product with regular temporal updates, similar to what has been demonstrated for ice-sheet masks used in mass-balance studies, to decrease error in the final mass-balance estimates. This could provide insight into potentially more sensitive or temporally varying catchment boundaries, which in turn could be used to identify locations to survey with precise GPS instruments on longer timescales measuring inter annual acceleration and flow direction. In the future, when working toward a common catchment product, it seems the focus should be on methods not only using ice surface DEMs to delineate the catchments.