Introduction
It is commonly accepted that at low strain rates snow deforms in a ductile manner while at higher strain rates snow deforms in a brittle manner (e.g. Reference McClungMcClung, 1979; Reference SchweizerSchweizer, 1998). Accepted values for the ductile–brittle transition range from ∼1 × 10−3 to ∼1 × 10−4 s−1 depending on snow type. Far less consideration has been given to the rate dependence of fast-moving deforming objects, such as snow penetrometers (e.g. Reference Schneebeli and JohnsonSchneebeli and Johnson, 1998; Reference Mackenzie, Payten and StevensMackenzie and Payten, 2002), where most of the deformation may be assumed to be already in the brittle regime. This paper focuses on how penetration rate affects the force response of a manually driven, round-tipped digital penetrometer. Such devices are used for analysing snow stratigraphy and have applications in avalanche forecasting and hydrology.
Several studies have tried to assess rate effects for fast-moving snow penetration and have drawn differing conclusions. Reference GublerGubler (1975) performed experiments with a rammsonde penetrometer using sieved snow of an unspecified density. He reported a strong rate effect, with mean hardness values decreasing by approximately one order of magnitude as penetration velocities increased from 6.8 × 10−3 to 65 cm s−1 . Reference FukueFukue (1977) deformed uniform snow samples at different rates in a cold laboratory using a thin blade. His experiments show an asymptotic relationship between force response and velocity, although the number of data points at higher velocities was quite low. Reference FederolfFederolf (2005) deformed snow samples in a decelerating regime using an instrument called the ‘Fast Snowdeformer’. The force on a free-falling piston and its displacement were recorded during impact for a variety of initial impact velocities on dense, well-sintered snow ranging from 420 to 525 kg m−3. His results showed a flat response between piston velocity and the impact force per metre.
In the experiments above (with the possible exception of those of Reference FukueFukue, 1977) analysis was confined to the initial stages of snow deformation. Reference JohnsonJohnson (2003) noted that compaction of material ahead of a penetrometer tip initially proceeds at a low force until the density of the compacted material reaches a critical state. At this point, the material fragments lock up and no further compaction is possible; this snow must be moved aside or pushed ahead of the penetrometer. Reference JohnsonJohnson (2003) termed the region of compacted snow the compaction zone and the perimeter of this zone the penetrometer effective surface (PES). An object inserted into uniform snow therefore experiences two phases of deformation: an initial transient phase, where the compaction zone develops beneath the object, and a steady-state phase, where the relative positions of the tip, compaction zone and deforming front remain constant. The deforming front defines the perimeter of a region we term the deformation zone, encompassing the entire region of plastic deformation. Similar phases of deformation have been identified for penetrometer insertion in soils (e.g. Reference Huang, Sheng, Sloan and YuHuang and others, 2004; Reference Walker and YuWalker and Yu, 2006).
While no formal theory for snow penetration by a round-tipped penetrometer has been presented, it seems reasonable that some characteristics will be shared with conical penetration into snow, for which theory is better developed (Reference Johnson and SchneebeliJohnson and Schneebeli, 1999; Reference JohnsonJohnson, 2003). The force exerted on the penetrometer tip depends on the number of microstructural elements in contact with the PES and the average rupture force required to rupture bonds between microstructural elements as well as ice–tip and ice–ice frictional components. The PES depends on the diameter of the tip, microstructural snow properties and also, importantly, cone angle. As the cone angle exceeds 120°, which is the case over the central portion of a round-tipped penetrometer, penetration resistance was found to increase dramatically. Observations of deformation by flat plates (cone angle 180°) (Reference YosidaYosida, 1956; Reference Fukue and YongFukue and Yong, 1987; Reference Gleason and ElderGleason, 2005) confirm that a plug of compacted snow is pushed ahead of a flat object as it is pushed through the snow. The reactive force against the flat plate itself must therefore be transmitted from the undisturbed snow via the compacted snow onto the plate.
Round penetrometer tips have been more commonly associated with soil penetrometers. Reference GillGill (1968) observed that soil bodies were liable to form on blunt penetrometer tips, including spherical tips. Reference Mulqueen, Stafford and TannerMulqueen and others (1977) deformed clay and sandy soils with 10 mm, 30° conical and 10 mm rounded penetrometer tips, and found that for relatively low-density soils, penetration resistance for the rounded tip was significantly higher than for the conical tip. As soil densities increased, the differences between the tips decreased. High soil moisture content also decreased the difference between the tips. Reference Smith and MullinsSmith and Mullins (2001, p.379) state that soil builds up on probe tips when the tip angle exceeds 90°. Reference White and BoltonWhite and Bolton (2004) determined displacement and strain fields for soil deformation beneath flat-ended, square-based piles driven into sand using particle image velocimetry (PIV). They concluded that strain paths are initially vertical in compression, followed by horizontal movement associated with shear as the soil elements flow around the pile shoulder.
In this study we present results from field experiments designed to measure how the force response on a round-tipped penetrometer varies with velocity for in situ snow samples of low to medium density (∼100–350 kg m−3). Studies on in situ field samples are under-represented in the literature, despite the fact that these samples are closer to the range of densities associated with avalanche slabs (Reference McClung and SchaererMcClung and Schaerer, 2006, p.92) than the laboratory-processed snow used in many studies. We focus here on higher velocities that are consistent with those attained when driving a penetrometer manually into the snow. We also present an analysis of how snow deforms around the penetrometer tip from deformation experiments performed in a clear plastic box. This analysis is presented because it aids our interpretation of the results of the rate-effect experiments.
This study principally has implications for developers of manually driven force-resistance snow penetrometers. Such instruments have the potential to be lighter and more portable than those driven at a constant velocity by a mechanical drive. However, they suffer from unavoidable variations in velocity as they are pushed through the snow.
Methods
Rate effects
We used a manually driven SABRE penetrometer (Reference Mackenzie, Payten and StevensMackenzie and Payten, 2002), designed and built by Himachal Safety Systems, Inc., to measure the force response of snow in this study (Fig. 1). The SABRE penetrometer was driven horizontally at a range of velocities into four different thick, uniform snow layers. The number of pushes into each layer ranged from 18 to 30 and velocities up to 120 cm s−1 were attained. The properties of the tested layers are given in Table 1.

Fig. 1. Apparatus for performing rate-effect experiments. The SABRE penetrometer (A), guided by the displacement platform (B), was pushed horizontally into a thick, uniform snow layer (C). Data were recorded on a data logger (D).
Table 1. Snow properties for the layers used for the rate-effect experiments

A piezoelectric sensor inside the SABRE penetrometer measured the force response from a 12 mm diameter, rounded stainless-steel tip. This signal was electronically amplified to give an output in millivolts. The relationship between the amplified output signal and the applied force was found to be approximately linear over the range of forces used (Reference FloyerFloyer, 2008). This linear relationship, which is specific to this device and therefore not reported here, was used to convert the output voltage to a force response in newtons.
A custom-built displacement-measuring platform (Reference FloyerFloyer, 2006) employing a high-friction encoder wheel with a diameter of 200 mm and a resolution of 0.2 mm was used to measure the horizontal displacement of the penetrometer; this also served as a guide to keep the penetrometer within the layer of interest. The supplied data-collection device from the SABRE penetrometer was not used; instead, the amplified output from the piezoelectric sensor was recorded at 1000 Hz with a Campbell Scientific CR1000 data logger. The same data logger was used to record the horizontal displacement, although, due to equipment limitations, this was at a lower rate of 100 Hz. The displacement signal was interpolated to 1000 Hz using a cubic convolution interpolation method (Reference Park and SchowengerdtPark and Schowengerdt, 1983) within the Interactive Data Language (IDL). Mean velocities (and corresponding mean force values) were averaged over distances of 1 cm or a minimum of 20 force measurements. This latter criterion ensured that, for higher velocities, at least two measured displacement points were used for velocity calculations, preventing oversampling of the interpolated displacement signal.
Snow deformation
Additional apparatus (Fig. 2) was used to analyse snow deformation at the penetrometer tip. A clear, stiff plastic box of dimensions 30 cm × 20 cm × 5 cm with removable sides was filled with snow from a uniform layer at least 7 cm thick. In order to fill the box with minimal snow compaction, two of its sides were removed before being pushed horizontally into the snow layer and cut out using a metal spatula. The snow on one side was ‘seeded’ with chilli flakes (diameter ∼2–5 mm), before the box side was replaced and the box oriented such that the seeded side was vertical. A split-axis stainless-steel rod with a tip of the same size and shape as that of the SABRE penetrometer was pushed vertically through the snow against the side with the chilli-flake markers. The process was recorded using a video camera at a frame rate of 30 fps. The resolution was 2–3 pixels mm−1; the variation was due to different distances between the snow box and the video camera. The snow layers used in the deformation experiments were different from those used in the rate-effect experiments and are described in Table 2.

Fig. 2. Diagram of apparatus for analysing snow-deformation patterns around the penetrometer tip. A split-axis rod (A) was pushed manually into a snow box with removable sides (B) that was filled with uniform snow and seeded with chilli flakes (C). The pushes were recorded with a video camera (D). A ruler fixed to the side (E) was used to convert deformation vectors from pixels to millimetres.
Table 2. Snow properties for the layers used for the snow-deformation experiments

PIV (Reference Crocker and GrierCrocker and Grier, 1996) was used to analyse the deformation patterns from videos of the snow box. The IDL routines used in the PIV analysis were modified versions of those used by Crocker and Grier. The chilli-flake markers in the snow were tracked from frame to frame to generate a displacement vector field, D, for each frame pair:
where A is the position field for all detected particles and i is the frame number. Since the routines identify marker particles based on their size, ellipticity and brightness, chilli flakes, which have a range of sizes, shapes and colours, are well suited to this task. A maximum interframe displacement was specified to reduce the chance of erroneous particle tracking.
Camera shake was identified as a problem in several of the pushes. This was corrected by applying a rigid-body transformation (a translation and a rotation) to each successive pair of frames in the affected pushes. The corrections were determined from the undeformed particles in each frame pair; these were specified as particles that moved less than a certain threshold and also lay further than a specified distance away from particles that did exceed this displacement threshold. The required transformation, T, is a Procrustes transformation (Reference SchönemannSchönemann, 1966) that least-squares minimizes the residual matrix, E:
where B is the position field of the undeformed particles. The problem is equivalent to maximizing the trace,
![]() and can be solved using singular value decomposition (e.g. Reference Golub and van LoanGolub and van Loan, 1996, p. 70) to set:
and can be solved using singular value decomposition (e.g. Reference Golub and van LoanGolub and van Loan, 1996, p. 70) to set:
where U and V are unitary and S has singular values down the diagonal. Reference SchönemannSchönemann (1966) showed that the optimum transformation may be obtained from
The corrected displacement field was calculated by applying the transformation to the uncorrected data:
For some parts of the analysis, the corrected displacement field from Equation (5) was used directly. For other parts, the (corrected) total deformation field was used:
where ΔX and ΔY represent particle movement in the x and y directions, respectively, over the number of frames being considered.
Results
Rate effects
A typical force/displacement plot (Fig. 3) shows a spike near the start of the push and then settles to an almost uniform level (flat portion), despite variations in the velocity during the push. The force varied considerably between pushes into different types of snow, as expected. There were also smaller variations between pushes into the same snow layer. To account for these within-layer variations, the difference between the flat portion of the individual trace and the mean flat portion of the layer was subtracted from each trace.

Fig. 3. Typical force (solid curve) and velocity (dashed curve) trace for dry pencil-hardness snow.
Each normalized force/displacement trace was sampled many times; each sample comprised mean force and velocity values averaged over 20–100 data points. This acted to smooth local variations in the force signal and allowed the differentiation of a sufficient number of displacement values to give a reliable local velocity value. Figure 4 shows the sampled force/velocity pairs from all traces into each layer, including pairs taken from the spike at the start of each trace. Force values increase as the hardness and density of snow increases, as expected. Note that the jump in the force response from 1-finger snow to pencil snow (0.64 N to 5.2 N) was found to be far greater than the jump from 4-finger snow to 1-finger snow (0.38 N to 0.64 N), despite there being one hardness step in each case.

Fig. 4. Combined force/velocity pairs (all data used) for all traces for (a) dry pencil-hardness snow, (b) moist pencil-hardness snow, (c) dry 1-finger hardness snow and (d) dry 4-finger hardness snow.
For both pencil-hardness snow layers (Fig. 4a and b) there are considerable spikes in the force response at lower velocities: at 5–15 cm s−1 for the dry pencil layer and 15–30 cm s−1 for the moist pencil layer. There are smaller, far less pronounced spikes at ∼10 cm s−1 for the 1-finger and 4-finger layers (Fig. 4c and d). The moist pencil layer (Fig. 4b) shows considerable variation in force values, even for higher velocities, which is in sharp contrast to the dry snow layers that level off to a smooth level at higher velocities. This is probably due to successive bonding and release of snow at the head of the compaction zone caused by the elevated moisture content, a phenomenon known as ratcheting (e.g. Reference Hassan and KyriakidesHassan and Kyriakides, 1992).
It was suspected that the spike in the force response might be due to the development of the compaction zone in the transient phase of the push. To test this suggestion, up to 6 cm of data from the start of each push was removed (less was removed if the spike occurred sooner, and none was removed if there was no spike). Since a wide range of push velocities was used during the experiments, many of the low-velocity data points still remained for each layer, with the exception of the moist pencil layer, for which no data less than 5 cm s−1 remained.
Figure 5 shows the force/velocity response for the modified datasets. Both pencil-hardness layers show a considerable reduction in the magnitude of the low-velocity spike, with the removal of early-push data. For the moist pencil layer, considerable variations in force with velocity remain, due to the ratcheting effect previously described. The 1-finger and 4-finger layers remain largely unchanged, since the low-velocity spike is not very pronounced for these layers.

Fig. 5. Combined force/velocity pairs with early-push spike data excluded for (a) dry pencil-hardness snow, (b) moist pencil-hardness snow, (c) dry 1-finger hardness snow and (d) dry 4-finger hardness snow. Regression lines and coefficients are shown on each graph. R 2 = 0.99 for (a), (c) and (d); R 2 = 0.96 for (b).
Snow deformation
Figure 6 shows deformation patterns around the penetrometer tip for the 4-finger dry snow (layer 1). In this image the coordinate system is altered so the particle movement is relative to the penetrometer tip. This was achieved by digitizing the location of the penetrometer tip in each frame. The image combines displacement vectors from successive frame pairs for frames where steady-state deformation was established. In this way, vectors are generated that appear to ‘flow’ around a stationary penetrometer tip. It may be helpful to imagine keeping the penetrometer stationary and bringing up the snow to meet the penetrometer. The deformation zone (region where any amount of deformation takes place) extends just over 2 cm ahead of the penetrometer tip. There is evidence for the compaction zone from vectors that diverge ahead of the penetrometer tip.

Fig. 6. ‘Flow vectors’ for dry 4-finger hardness snow, ρ = 137 kg m−3, showing the movement of indicator particles relative to the tip.
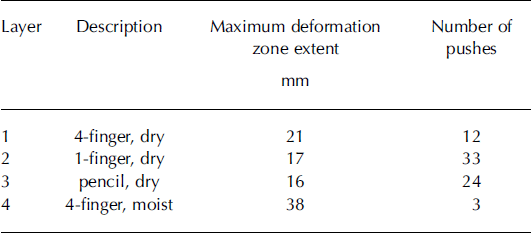
Table 3 shows the maximum extent of the deformation zone for each of the four layers tested. With the caveat that the number of samples is small, for dry snow the size of the deformation zone appears to decrease slightly as the snow hardness increases for the layers tested. In contrast, the moist snow layer tested had a much larger maximum deformation zone extent, and was seen to be more erratic in the unprocessed videos, appearing very large in some frames and almost nonexistent in others.
Table 3. Maximum extent of deformation zone for the four snow layers described in Table 2
In order to analyse the formation of the deformation zone, the early frames from the snow-box videos were considered in more detail. Figure 7 shows the total deformation field ahead of the penetrometer tip at ∼10 mm intervals for the first 80 mm of insertion. Even after the first 10 mm the deformation zone is quite well developed, extending ∼10 mm ahead of the tip. After 50 mm of insertion the deformation zone appears to have grown to approximately its maximum extent and does not become appreciably larger. The light-coloured areas in Figure 7 are regions that are moving at approximately the same speed as the penetrometer tip, and therefore indicate the extent of the compaction zone. This appears to be best developed in the final three frames.

Fig. 7. Deformation sequence during the transient phase of compaction zone development. Images are spaced approximately every 10 mm and the total deformation field was calculated over the preceding 10 mm of insertion. Shading shows total deformation, with light-coloured areas indicating greater deformation.
The images in Figure 7, along with similar images for the other snow layers tested, were further processed to estimate the size of the deformation zone as it was developing. The cross-sectional area of a slice through the centre of the deformation zone was estimated by interpolating the total deformation field onto a regular grid and integrating the region under the penetrometer tip that exceeded 1 mm of total displacement for 10 mm of penetration. The threshold of 1 mm was necessary to distinguish genuine displacement from noise generated by camera shake and other limitations in the particle-tracking routines. Therefore, the cross-sectional areas are probably slightly underestimated. Despite this, it is a reasonable metric for comparing the size of the deformation zone between frames.
Figure 8 shows how the cross-sectional area of the deformation zone changes as the penetrometer is inserted into the snow. The three dry snow layers show similar trends: the deformation zone fairly quickly reaches a maximum extent and then appears to level off at an approximately constant value. Note that the 1-finger snow required more penetration before reaching a steady state than the 4-finger and pencil-hardness snow. The moist snow layer shows different behaviour to the dry snow layers, with the cross-sectional area of the deformation zone fluctuating widely as the penetrometer tip is inserted. The moving average trend line shows two pulses where particularly sizeable plugs of snow were pushed ahead of the penetrometer tip. This pulsed deformation of snow ahead of the tip is direct evidence for the ratcheting process mentioned above.

Fig. 8. Relative deformation zone size represented by the cross-sectional area of a slice through the centre of the total deformation field at different insertion depths for (a) layer 1, 4-finger dry snow, (b) layer 2, 1-finger dry snow, (c) layer 3, pencil dry snow and (d) layer 4, 4-finger moist snow. Dashed curve in (a–c) represents a visually interpreted trend. Dashed curve in (d) represents a two-point moving average.
Discussion
During initial stages of compaction zone formation, shear stress is concentrated in a cylindrical zone below the penetrometer tip. The applied force increases until the shear stress exceeds the strength of the compacted snow. When the contact strength between grains is high, as is the case for hard and moist snow, the applied force goes through a maximum before exceeding the strength of the snow and a spike appears in the force-response curve, as seen in the pencil-hardness layers in this study (Fig. 4a and b). This response is consistent with results from soil penetration when vertical pressure is high (Reference Huang, Sheng, Sloan and YuHuang and others, 2004), which is the case for dense or saturated soils. The low-velocity spike for the pencil-hardness layers is virtually eliminated when the transient push component is removed, which indicates that this spike relates to the initial development of the compaction zone. When the contact strength between grains is low, which is the case for the less-resistant snow, the spike in the force-response curve is not seen (Fig. 4c and d).
The size of both the (fully densified) compaction zone and the (partially densified) deformation zone depends on the initial uncompacted density of the snow and the resistance to grain rearrangement. Grain rearrangement is controlled by the packing behaviour of displaced fragments and the degree to which fragments can penetrate void spaces (Reference JohnsonJohnson, 2003). Large or angular grains and grains that undergo rapid re-sintering (Reference Szabo and SchneebeliSzabo and Schneebeli, 2007) will experience greater resistance to grain rearrangement and result in larger compaction and deformation zones. The extent of the deformation zone for the different dry layers in this study (Fig. 8) was quite consistent, actually increasing slightly for less-resistant snow. The larger or more angular grains associated with less-resistant snow appear to have counteracted the higher initial density of the harder snow, resulting in slightly larger deformation zones for the low-resistance dry snow layers.
In the rate-effect experiments, all the dry layers show a greater range of force values at lower velocities than at higher velocities. This indicates that rate effects may play a small, albeit far lesser, role by influencing the variability of the force response. There should be some caution with this interpretation, however, since there are fewer data points at higher velocities.
Regression lines were fitted to each layer and are shown on each graph in Figure 5. The gradient of these lines ranges from −4.6 × 10−4 to 3.0 × 10−4 N s m−1, an almost flat response for each layer. In general, we can say that, once steady-state deformation is reached, force values vary very little with velocity for the range of velocities in our experiments. In moist snow, far more variability in the force value is likely to be encountered, but there is still no relationship between the force and velocity.
The method for calculating the cross-sectional area of the deformation zone has two potential problems. First, in some frames, only a small number of vectors appear in the deformation zone. This occurs when the penetrometer tip passes through a region where the chilli-flake density is relatively low. This gives rise to the possibility for interpolation errors, with a greater likelihood of underestimating the size of the deformation zone. Second, particle misidentification could lead to a spurious region of deformation. This would probably result in an overestimation of the deformation zone. The outliers in Figure 8b and c are probably a result of these issues. Overall, however, the method appears to give a reasonable estimate for comparing the extent of the deformation zone from the snow-box videos.
The formation of the deformation zone (and by extension the compaction zone) in dry, pencil-hardness snow took ∼6 cm in the deformation experiment. This was consistent with the length of the penetrometer profile that was removed to eliminate the early-push spike from the force-resistance signal in the rate-effect experiment for a similar pencil-hardness snow layer.
In the snow-deformation experiment it is not clear why the deformation zone took longer to develop in the dry 1- finger snow layer than in the dry 4-finger and pencil-hardness layers. Possibly, there was a cavity near the top of the snow box created when it was filled with snow, or else the chilli-flake density could have been low, giving rise to the gridding problems mentioned above.
Although our results apply to round-tipped penetrometers, which are not widely used for snow stratigraphy evaluation, it is useful to consider how these results might be extended to the case of conical penetrometers, which are more widely used. Reference JohnsonJohnson (2003) has shown that the compaction zone for a conical penetrometer whose cone angle is 60° or less does not extend far below the penetrometer tip and may be modelled as a conical shape having a cone angle slightly larger than that of the tip itself. The fact that a compaction zone does exist means initial compaction and subsequent exceedance of snow strength is possible, giving rise to early-push force spikes. However, the small size and vertical extent of the compaction zone is likely to limit this effect to snow of considerably higher density compared with the round-tipped penetrometer. Once steady state is reached, the force response with velocity is likely to be flat, although at a lower force level, due to the reduction in the perimeter effective surface.
Conclusions
We find no dependence of the force response on velocity over the velocity range tested, provided that (up to) the first 6 cm of penetration is excluded from the analysis. We conclude, therefore, that a manually driven penetrometer does not suffer from rate effects caused by variations in velocity during its push, except initially in hard slabs, or possibly if a very rapid transition in snow hardness is encountered. Further work is necessary to confirm the latter case.
During the first 6 cm of displacement (for a rounded 12 mm diameter tip), pronounced spikes in the force response were noted for higher hardness layers. This was attributed to the development of a compaction zone: a zone of densified snow pushed ahead of the tip and characterized by a slow turnover of snow material. The development of such a zone was inferred from snow-deformation experiments, and the distance taken for the development of this zone was consistent with the location of the spike in the rate-effect experiments.
Compaction zones developed in all snow types tested. However, their development had a greater influence on the force response for high-resistance snow layers. The size and extent of deformation zones (zone encompassing all deformation) was easier to measure than that of compaction zones. Preliminary results suggest that, for dry snow, these are larger for soft snow than for harder snow. Deformation zones in soft, moist snow were found to be particularly large due to the combination of enhanced capillary cohesion due to the presence of free water and the low strength of the surrounding snow. Ratcheting, where the compaction zone cyclically grows and collapses, was directly observed for this snow type.
The results presented here are specific to one penetrometer tip shape and size, namely a rounded, 12 mm diameter tip. In order to generalize the deformation patterns to objects of an arbitrary shape and size, experiments similar to those described here will have to be repeated using a wide variety of penetrating objects.
Acknowledgements
We thank J. Johnson and an anonymous reviewer for providing many helpful suggestions that greatly improved the clarity of the manuscript. We thank D. Gauthier, L. Bakermans, C. Brown, A. Haeri, W. Rens, C. Campbell and M. Kolasinski for meticulous fieldwork observations. We thank Mike Wiegele Helicopter Skiing and Parks Canada for financial and logistical support specific to this project. We also acknowledge the support of the Natural Sciences and Engineering Research Council of Canada, the Canadian Avalanche Association, HeliCat Canada and Canada West Ski Areas Association.













