Introduction
Dynamic glacier processes contribute to climate change through several mechanisms including discharge of glacier ice into ocean waters. Changes in the dynamic parameters even of relatively small glaciers may have a disproportionately large impact on climate (Reference MeierMeier and others, 2007). Thus ongoing research efforts recognize that understanding and modeling the dynamics of mountain glaciers contributes a significant component to the validity of long-range climatological modeling (Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999).
Glacier dynamics are strongly tied to the basal conditions of glaciers (Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999; Reference Dow, Hubbard, Booth, Doyle, Gusmeroli and KulessaDow and others, 2013). For example, movement of hard-bedded glaciers depends largely on friction and shear forces at the ice/bedrock interface (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005). Water inputs at the bed of the glacier can cause glacier surging (Reference AndersonAnderson and others, 2004; Reference ClarkeClarke, 2005; Reference SmithSmith, 2007; Reference Howat, Tulaczyk, Waddington and BjörnssonHowat and others, 2008; Reference Magnússon, Björnsson and RottMagnússon and others, 2010), and the thickness of an existing water layer may be critical to estimating debris-bed friction (Reference Cohen, Iverson, Hooyer, Fischer, Jackson and MooreCohen and others, 2005). The presence of subglacial sediments may impact glacier movement through deformation, decoupling, sliding and uplift mechanisms (Reference Alley, Blankenship, Bentley and RooneyAlley and others, 1987; Reference Porter and MurrayPorter and Murray, 2001; Reference AnandakrishnanAnandakrishnan, 2003; Reference MacGregor, Riihimaki and AndersonMacGregor and others, 2005; Reference Evans, Phillips, Hiemstra and AutonEvans and others, 2006; Reference Hart, Rose and MartinezHart and others, 2011). In fact, interactions with basal sediments may be responsible for 80% or more of glacier movement in some cases (Reference Hart, Rose and MartinezHart and others, 2011).
In other cases, a distinct basal layer of debris-rich ice may exist (Reference HartHart, 1995). Increased rates of shear deformation or compression due to stratified facies and debris lenses within such a layer may cause >50% of overall glacier motion (Reference KnightKnight, 1997; Reference Hart and WallerHart and Waller, 1999; Reference Waller, Hart and KnightWaller and others, 2000; Reference Chandler, Waller and AdamChandler and others, 2005). Previous research has used a plethora of geophysical techniques, including both radar and seismic reflection methods, in attempts to define basal conditions and characterize these debris-rich basal ice layers where present (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986; Reference HartHart, 1995; Reference Baker, Strasser, Evenson, Lawson, Pyke and BiglBaker and others, 2003; Reference King, Woodward and SmithKing and others, 2004; Reference Brown, Harper and BradfordBrown and others, 2009; Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others, 2010; Reference Kim, Lee, Hong, Hong, Jin and ShonKim and others, 2010; Reference Bradford, Nichols, Harper and MeierbachtolBradford and others, 2013; Reference Dow, Hubbard, Booth, Doyle, Gusmeroli and KulessaDow and others, 2013).
Proper interpretation of seismic reflection data in particular can sometimes provide information about the physical properties of glacier ice and subglacial materials (Reference AnandakrishnanAnandakrishnan, 2003; Reference SmithSmith, 2007). However, resolution limitations may preclude the reliable detection of thin layers at the bed of glaciers, where ‘thin’ means less than half the dominant wavelength λ in the material of interest (Reference SmithSmith, 2007; Reference BoothBooth and others, 2012). Given the typical range for P-wave velocity α in subglacial materials (Table 1), at a central frequency of 250 Hz an 11 m thick basal ice layer (BIL) may still be considered seismically thin. (For additional discussion, see the classic article by Reference WidessWidess (1973).) Since these thin layers may dramatically impact glacier dynamics, quantifying their properties is essential (Reference Chandler, Waller and AdamChandler and others, 2005; Reference SmithSmith, 2007). Performing such quantification using seismic reflection methods can require the use of advanced techniques such as attribute analysis and inversion methodologies (Reference BoothBooth and others, 2012).
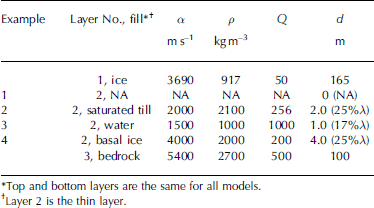
Table 1. Representative material properties in the glacier system*

Targeted full-waveform inversions (FWIs) incorporate all the information contained within a reflection event rather than parameterizing individual attributes (Reference Plessix, Baeten, De Maag, Ten Kroode and ZhangPlessix and others, 2012; Reference Babcock and BradfordBabcock and Bradford, in press). In general, FWIs invert for subsurface parameters by iteratively minimizing the difference between the observed data and a synthetic model with respect to subsurface parameters (Reference Plessix, Baeten, De Maag, Ten Kroode and ZhangPlessix and others, 2012; Reference OpertoOperto and others, 2013). FWIs thus have the potential to directly recover layer properties. However, FWI is complicated by problems of nonlinearity and solution non-uniqueness, the coupled nature of material properties, and computing speed (Reference OpertoOperto and others, 2013). Nevertheless, previous work has successfully applied a targeted FWI algorithm to quantify thin-layer properties using radar reflection data (Reference Babcock and BradfordBabcock and Bradford, in press). The targeted approach reduces the complexity of the inverse problem and minimizes computing time. Here we demonstrate the efficacy of the targeted FWI approach on synthetic seismic data. We then apply the inversion algorithm to a seismic dataset from Bench Glacier, Alaska, USA, in an attempt to quantify its basal conditions.
Theory And Application To Synthetic Testing
Forward algorithm
We use a one-dimensional (1-D), vertical-incidence reflectivity method to generate a reflection series from any given layered subsurface (Reference MüllerMüller, 1985; Reference Babcock and BradfordBabcock and Bradford, in press). This algorithm accounts for multiples and attenuation via the full wavenumber calculation. However, it assumes a vertical-incidence reflection in a system composed of linearly elastic, homogeneous layers and does not account for two- or three-dimensional (2- or 3-D) effects. Obviously the glacier environment can violate these assumptions to some extent since glacier ice is not homogeneous and the glacier bed may be irregular. Nevertheless, this 1-D approach provides a reasonable approximation for reproducing seismic reflection events where a thin layer is present and violations of the assumptions are not too severe. Reference Babcock and BradfordBabcock and Bradford (in press) detail the use of a similar forward algorithm for radar data. Here we present additional considerations and theory relevant to seismic methods.
Seismic velocities are frequency-dependent (Reference Aki and RichardsAki and Richards, 1980). We calculate the frequency-dependent velocity α’ as
where ω is frequency, Q is the seismic quality factor and α denotes the material’s reference velocity P-wave velocity at the central frequency ω 0 (Reference Aki and RichardsAki and Richards, 1980). The seismic quality is indicative of attenuation in a given medium; lower Q results in more rapid attenuation of the seismic energy. The seismic wavenumber k * is complex valued. Its real part is a function of α’ while the imaginary part is the attenuation component and depends on α’ and Q:
When seismic energy traveling through the subsurface encounters a contrast in material properties, some of the energy is reflected back to the surface. We use k * and density, ρ, to compute the acoustic reflection and transmission coefficients for upgoing and downgoing energy at an interface. We assume the waves impinge at normal incidence on planar, flat-lying layers composed of homogeneous linearly elastic materials separated by a welded interface. Our reflectivity method uses these coefficients to calculate the total reflectivity from the stack of layers (R 1) following Reference MüllerMüller (1985). The resulting reflectivity from the total stack mimics what we observe at the surface. Thus R 1 is the exact analytical response including multiples, scattering and transmission effects. We then convolve R 1 with a source spectrum and transform the result to the time domain with an inverse Fourier transform.
Inversion
The inversion algorithm uses a Nelder–Mead simplex search to minimize the objective function ϕ with respect to any set of parameters the user chooses from those constituting the forward algorithm (Reference Lagarias, Reeds, Wright and WrightLagarias and others, 1998; Reference Babcock and BradfordBabcock and Bradford, in press). The objective function minimizes the misfit between the data and the computed forward algorithm as
where d obs is the windowed data and d calc is the reflectivity response calculated using the 1-D forward algorithm discussed in the previous subsection. The data window is user-defined to incorporate the entire reflection event.
We use a Monte Carlo scheme to initialize starting values from a random distribution bounded by physically realistic limits for each parameter (Reference FishmanFishman, 1995). The inversion parameters may consist of any subset of the input parameters from the forward algorithm. In the 3-layer case, each layer has 4 parameters (α, Q, ρ and d) for a total of 12 parameters. We can invert for any subset of these parameters. The inversion algorithm then uses the gradient-based search around the user-defined parameters to find a local minimum (ϕ LM) for each iteration. We repeat the minimization routine 1000 times for each complete inversion and calculate the mean (x) for each parameter from the subset of global minima (ϕ GM).
We estimate uncertainty by evaluating Eqn (3) for 10 000 parameter pairs around the global minimum and then computing the root-mean-square error (RMSE) for those pairs. The subset of paired solutions that fit the data within a 5% noise level defines the solution. We report errors for the following solution pairs: α, ρ; α, Q; and α, d. While this method does provide an easily visualized estimate of uncertainty, note that the solution space is multidimensional and thus the 2-D uncertainty calculations do not entirely constrain the solution space. For example, the solution uncertainties for α and ρ may in fact be constrained by layer thickness. In that case, evaluating the 3-D solution space of α, ρ and d together would be necessary to define uncertainty.
Synthetic Demonstration
Synthetic testing: thin layers
We use the 1-D reflectivity algorithm to produce four synthetic seismic traces which serve as a basis for inversion testing. We add 5% random Gaussian noise to each trace before inversion. The traces simulate four different typical basal conditions: (1) glacier ice overlying bedrock; (2) a thin layer of sediment between the ice and bedrock; (3) a thin layer of water at the glacier bed; and (4) an underlying layer of frozen unconsolidated glacier debris (Fig. 1). The first trace acts as a control where the thin-layer thickness was set to 0 and thus the reflection event comes from the layer 1/layer 3 boundary. Table 2 gives parameters used in synthetic testing based on representative literature values from several sources including Reference Press and ClarkPress (1966), Reference Johansen, Digranes, Van Schaack and LønneJohansen and others (2003), Smith (2007), Reference BoothBooth and others (2012) and Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012). The thin-layer α, Q, ρ and d are the user-defined thin-layer inversion parameters. We also input the overburden thickness l as an inversion parameter but do not discuss those results as they are primarily a function of overburden velocity, which remains constant throughout these examples.

Fig. 1. Results for synthetic testing for four synthetic examples described in the text. Thin solid line is synthetic trace with 5% added Gaussian noise, and thick dashed line indicates inversion solution.
Table 2. Parameters for synthetic examples simulating a hard bed, a thin layer of basal till, water at the glacier bed, and a basal ice layer
Synthetic results: thin layers
Control
Although we generated the trace for the control case with d = 0 m, as with the other examples we inverted for layer properties as if a thin layer were present. The inversion algorithm returned d = 0.05 ± 0.05 m, layer α = 2400 ± 800 m s–1, Q = 1 ± 1 and ρ = 2200 ± 700 kg m–3 (Table 3). While solution α and ρ fall near acceptable values for glacial sediment (Table 1), solution d is negligible when compared to the wavelength (d = 1/200λ at α = 2500 m s–1). This solution d is likely the result of the inversion algorithm fitting some of the noise in the trace. Thus this inversion test confirms that the algorithm performs well in the synthetic case simulating no thin layer present at the bed.
Table 3. Thin-layer parameters for synthetic testing and the inversion mean for thin-layer parameters calculated from all results for ϕ GM

For the control, examination of parameter pairs did not produce any meaningful assessment of solution uncertainty. This problem could arise when parameter coupling is too complicated to be resolved with 2-D solution appraisal. Therefore here we estimated solution uncertainty from the subset of the 1000 inversion iterations where ϕ LM was within 5% of ϕ GM. This method for estimating solution uncertainty gives similar constraints on the inversion solution for the synthetic control to those for the other synthetic examples (Table 3).
Examples 2, 3 and 4
Inversion results for thin-layer parameters are within 5% of the true values for the remaining synthetic examples, with the exception of solution d for the thin water layer and of solution Q (Table 3; Fig. 1). Error in solution d for the thin water layer is 10%. All solution Q values appear unreasonable. Estimated solution uncertainty for both α and ρ is large in some cases, with estimated coefficient of variations (cv) ranging from 5% to a high of 25% for the frozen unconsolidated layer (Table 3). On the other hand, uncertainty estimates for Q are unreasonably low (cv < 3%). This cv is likely not a reliable representation of Q uncertainty, especially given the fact that Q results are well outside the defined parameters.
Synthetic testing: layer thickness
In order to test the sensitivity of the inversion algorithm to layer thickness, we generate six additional synthetic traces simulating a basal sediment layer with thin-layer thickness from 0.2 m (0.025) to 4 m (0.5) thick. For this test we hold other parameters constant having values as shown in Table 3 and define d as the sole inversion parameter. We estimate 1-D solution uncertainty as described previously for source Q inversion uncertainty estimates.
Synthetic results: layer thickness
Figure 2 shows synthetic traces and bounded solutions for six different test cases of sediment thickness. Table 4 reports associated uncertainties and cv for each result. In this case the inversion performs remarkably well even when d = 0.025, and all inversion solutions are within 5% of the true value. In all cases the inversion solution underestimates thin-layer thickness. Estimated uncertainty increases (cvmax > 50%) as d decreases.

Fig. 2. Results for parameter sensitivity testing for synthetic example with varying layer thickness. (a) The six traces, with increasing layer thickness from left to right. Thin solid line is synthetic trace with 5% added Gaussian noise, and thicker dashed line indicates inversion solution. All traces are normalized by the maximum source amplitude. (b) Inversion solution for solution d versus true d and estimated solution uncertainties. Uncertainties for lower layer thicknesses are 25 times greater than the uncertainty associated with the thickest layer which is not evident in the plot (see Table 4).
Table 4. Results for parameter sensitivity testing for six synthetic tests with increasing d. Uncertainty associated with smallest value for d is >25 times greater than for the thickest layer tested

Summary of synthetic results
The inversion solution for layer parameters except Q during synthetic testing was within 5% of true values for the four synthetic traces with the exception of the erroneously low value for the thickness of the thin water layer. In the control example, solution d is extremely small (±0.05 m), and it is obvious that in reality the thin layer is absent (Table 3; Fig. 1). For examples 2, 3 and 4, other than solution Q the estimated parameter uncertainties encompass the true synthetic values. Associated uncertainties for several layer properties were high, notably in the case of ρ and α for the thin water layer (cv 30%) and thin frozen layer (cv 25%). This result highlights the problem of non-uniqueness inherent in implementation of FWIs. However, since the solution space is four-dimensional, absolute estimation of uncertainty requires 4-D analysis of the solution space which we have not attempted.
On the other hand, solution Q is inaccurate for all synthetic testing. For examples 2 and 3, solution Q is >200% of the true Q; and associated uncertainties for Q are unreasonably low. For example 4, solution Q is 15% of the true value. Thus the synthetic testing demonstrates that the inversion algorithm is not sensitive to layer Q for these layers and layer thicknesses and that reasonable constraints on Q values for the bounded inversion may be necessary in order to produce physically meaningful inversion results. Holding Q fixed during the inversion may prove a better option since using fewer inversion parameters will increase inversion speed. Overall, the preceding synthetic results demonstrate both the functionality and also the limitations inherent in this FWI algorithm. They show that we can reasonably expect that this inversion algorithm can recover the basal properties of a glacier in the presence of a thin layer.
Application To Bench Glacier
Field site
Bench Glacier is a temperate glacier located near Valdez, Alaska, in the coastal Chugach mountain range (Fig. 3). Bench Glacier is ~7 km long and ~1 km wide. Ice thickness in the survey location ranges from 150 to 185 m (Reference Riihimaki, Gregor, Anderson, Anderson and LosoRiihimaki and others, 2005; Reference Brown, Harper and BradfordBrown and others, 2009). The glacier’s convenient location and moderate slope (<10°) have made it a conducive field site for multiple campaigns (e.g. Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999; Reference MacGregor, Riihimaki and AndersonMacGregor and others, 2005; Reference Riihimaki, Gregor, Anderson, Anderson and LosoRiihimaki and others, 2005; Reference Fudge, Humphrey, Harper and PfefferFudge and others, 2008; Reference Meierbachtol, Harper, Humphrey, Shaha and BradfordMeierbachtol and others, 2008; Reference Brown, Harper and BradfordBrown and others, 2009; Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others, 2010; Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others, 2012; Reference Bradford, Nichols, Harper and MeierbachtolBradford and others, 2013).

Fig. 3. (a) Bench Glacier, showing location of 3-D seismic survey (white shading) and surface seismic monitoring station locations (+) where Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012) report surface ice velocities and Q values; 20 m contours show bed elevation. Black line intersecting 3-D survey area is location of 2-D seismic profile shown in Figure 4c. (b) 3-D survey map with grayscale fold density (lighter shade indicates higher fold) showing trace locations for inversion within the box in area of highest fold; arrows point to white boxes enclosing receiver locations, and * indicates source locations. Marked x and y directions on plot correspond to those in Figures 6 and 7, with x 0, y 0 at lower left corner of inversion box.
The lithology of Bench Glacier bedrock is characterized by meta-greywacke, which is dominated by quartz and feldspars (Reference Winkler, Silberman, Grantz, Miller and KevettWinkler and others, 1981; Reference BurnsBurns and others, 1991). Representative seismic attributes for this bedrock include α = 5400–6300 m s–1, ρ = 2.68–2.71 kg m–3 and Q = 200–1500 (Reference Press and ClarkPress, 1966; Reference FowlerFowler, 1990). P-wave velocities reported for Bench Glacier range from 3630 to 3780 m s–1 (Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others, 2012; Reference Bradford, Nichols, Harper and MeierbachtolBradford and others, 2013). Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012) report mean overburden ice Q = 42 ± 28 from Rayleigh waves at a central frequency (f 0) of 45 Hz. We assume bulk glacier density to be 917 kg m–3 (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999). The consistent P-wave velocities and reasonably flat bed topography in the region of our survey (Fig. 4) lend credence to the use of our 1-D forward algorithm in light of its inherent limitations which we previously mentioned.

Fig. 4. Data from Bench Glacier. (a) Time-migrated 2-D seismic profile across the survey area (solid line in (b, c)). Note change in reflection characteristics across the length of the bed: arrows on left point to the peaks of two reflection events marked by dashed lines that converge across the glacier. At ice velocity, the maximum peak-to-peak distance closest to our survey is 8 m, or ~55%, and black line denotes this region. (b, c) Two representative super-gathers with binned offsets and Rayleigh wave muting. For viewing purposes these data have automatic gain applied with a 50 ms sliding window. Vertical line marks the offset range (80 m) used for trace stacking prior to inversion input.
Previous seismic surveys have uncovered the possible presence of a discontinuous basal layer beneath Bench Glacier (Reference Bradford, Nichols, Mikesell, Harper and HumphreyBradford and others, 2008). A 2-D seismic profile collected in 2007 highlights the presence of a layer that thins in the cross-glacier direction (Fig. 4; Reference Bradford, Nichols, Mikesell, Harper and HumphreyBradford and others, 2008). The reflection profile demonstrates an additional reflection separating from the bed arrival beginning around 175 m of the survey distance. This layer pinches out around 350 m, indicating the presence of a discontinuous or thinning basal layer. Previous researchers have conjectured that the glacier may be hard-bedded or have discontinuous sediment present at the bed ranging from 1 to 2 m thick (Reference MacGregor, Riihimaki and AndersonMacGregor and others, 2005; Reference Fudge, Harper, Humphrey and PfefferFudge and others, 2009). It is also possible that there is a layer of debris-rich basal ice, similar to other glaciers in this region (Reference HartHart, 1995). With that in mind, we apply the FWI to a discrete set of data co-located with the 2-D survey to determine what material could comprise this basal layer.
Data collection and preparation
We conducted a seismic survey in summer 2007 using an 8 kg manually operated jackhammer fitted with a flat plate as the seismic source in a 10 m × 10 m shot grid over a 300 m × 300 m surface area (Fig. 3). The resulting 3-D P-wave seismic reflection profile had a checkerboard receiver pattern (40 Hz vertical geophones) in four 5 m × 5 m grids. The nominal common-midpoint (CMP) bin size is 2.5 m, and survey geometry produced a maximum of 50–70 reflection samples from the ice/bed interface at different offsets within each of these bins (Fig. 3). Maximum offset was 384 m. The lack of snow or firn cover at the glacier surface during the data collection period allowed for effective source coupling but also caused some receiver coupling problems as receiver locations melted out of the ice over the course of a day of data collection and had to be reset.
Basic processing steps include removing unusable traces due to receiver meltout or other problems, muting the Rayleigh wave, employing elevation statics, applying a bandpass filter (50–100–400–600 Hz) and applying a geometric spreading correction (t1). To further reduce noise, after velocity analysis we combined and stacked offsets in 5 m increments for offsets less than 80 m. Constraining offsets to this range limits stretch effects in velocity processing and reduces problems associated with the azimuthal anisotropy known to exist in this glacier ice.
Following Reference Bradford, Nichols, Harper and MeierbachtolBradford and others (2013), in the area of greatest fold we created 3-D supergathers by combining 3 × 3 groups of binned CMPs. Figure 4 shows representative supergathers. Then we selected 25 supergather formations in the area of greatest fold (Fig. 3). Based on bin size, geometry and estimations of the size of the Fresnel zone, these traces cover about 62 m × 62 m, or ~4000 m2 which is ~0.05% of the total glacial area. In this small area the basal geometry is relatively flat. As previously stated, we limit incidence angles to those below 15° so that the normal incidence assumption of the forward algorithm is valid and to minimize effects associated with azimuthal anisotropy. After velocity correction using α = 3690 m s–1, we stack the traces within each supergather. The result is a single trace per supergather formation simulating a zero-offset seismic reflection event. We implement the inversion on each of the 25 traces after target windowing around the basal reflection event following Reference Babcock and BradfordBabcock and Bradford (in press).
A key step to implementing any FWI algorithm is accurately characterizing the effective source wavelet (Reference Plessix, Baeten, De Maag, Ten Kroode and ZhangPlessix and others, 2012; Reference OpertoOperto and others, 2013). With that in mind, we begin by delineating steps to recover the effective source parameters from the direct arrivals in the seismic data collected at Bench Glacier. Finally, we implement the inversion algorithm on the field data collected at Bench Glacier to quantify its basal properties.
Source recovery
Before we can test the inversion algorithm on either synthetic or field seismic data, we must accurately recover the source parameters. We use the direct arrivals from the seismic dataset to derive the effective source parameters as follows. Visual examination of the data and comparison with results from Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012) reveals that the direct P-wave arrivals are well separated from the Rayleigh wave after ~50 m of offset. Therefore we select offsets ranging from 50 to 75 m from which to extract the source wavelet characteristics. After the basic processing steps previously defined, we apply a linear moveout (LMO) correction at an average velocity of 3640 m s–1. Although lower than the bulk ice velocity, this velocity proved effective at flattening the direct arrivals. Surface velocity could be lower than bulk velocity due to a higher fracture concentration of crevasses and other heterogeneities near the surface. Finally, we stacked all traces within each offset bin to produce a single representative trace containing the direct P-wave arrival for a given offset, resulting in five traces which each represent a distinct offset (Fig. 5).
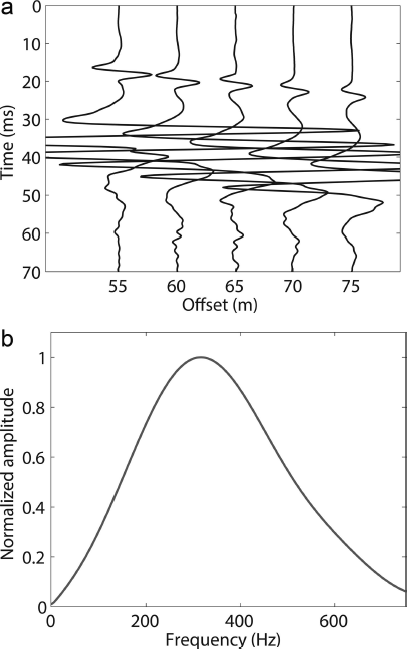
Fig. 5. (a) Seismic record for stacked traces binned between 55 and 75 m offset. Straight solid line underscores direct arrivals, and arrow points to Rayleigh waves. (b) Extracted source wavelet spectrum.
Next, after correcting for spherical divergence we invert for seismic Q using a version of the primary gradient-based search algorithm. In this case the objective function ϕ minimizes the differences between the five traces after back-propagation and attenuation (Q) correction as follows:
where P is a matrix of five column vectors each composed of one back-propagated and attenuation-corrected waveform Pi, i denotes a column of P, and j denotes the row-wise sum of the matrix R formed from P. We calculate the back-propagated and attenuation-corrected waveform Pi for each of the five source wavelets (Si ) using the Fourier transform of the direct arrivals shown in Figure 3:
Thus this technique inverts for the seismic attenuation factor by using Eqn (5) to minimize Eqn (4) with respect to Q. We calculate the solution uncertainty for the single inversion parameter as those Q values having RMSE ±5%.
The source parameter inversion returns Q = 26 ± 6. The result is within the range of Bench Glacier surface Q values calculated by Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012) but 40% lower than their average value. However, their survey is located slightly up-glacier of our data collection region (Fig. 3). In addition, Reference Mikesell, Van Wijk, Haney, Bradford, Marshall and HarperMikesell and others (2012) used low-frequency Rayleigh waves rather than the high-frequency P-wave direct arrivals, so the representative volume of their Q measurement includes deeper ice than the surface waves. Surface ice Q should be lower than bulk Q since attenuation is likely to be greater near the surface due to scattering caused by surface topography and air-filled crevasses. Furthermore, ice Q is known to vary widely in response to ice conditions and temperature. For example, Reference Gusmeroli, Clark, Murray, Booth, Kulessa and BarrettGusmeroli and others (2010) report a range for Q from 6 to 175 for temperate ice. With these considerations defending the reasonableness of our inversion Q result, we apply this Q to all five traces after spherical divergence correction and take the mean spectrum of the result. That spectrum provides the source spectrum for the 1-D reflectivity algorithm (Fig. 5).
Results
User-defined inversion parameters are α, ρ, d, overburden thickness and overburden Q. We invert for overburden Q instead of layer Q for three reasons: (1) the impact of overburden Q on wavelet attenuation is greater than that of layer Q since the wave’s travel path in the ice is >300 m as compared to an estimated maximum thin-layer travel path of 4 m (Reference Fudge, Harper, Humphrey and PfefferFudge and others, 2009); (2) effective overburden Q is not well known, as robust estimates for Q on Bench Glacier are surface-derived measurements and do not reflect bulk Q over the ice volume which our inversion traces sample; and (3) synthetic testing demonstrated inversion insensitivity to thin-layer Q. Overburden thickness also functions as an inversion parameter. We do not discuss these results here for two reasons: (1) they are trivial as they agree well with the radar-derived ice measurements; and (2) our primary goal is to recover the thin-layer parameters rather than the over-burden thickness. We use the source spectrum derived from the direct arrivals for the source in the 1-D reflectivity algorithm as described previously (Fig. 5).
Mean results for the inversion parameters over the whole inversion area (box, Fig. 3b) are α = 4000 ± 700 m s–1, ρ = 1900 ± 200 kg m–3, d = 6 ± 1.5 m and overburden Q = 68 ± 21 (Table 5). We refer to these values as the total solution. For visualization purposes, Figure 6 shows five traces and the corresponding inversion solutions. Total ranges for the 25 inversion solutions are 3200–4700 m s–1 for α, 1700–2400 kg m–3 for ρ, 2–9 m for d, and 50–100 for overburden Q (Table 5; Fig. 7). Out of the 25 solutions, 3 have d < 5 m, 2 have d > 7 m and the remaining solution d fall within 5–7 m. Similarly, if we exclude 2 solutions having ρ 2400 kg m–3, the total range of solutions for ρ becomes 1700–2100 kg m–3. Excepting two high and low values noted in Table 5, solution α ranges from 3500 to 4200 m s–1. The range of solutions for Q exhibits more variability than the other three parameters, with up to 100% variations in Q, depending on trace location (Fig. 7). We calculate the paired parameter uncertainties as described previously for the 4 parameters for 5 of the 23 solutions. The total uncertainty for the mean solutions reported in Table 5 results from the average cv for each variable from these 5 paired solution uncertainties applied to the mean of the solutions. Figure 8 shows the complicated nature of the paired uncertainties, especially for solution Q.
Table 5. Solution range and total mean solution with estimated uncertainty and inversion bounds for 25 field data traces
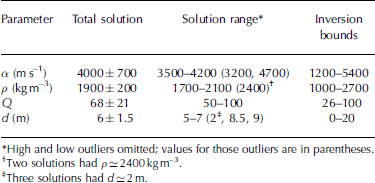
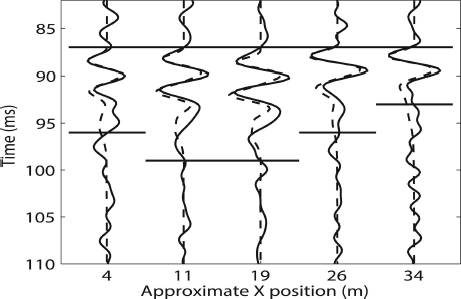
Fig. 6. Five representative supergather traces (solid line) and the inversion solution (dashed line) taken from approximately y = 4 m and x positions across the lower portion of the inversion box shown in Figure 3b. Horizontal solid lines define target window for each trace, and all traces are normalized by the maximum source amplitude. Target window choice depends on user discretion and is an essential consideration in the inversion process.
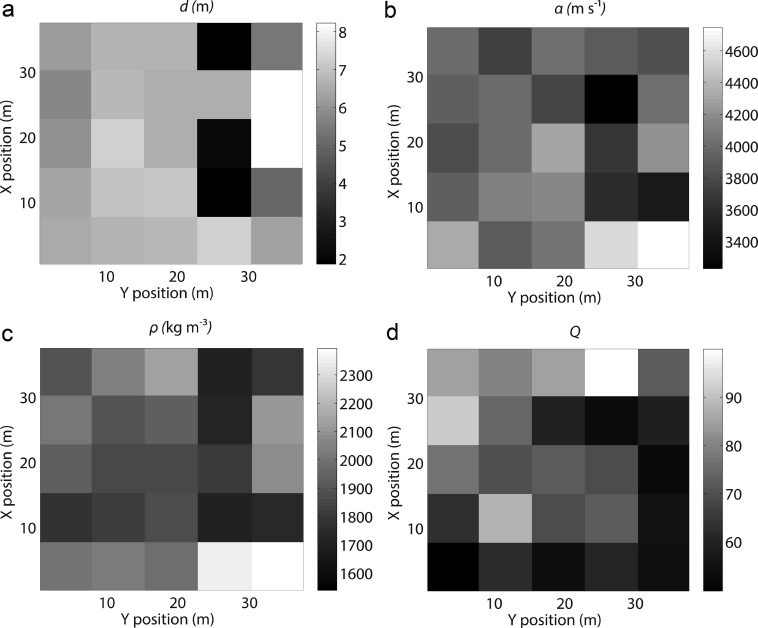
Fig. 7. Solutions for 25 supergathers for (a) layer d (m); (b) α (m s–1); (c) ρ (kg m–3); and (d) overburden Q. Note scales for each plot, where x, y positions are relative to inversion box shown in Figure 3b starting at lower left corner. Mean estimated uncertainties are reported in Table 5. Each box represents the inversion solution for the appropriate variable from one stacked supergather.
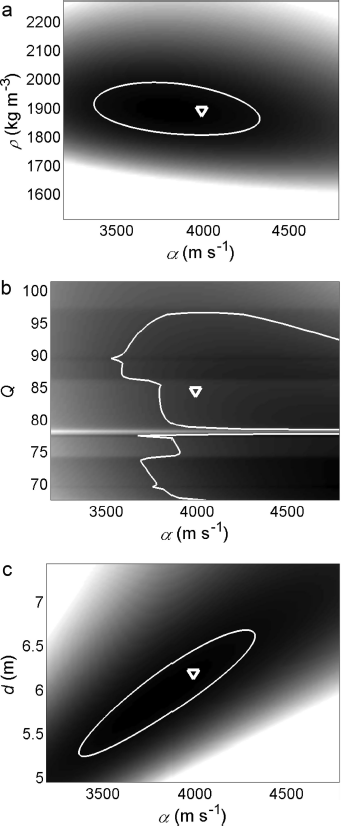
Fig. 8. Demonstration of paired parameter solution uncertainty plots for one reference inversion solution for (a) α (m s–1) vs ρ (kg m–3); (b) α vs Q; and (c) α vs d (m). Darker colors correspond to lower uncertainties, and scale is relative to each parameter pair. White line encloses solutions from the parameter pair with RMSE ±5%, and triangle marks the inversion solution. In general, other uncertainty plots show similar characteristics. Here α, Q pairs (b) demonstrate the possibilities of multiple local minima with the concurrent difficulties such a situation poses for ill-constrained FWI problems.
Discussion
The total inversion solution for α (4000 ± 700 m s–1) is within published ranges for debris-rich basal ice layers (BILs) or frozen sediment layers (e.g. 2300–5700 m s–1) (Table 1; Fig. 7) (Reference McGinnis, Nakao and ClarkMcGinnis and others, 1973; Reference Johansen, Digranes, Van Schaack and LønneJohansen and others, 2003). The total slowness or velocity inverse (s (s m–1)) of the composite material is approximately the sum of the fraction f of each component times the slowness (Reference Hauck, Böttcher and MaurerHauck and others, 2011):
where the subscripts BIL, i, r, a and w denote basal ice layer, bulk ice, rock, air and water respectively. We assume that the water content of the BIL is negligible since Reference Bradford, Nichols, Harper and MeierbachtolBradford and others (2013) determined the bulk volumetric water content of Bench Glacier in our survey area to be <1%. We further assume that there is no void space in the BIL, i.e. f a = 0. With these two simplifications, Eqn (6) reduces to a two-component mixing equation for slowness:
where f i = 1– f r. We can simplify and solve Eqn (7) for the rock fraction as follows:
The corresponding slowness s BIL = 2.5 × 10–4 s m–1 to the mean inversion velocity yields a rock fraction of 30%. Excluding outliers, the highest seismic velocity from the inversion is 4200 m s–1 (Table 5). This velocity corresponds to a rock fraction of 43%. Equation (8) fails where reported layer seismic velocities are less than ice velocity (α ice) (i.e. layer slowness s BIL > s i). Solution α for 2 of the 25 inversion traces was below α ice.
However, Eqn (8) does not take into account the geometry or distribution of the rock inclusions. Another source of error is our assumption that there is no free water in the BIL. Reference Harper, Bradford, Humphrey and MeierbachtolHarper and others (2010) show that water-filled basal crevasses are present on Bench Glacier. These observations combined with the timing of the data collection (August) suggest that water in liquid form is present throughout the glacier crevasse system. It is possible that BIL volumetric water content is as high as 2.5% (Reference Bradford, Nichols, Mikesell and HarperBradford and others, 2009). Using the three-phase approximation to Eqn (6) with f w = 2.5% and f i = 70%, the BIL bulk seismic velocity may be as low as 3700 m s–1 (Fig. 7). This value is well within the uncertainty of the mean solution.
The total inversion solution for ρ is 1900 ± 200 kg m–3, with the solution ranging from 1700 to 2000 kg m–3 excluding one outlier (Table 5). We use a common mixing equation to interpret these results with respect to rock fraction for the two-phase system (Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999):
where ρ BIL is the density of the BIL. Solving for f r, the resulting rock fractions for the inversion results range from 40% to 65%. These values are within published ranges for debris concentrations of debris-rich BIL layers (30–59%) (Reference HartHart, 1995; Reference Hart and WallerHart and Waller, 1999). In addition, the robustness of the inversion solution is further corroborated by the consistency of the rock fraction results from analysis of both α and ρ. Combined interpretation of the analysis for inversion solutions for α and ρ suggests that there is indeed a thin layer of debris-rich basal ice present below the glacier at this location. Given the range of solution ρ, this BIL likely has relatively high concentrations of debris (40–65%). An alternative interpretation could be the presence of basal layers of saturated, frozen sediments with high porosity. However, such layers are not likely to form beneath a temperate glacier such as this one.
The 2-D seismic profile previously collected at our survey location corroborates our findings (Fig. 4). Based on peak-to-peak time difference between arrivals of the thinning basal layer observed in the stacked data, the thickness of this layer nearest our survey area is ~8 m. The inversion result for d (6 ± 1.5 m) corresponds roughly to the center of the section where visual examination shows the basal layer is thinning out.
Next we interpret our results for overburden Q (Q = 68 ± 21). Overall the inversion solution for Q falls well within reported literature values (e.g. Reference Gusmeroli, Clark, Murray, Booth, Kulessa and BarrettGusmeroli and others, 2010). Furthermore, our surface wave inversion, the synthetic inversion results and the bulk Q inversion results all demonstrated that the inversion algorithm is not strongly sensitive to Q for these high Q values. To test that observation, we reran the inversion for the entire set of 25 traces with Q fixed and equal to the inversion mean solution (Q = 68). The resulting mean inversion solutions deviated <5% from the solutions in Table 5, and the average run time was half the run time when including Q as an inversion parameter. Thus we conclude that fixing Q to a reasonable value based on some knowledge of overburden conditions has minimal impact on inversion accuracy and may prove a reasonable approach, especially given the complicated nature of the Q solution which may trap the inversion in discrete local minima (Fig. 8).
Finally, it is important to note that target window length is an inversion input based on user discretion. Figure 6 shows the window lengths in the inversion for five field data traces. The window length varies in order to ensure inclusion of all data due to the basal reflection; a longer window is necessary where the reflection contains multiple peaks. Reference Babcock and BradfordBabcock and Bradford (in press) noted that a shorter window length may provide a more accurate inversion result than a longer one. Thus it seems that the higher-amplitude parts of the reflection event contain most of the information and are least sensitive to noise. We attempt to define window length so as to include the entire reflection event but exclude noise (Fig. 6). Target window remains based on practitioner judgment; future work should include a more robust assessment of ideal target window.
Conclusions
We applied a FWI algorithm to synthetic seismic data and to field data taken from Bench Glacier in an effort to quantify thin-layer parameters for basal layers. The inversion implements a gradient-based search algorithm in conjunction with a 1-D vertical incidence reflectivity algorithm. During testing on four synthetic examples with 5% added random Gaussian noise, the inversion recovered thin-layer parameters within 10% of true values. Additionally we tested the inversion on six different thin-layer thicknesses from 0.025λ to 0.5λ. Inversion results for these tests were within 5% of true values. Finally, the FWI algorithm recovers mean α = 4000 ± 700 m s–1, ρ = 1900 ± 200 kg m–3 and d = 6 ± 1.5 m using a subset of field data collected during a glacier seismic survey. We interpret these results to be indications of the presence of a debris-rich basal ice layer at the sample locations.
However, the inversion procedure has many steps including choosing target window, choosing whether to invert for Q, determining paired parameter uncertainties where possible, and inverting for ice thickness. Thus future work includes quantification of inversion sensitivity to seismic Q, investigation of the effects of window length on solution robustness, and implementation on additional datasets where boreholes have been more effective at establishing basal conditions. With such additional work, future judicious implementation of this algorithm could quantify properties of thin layers under glaciers and ice sheets. Such accurate quantification of basal parameters will aid interpretation and modeling of glacier and ice-sheet dynamics in response to climate change.















