Position of Ice Divides and Ice Centers on Ice Sheets

Abstract

Model calculations are made of the magnitude of the shift of the portion of an ice divide on a two dimensional ice sheet and of the “center” (the position of highest elevation) of a circular ice sheet when the rate of accumulation is different on different sides or in different sectors of an ice sheet. It is concluded that gross changes in the accumulation pattern are required to cause an appreciable shift of the position of ice divides or ice centers if the positions of the edge of the ice sheet are fixed.

On a créé un modèle mathématique pour calculer l’importance de la variation de la position de la ligne de partage des pentes dans une calotte de glace à deux dimensions et du centre (le point le plus élevé en altitude) d’une calotte circulaire lorsque le taux d’accumulation est différent sur divers versants ou dans différents secteurs d’une calotte glaciaire. On en conclut que si les positions des limites extérieures de la calotte sont fixées, il faut de gros changements dans le mode d’alimentation pour entraîner un déplacement appréciable de la ligne de crête ou du centre de la calotte.

Zusammenfassung

Es wurden Modellrechnungen für das Ausmass der Verlagerung einer Eisscheide in einem zweidimensionalen Eisschild und des “Zentrums” (Ort der höchsten Erhebung) eines kreisförmigen Eisschildes angestellt, wenn die Akkumulationsrate auf den beiden Seiten oder in verschiedenen Sektoren eines Eisschildes verschieden ist. Sie führen zu dem Schluss, dass erst erhebliche Änderungen in der Akkumulationsverteilung eine merkliche Verlagerung der Eisscheiden oder -zentren verursachen, wenn die Ränder des Eisschildes in fester Position bleiben.

Introduction

The amount of information about past climatic conditions that can be extracted from deep drill-hole ice cores from the Greenland and the Antarctic ice sheets depends upon how well the past flow of ice of these ice sheets can be determined. The ultimate goal of this area of research is to know for any piece of ice taken from a drill hole: (1) its age, (2) its temperature when it was deposited upon the ice sheet, (3) the elevation of the ice sheet where it was deposited, and (4) the accumulation rate at the time it was deposited. The analysis of the past ice flow that is required to obtain all or part of this information is done most simply for ice underneath the center of an ice dome or the highest point of an ice divide on an ice sheet. At these sites the direction of ice motion is only in the vertical direction. Complications introduced into the analysis by the account that must be taken of whether or not sliding occurs at the base of an ice sheet and of the amount of horizontal movement of ice are greatly reduced. However, the positions of ice centers and divides in the past may not be close to where they are today. And if they are not, the simplicity of the analysis of ice flow for these unique places on an ice sheet is lost.

It appears important therefore to make an estimate, if it is at all possible to do so, of how much the positions of ice divides and ice dome centers on the Greenland and the Antarctic ice sheets might have shifted under changes in the conditions of accumulation. If the amount of shift in the position of the ice divide sites is relatively small for relatively large changes of accumulation patterns, errors that are introduced in the determination of quantities such as the age of the ice by the assumption that the position of an ice divide does not change with time probably are not very large.

Theory

Consider the cross-section of the two-dimensional ice sheet that is shown in Figure 1. The ice sheet is not necessarily symmetric. Therefore, let the subscripts r and l identify quantities from the right-hand and left-hand side of this ice sheet; let the origin of the horizontal axis be placed directly under the ice divide; let x _r and x ₁ represent horizontal distance measured from the origin in the right-hand and left-hand directions respectively; and let h _i , α _i , L _i ,and a _i , where i = r or l, represent the ice thickness, the slope of the upper ice surface (considered always to be a positive quantity), the width (distance from the origin to the edge of the ice sheet), and the accumulation rate, respectively (see Fig. 1).

Fig. 1. Cross-section of a two-dimensional ice sheet.

At the center of the ice sheet the ice thickness terms must satisfy the relationship

(1)

and at the edges the relationship

(2)

Under steady-state conditions, a simple mass-balance argument produces the equation

(3)

where u _i (xi) is the average velocity of ice in the horizontal direction at the distance x _i . (It is assumed that the amount of melting or freezing of ice at the bottom surface of the ice sheet is negligible compared with the term a _i .)

The average velocity u _i is given by

(4)

where C, m and n are constants. (See the texts of Paterson, 1969, or Lliboutry, 1964–65, for derivations of Equation (4) and calculations of ice-sheet profiles.) If the ice sheet does not slide over its bed the power n is the same as the exponent appearing in the power-law creep of ice and thus n ≈ 3. The constant m is equal to n+1 if the temperature and the anisotropy of ice do not vary with depth. This constant is approximately equal to n if the ice deformation is concentrated to an unusual extent near the bottom of the ice sheet because the temperature is much warmer there or because the ice is strongly oriented for easy glide there. If the ice sheet slides over its bed, and if most of the ice motion is produced by this sliding motion, n = m = (n ^*+1)/2 ≈ 2, where n ^* ≈ 3 is the power-law exponent of creep, if the sliding velocity is given by the equation (see Paterson, 1969) we have derived. (It is unlikely that sliding accounts for more than one-half of the total ice motion of a non-surging ice sheet.)

If Equation (4) is inserted into Equation (3) the following equation is found:

(5)

The solution of this equation, subject to the conditions given by Equations (1) and (2), is the profile of the ice sheet. If the bottom surface of the ice sheet is flat, α _i = −dh _i /dx _i ; if the bottom surface was flat before the ice sheet existed but then became curved as the result of the isostatic sinking produced by the weight of the ice, α _i = −γ dh _i /dx _i , where γ is a constant approximately equal to (Weertman, 1961). For either of these situations Equation (5) becomes

(6)

where K = C ⁻² for a flat bed and K = γ ⁻ⁿ C ⁻¹ for a shaped bed.

If Equation (6) is integrated and the constants of integration are chosen to satisfy the conditions given by Equations (1) and (2), the following relationship is found:

(7)

Equation (7) determines the position of the ice divide. If a _r(x _r) = a ₁(x ₁) for all values of x _r = x ₁ then obviously L _r = L ₁ and the ice divide is at the center of the ice sheet.

The position of the edges of the East Antarctic and Greenland ice sheets is essentially fixed by the deep seas around the land masses upon which they rest. Only the north-west corner of the Greenland ice sheet can shift, across a narrow channel into Ellesmere Island in Canada, to any marked extent. (Of course if large ablation areas were to develop on these ice sheets their edges could shift into the interior away from the coasts. We are concerned, however, in this paper with the situation in which 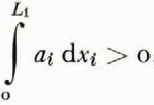. Thus the ice sheets must extend to the sea and discharge the excess accumulation as icebergs.)

If Figure 1 represents, say, an east-west cross-section of the Greenland ice sheet the sum of the widths L _r+L ₁ must be approximately equal to a constant. This constant is

(8)

where L is the width of a symmetric ice sheet. Let ∆L be the difference between the positions of the ice divides of a symmetric and a non-symmetric ice sheet. Thus

(9)

Constant Accumulation Rate

Equation (7) has a simple solution when the accumulation rates a _r and a ₁ are constant in value but not necessarily equal to each other. The solution is

(10)

where ∆a = a ₁−a _r and it is assumed that a ₁⩾ a _r. For small values of ∆a/a _r. Equation (10) reduces to

(11)

Figure 2 shows a plot of ∆L/L versus ∆a/a _r for the case of n = 3. (The side of the ice sheet with the heavier rate of accumulation has the smaller width.)

Fig. 2. Plot of ∆L/L versus ∆a/a_r and ∆c/c_r.

Very large differences between a ₁ and a _r are required to change the ice divide position appreciably from the symmetric position. For example, if a ₁ = 2a _r (or ∆a/a _r = 1) the value of ∆L/L is equal to only 0.086. Thus in south Greenland, where L ≈ 400 km, the shift in the position of the ice divide that would occur by increasing a ₁ by a factor of 2 is only 34 km.

Linearly Increasing Accumulation Rate

Suppose that the accumulation rate increases linearly with distance from the ice divide. (The accumulation rates in both Antarctica and Greenland, in general, are larger nearer the edges of these ice sheets than deep in the interior.) Let the accumulation rate be represented by the equation

(12)

If Equation (12) is inserted into Equation (7), the following equation for L _r and L ₁ is found:

(13)

Where Z _i = c _i L _i /2b _i and z is used as a dummy variable of integration.

When Z _i ⪡1, Equation (13) reduces to Equation (10). When Z _i ⪢ 1 Equation (13) reduces to

(14)

where ∆c = c ₁—c _r; it is assumed that c ₁ ⩾ c _r ⩾ 0. For small values of ∆c/c _r Equation (14) becomes

(15)

Figure 2 shows a plot of ∆L/L versus ∆c/c _r calculated from Equation (14) with n = 3. The magnitude of ∆L/L is somewhat smaller than that obtained from Equation (10) for identical values of ∆a/a _r and ∆c/c _r.

The spatial variation of the accumulation rate on an actual ice sheet will differ somewhat from the two simple analytical expressions used to obtain the curves shown in Figure 2. These curves are useful nevertheless to estimate the magnitude of the shift of the position of the ice divide when the average value of the accumulation rate on either side of the divide changes because of a change in the climate. We can conclude from the results presented in Figure 2 that very gross changes (a factor of three or more) in the ratio of the accumulation rates on either side of the ice divide must occur before the position of the ice divide is shifted over significant distances.

Asymmetric Ice Profile Produced by Asymmetric Bottom Topography

Even if the accumulation rate pattern is symmetric on either side of the ice divide of a two dimensional ice sheet, the ice sheet need not be symmetric in shape. If the topography of the bottom is uneven, and in general it will be, the ice sheet profile will not be symmetric. Figure 3 shows schematically an ice sheet resting on a bed whose right-hand side is higher than its left-hand side by a constant amount ∆h. The position of the ice divide of this ice sheet can be calculated from the equations of the previous sections provided that the following equation is substituted for Equation (1)

(16)

Fig. 3. Cross-section of two-dimensional ice sheet whose bed is higher on one side than the other.

The following equation is found for ∆L/L:

(17)

where h is the thickness of ice at the center of the ice sheet. (The side of the ice sheet with the higher bed has the larger width.)

If one side of an ice sheet can slide over its bed and the other side cannot, the ice sheet will be asymmetric even though both the bed topograph and the accumulation rate pattern are symmetric. The values of K, m, and n given in the previous section will differ for the two sides of the ice sheet. If the accumulation rate is a constant over both sides of the ice sheet, the value of ∆L/L is given by

(18a)

With the approximation that n _r = n ₁ = n and m _r = m ₁ and the assumption that a _r = a ₁ this equation reduces to

(18b)

Here m ₁, K _r, etc., refer to the values of m, K, etc., on the right- and left-hand side of the ice sheet, and h is the thickness of the ice at the center of the sheet. (The side of the ice sheet which flows more readily has the larger width.) Should sliding occur on only one side of an ice sheet the value of ∆L/L will be no longer than ≈ 0.1 because the ice velocity normally can vary by no more than a factor of about 2. Only if surge velocities develop on one side of an ice sheet will the ratio ∆L/L have a large value.

Circular ice sheet

It is simple to show that Equation (6) determines the profile of a circular ice sheet if in that equation the radial distance r is substituted for the distance x _i , if the value of K is reduced by one half, and if the accumulation rate depends only on r and is independent of the azimuthal angle θ. Let L be the radius of such an ice sheet and let the value of L be fixed in value because of the presence of an ocean that surrounds the ice sheet.

Suppose that the accumulation rate is a function not only of r but also of θ. Where is the “center” (defined to be the position of the highest point of the ice sheet) of the ice sheet under these conditions? Limits on the position of the center can be made if the dependence of the accumulation rate is sufficiently weak so that the distance from the geometric center of the ice sheet to the highest point on the ice sheet is small compared with L.

Accumulation Rate Independent of Radial Distance r

Suppose the accumulation rate is independent of r but docs depend (weakly) upon θ. Let the bed of the ice sheet be flat either before or after the ice sheet is placed on it. Consider the cross-sectional profile of the ice sheet taken along the azimuthal angle θ. If the flow path of an ice particle in this cross-section lies entirety in the radial direction the cross-section can be calculated in a manner similar to that used for a two-dimensional ice sheet. The “ice divide” along this cross section has a position given by the equations

(19)

(20)

(21)

These equations are the analogues of Equations (9) and (11). In Equations (19), (20), and (21), a _θ is the accumulation rate along the azimuthal angle θ, L _θ the distance from the ice divide to the edge of the ice sheet, and ∆L _θ the distance from the geometric center of the ice sheet to the ice divide (see Fig. 4a). The quantities ∆a _θ and ∆L _θ can be positive or negative in value.

Fig. 4. (a) Circular ice sheet. (b) Position of “ice divide” and “center” (see text).

If the position of the ice divide is plotted for every angle θ, as is done schematically in Fig. 4b, a closed curve must result. It is reasonable to expect that the center of the ice sheet lies at about the center of the area enclosed by this curve. The closed curve of Figure 4b is found by assuming that the ice flow always is radial in direction. However if the accumulation rate has an azimuthal dependence the ice flow must have components in the azimuthal direction. It is this azimuthal flow that will cause shrinkage of the area enclosed by the curve of the ice divide of Figure 4b into an ice “center” point. The shift of the center of the ice sheet from its geometric center can be expected to be somewhat smaller than the maximum value of ∆L _θ calculated with Equations (19), (20), and (21).

Accumulation Rate that Varies Linearly with Radial Distancer

If the accumulation rate varies linearly with radial distance, a repetition of the calculation of the previous section leads to another closed curve for the position of the ice divide. The value of ∆L _θ is given by

(22)

Where

(23)

and c _θ is the rate of increase of the accumulation rate in the radial direction along the azimuthal angle θ. Equation (22) is valid when c _θ L/2b ⪢ 1, where b is the accumulation rate at the center of the ice sheet. If c _θ L/2b ⪡1 Equation (20) determines ∆L/L.

Conclusions

The model calculations that we have done show that rather gross changes must occur in the ratio of the average accumulation on different parts of an ice sheet whose edges are fixed in position before the center of the ice divide is shifted appreciably. The ratio must change by more than a factor of three before the shift in distance is greater than about 10% of the dimension of the ice sheet. The position of the edges of the lower three quarters of the Greenland ice sheet and almost all of the ice sheet of East Antarctica is fixed by the encircling seas. (There is a strip of exposed land along the south-east coast of Greenland.) We expect therefore that the positions of ice divides and ice domes on these portions of the Greenland and Antarctic ice sheets have not migrated appreciably in the past.