Multivariate parameter optimization for computational snow avalanche simulation

Abstract

Snow avalanche simulation software is a commonly used tool for hazard estimation and mitigation planning. In this study a depth-averaged flow model, combining a simple entrainment and friction relation, is implemented in the software SamosAT. Computational results strongly depend on the simulation input, in particular on the employed model parameters. A long-standing problem is to quantify the influence of these parameters on the simulation results. We present a new multivariate optimization approach for avalanche simulation in three-dimensional terrain. The method takes into account the entire physically relevant range of the two friction parameters (Coulomb friction, turbulent drag) and one entrainment parameter. These three flow model parameters are scrutinized with respect to six optimization variables (runout, matched and exceeded affected area, maximum velocity, average deposition depth and mass growth). The approach is applied to a documented extreme avalanche event, recorded in St Anton, Austria. The final results provide adjusted parameter distributions optimizing the simulation–observation correspondence. At the same time, the degree of parameter–variable correspondence is determined. We show that the specification of optimal values for certain model parameters is near-impossible, if corresponding optimization variables are neglected or unavailable.

Introduction

Snow avalanche simulation tools are used for hazard estimations and protection planning (Sampl and Zwinger, 2004; Christen and others, 2010a). Initial conditions and flow model parameters have to be defined carefully to obtain meaningful simulation results. The challenges arising in this process are manifold. Existing avalanche dynamics models contain parameters some of which are more conceptual than physical. A direct calibration, i.e. measuring the specific material parameters in the field directly, is hardly possible. Existing guidelines provide model parameter suggestions or estimates for release conditions for extreme avalanches (Salm and others, 1990; Maggioni and Gruber, 2003; Gruber and Bartelt, 2007). They are used to quantify avalanche danger for hazard scenarios with different return periods. Back calculation of real avalanche events requires modification of these parameter suggestions to include physical processes such as flow regime transitions (Issler and Gauer, 2008; Bartelt and others, 2012) as well as the effects of snow temperature and entrainment (Naaim and others, 2013; Vera Valero and others, 2015). Only then is it possible to reproduce observed runout, flow velocities, impact pressures and deposition depths. However, at present it is still not clear whether process-oriented models can be used in engineering practice since they demand the specification of detailed snow-cover and release information. Therefore there is still an urgent need to find an optimization method to establish model parameters for hazard scenarios solved with existing simulation software in avalanche practice.

Early optimization approaches date back to Dent and Lang (1980, 1983), who utilized velocity and deposition data from single snow-flow test experiments to fit model parameters. This work was followed by, for example, Ancey and others (2003), who introduced a deterministic inversion method, finding a parameter distribution for a simplified flow model, reproducing avalanche runouts. Besides deterministic approaches, there has been a strong development of probabilistic (especially Bayesian) frameworks originating from the hydrological community. These developments were accompanied by debates concerning different (formal and informal) optimization strategies (Beven and Binley, 1992; Vrugt and others, 2008). The main issues concern the arising quantification of uncertainty (Montanari and others, 2009).

In the field of snow and avalanches, several authors (Ancey, 2005; Eckert and others, 2007, 2008; Gauer and others, 2009) have employed Bayesian techniques to solve the inverse problem for lumped mass propagation models and avalanche runout, by, for example, analyzing occurrence frequencies for multiple avalanche paths. Naaim and others (2013) employed this method to link model parameters to physical properties of snow. However, challenges in the model validation arise, because formal Bayesian approaches explicitly consider model input and parameter uncertainty (Vrugt and others, 2008). Therefore the individual error sources have to be identified and quantified in order to assign the resulting probability to one of them (Beven and others, 2008; Vrugt and others, 2008). This problem is especially severe with regard to avalanches because of the interaction of input and parameter uncertainty (Eckert and others, 2010). For example, Ancey (2005) showed the dependence between a frictional parameter and input parameters such as avalanche volume and snow properties for a sliding-block model.

Informal statistical approaches, to which the proposed method is similar, do not explicitly consider model uncertainties (McMillan and Clark, 2009). They are based on a more arbitrary function to quantify the correspondence between simulation results and observation. With this objective measure, adjusted parameter distributions can be computed. At the same time, these resulting distributions represent an estimate of total uncertainty. Despite the differences between informal and formal Bayesian approaches it has been found that they can yield very similar estimates of the total result uncertainty (Vrugt and others, 2008).

The application of optimization methods with simulation tools operating in three-dimensional (3-D) terrain is limited. Most studies of avalanche simulation tools are based on multi-parameter models, but they have mostly been optimized for single optimization variables, namely the avalanche runout (Ancey, 2005; Gruber and Bartelt, 2007; Bozhinskiy, 2008). Providing single constraints is insufficient to obtain a unique multivariate parameter set. Information on flow variables (e.g. velocity) is rarely accessible and is therefore used in few case studies (Sailer and others, 2002; Ancey and Meunier, 2004; Issler and others, 2005; Gauer and others, 2009; Fischer and others, 2014). In cases where no information is available, empirical analysis can provide rough estimates for missing measurements. For example, the analyses of McClung and Schaerer (2006) allow us to estimate the maximum avalanche velocity by scaling it with the total fall height along the avalanche path. The estimate is based on basic energy relations, recently confirmed for a variety of extreme avalanches (Gauer, 2014).

The main focus of the presented optimization concept is to provide adjusted parameter distributions employing a systematic, multivariate comparison of simulation results with field observations and their related uncertainties. The proposed framework is sketched in Figure 1. It is tested for a catastrophic avalanche. A simple, three-parameter flow model including entrainment is employed and implemented in the operational snow avalanche simulation software, SamosAT (Snow Avalanche MOdelling and Simulation – Advanced Technology) (Zwinger and others, 2003; Sampl and Zwinger, 2004). A large number of simulation runs is performed following an input parameter distribution. The results are analyzed in an avalanche path dependent coordinate system (Fischer, 2013). The multivariate parameter optimization is carried out with respect to three varying model parameters and six different optimization variables, enabling the quantification of simulated and observed avalanche characteristics. By introducing a selection rule, parameter combinations with optimal simulation–observation correspondence are identified. The main results are problem-suited parameter distributions. These adjusted distributions provide peak values for the flow model parameters leading to an optimized simulation result and provide a base for future guidelines.

Fig. 1. The proposed framework consists of three parts: observation, simulation and optimization. Monte Carlo simulation runs are performed for a large number of parameter combinations Θ = μ, ξ, e_b following the input parameter distributions . The simulation software, SamosAT, is utilized, taking into account boundary and initial conditions, which are obtained from the observations. The set of optimization variables X = {…} (with variables runout r, matched affected area (true) T, exceeded affected area (false) F, maximum velocity u _max, average deposition depth d and mass growth G) is defined in terms of the simulation results (flow depths h, velocities u and mass m of the avalanche) as well as observations and their related uncertainty . The simulation–observation correspondence α(Θ) is quantified for each simulation run. Based on a consistently defined correspondence limit α _lim, parameter combinations are withdrawn or accepted, yielding the final results: adjusted parameter distributions Ω_Θ.

Simulation Concept

The simulation concept comprises the choice of

1. 1. the simulation software including the physical flow model and its numerical implementation (simulation

2. approach)

3. 2. the initial and boundary conditions, including the digital elevation model (DEM), initial distribution of snow and the model parameter settings (simulation input)

4. 3. the survey and interpretation of simulation results in view of the model evaluation, and the comparison to the field observations (simulation output).

Simulation approach

Simulation software for the dense, most destructive part of snow avalanches is based on two-dimensional depth-averaged, deterministic flow models (Savage and Hutter, 1989; Naaim and others, 2002; Pitman and others, 2003; Sampl and Zwinger, 2004; Christen and others, 2010b; Mergili and others, 2012; Pudasaini, 2012). An adequate mathematical description requires switching between different coordinate systems. The following model equations will be written in a Lagrangian framework using the notation for flow variables depth and velocity and the mountain surface in a natural coordinate system moving with the avalanche. In the Eulerian framework, variables and surface are denoted h, u, z with respect to the coordinate system aligned with the avalanche path. The mountain surface is represented by a DEM with a spatial resolution of 5 m × 5 m, which is assumed to represent the winter, snow-covered surface sufficiently. Sampl and Zwinger (2004) presented a Lagrangian formulation of the mass and momentum balance, describing the spatio-temporal evolution of the primary variables: depth-averaged flow depth and velocity (Iverson, 2012). Here the equations are formulated for an incompressible, isotropic material, with a general basal shear stress τ_b and an entrainment rate , integrated over an infinitesimal control volume , that moves with the avalanche (Zwinger and others, 2003). This yields a locally orthogonal coordinate system. i = 1 is in the direction of the surface-parallel velocity vector, i = 2 is surface-parallel and orthogonal to the velocity vector and i = 3 appears naturally normal to the surface :

(1)

(2)

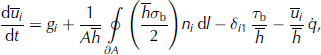
with the components of the gravitational acceleration g_i , the surface-parallel velocity components u ₁, ū ₂, the surface-normal flow depth and the resulting normal stress . The term accounts for the change in the normal acceleration due to surface curvature in the flow direction (Gray and others, 1999; Pudasaini and Hutter, 2003; Fischer and others, 2012). The first term on the right-hand side of Eqn (2) accounts for the acceleration due to gravity. The second term arises due to the pressure gradients on the control volume V, with boundary line ∂A with elements dl and the normal vector n_i (Zwinger and others, 2003). The third term describes the frictional decelerations opposing the direction of movement i = 1, with the Kronecker delta δ_ij . The last term arises due to the modified mass balance (right-hand side of Eqn (1)) and causes a momentum loss if additional mass has to be accelerated by the avalanche.

Equations (1) and (2) are solved with a smoothed particle hydrodynamics (SPH) scheme (Monaghan, 1992) for the three variables ū = (ū ₁, ū ₂) and depth , by discretization of the released avalanche volume in a large number of mass elements. The number of mass elements is calculated in accordance with the claim that the mass per numerical particle is ∼2000 kg (cf. Sampl and Zwinger, 2004). The simulation end time t _end was chosen carefully according to the criterion that the pressure isoline of p = p _lim showed no significant changes over time, which was sufficiently reached with t _end = 350 s for the specific avalanche simulations (Fischer, 2013; Teich and others, 2014). The total duration of a computation is in the order of several minutes with a standard computer.

Basal shear stress τ _b and entrainment rate

Over the years many different (mostly phenomenological) friction and entrainment relations have been implemented in different flow models (Harbitz, 1998). The goal of this work is not to discuss or compare different approaches but to show that a systematic, multivariate parameter optimization is possible. Therefore the well-known Voellmy friction relation for the basal shear stress and a simple assumption for the entrainment rate are employed. The basal shear stress τ _b combines a Coulomb bottom friction with a velocity-dependent drag term:

(3)

with dimensionless friction parameter μ and turbulent friction coefficient ξ(m s⁻²) (Voellmy, 1955).

The entrainment rate,

(4)

is proportional to the bottom shear stress τ _b, which is similar to other definitions found in the literature (Christen and others, 2010b), and includes the phenomenological parameter e_b (m² s⁻²), which allows for interpretation as specific erosion energy. For small parameter values e_b → 0 the entrainment rate is very large, ; however, independently of the entrainment rate, the amount of entrained snow is limited by the available snow reservoir q < h _snow (cf. Eqn (5) below). Entraining the entire snow reservoir h _snow at the flow front corresponds to the process of frontal plowing. Larger e_b values allow for a gradual erosion, from the front to the tail of the avalanche (Gauer and Issler, 2004). For large parameter values e_b → ∞ the entrainment rate diminishes , i.e. no snow is entrained.

Simulation input

To perform snow avalanche simulations, parameter set-up for the employed flow model and initial conditions have to be defined.

Initial conditions

For the presented analysis, initial conditions are assumed to be constant and are estimated through direct measurement or empirical methods. Release areas are either delineated by direct event observation or a set of empirical rules, which are mainly based on slope and planar curvature (Maggioni and Gruber, 2003; Bühler and others, 2013). Typically the initial distribution of released snow is either directly measured or estimated by means of an extreme snowfall. The estimated snow depth h ₀ is often linked to the sum of new snow over 3 days for a certain return period (Burkard and Salm, 1992) measured on flat ground at a reference altitude z ₀.

Here we estimate a smooth initial snow-cover distribution h _snow, assuming equal precipitation at each location. This approach allows us to determine the initially released snow mass and the potentially erodible snow mass in a consistent manner. Precipitation varies with altitude through the snow depth–altitude gradient Δh. The influence of wind transport is neglected:

(5)

θ is the local slope angle. The snow depth gradient Δh is a regional coefficient and varies for different precipitation characteristics (Burkard and Salm, 1992). The smooth snow distribution leads to lower (higher) snow depth on steep (flat) slopes. Once the avalanche is released, the snow reservoir h _snow is depleted inside the release area and evolves over time. for the rest of the mountain surface.

Reference event

Documentation of extreme events characterizing processes in terms of release conditions, flow path and runout zone provides important information for performing hazard assessment and model optimization. The Wolfsgruben avalanche path starts in a release area of ∼20 ha, with mean slope angle 36.5° at ∼2244 m a.s.l. It follows a gully, with a width of ∼100 m, and finally reaches the community of St Anton a.A., Austria (at ∼1260 m a.s.l.; Fig. 2). On 13 March 1988 a catastrophic avalanche struck the village, affecting an area of ∼6.5 ha with mean slope angle of 14.5°. The avalanche led to severe loss of life and property. Three houses and nine cars were destroyed, and several other buildings, about 20 cars and existing infrastructure were damaged (back-calculated pressures range between about 7.5 and 17.5 kPa). Several people were killed or injured. The event return period has been estimated to be sufficiently large to serve as a design event (>150 years in Austria; cf. johannesson and others, 2009).

Fig. 2. Wolfsgruben avalanche (images WLV). (a) Wolfsgruben avalanche path (vertical drop Δz = 984 m): central flowline in black, release area (196 225 m², with mean slope angle 36.5°) in blue, affected area (64 153 m², at 14.5°) in orange. (b) Destroyed house in the runout area. Back-calculated pressures of damages on infrastructure range from about 7.5 to 17.5 kPa.

The observations allow us to reconstruct the initial snowcover distribution h _snow of the event, with reference snow height of h ₀ = 1.61 m at z ₀ = 1289 m a.s.l. and a snow-depth–altitude gradient of Δh = 8cm (100 m)⁻¹ for the Arlberg region. Considering Eqn (9) and the given topography this information leads to a total release volume of V _release ≈ 354 600 m³. The snow reservoir depth for entrainment ranges between about 0.6 and 1.8 m. Besides basic observations of snow avalanches (e.g. the delineation of release areas, affected path and runout zone), information on physical properties like deposition depth (∼4 m) and density (∼400 kg m⁻³), as well as flow velocity, is essential for the parameter optimization. This information allows us to define optimization variables (e.g. runout, maximum velocity or mass growth), which are related to the avalanche (Table 1; next section).

Table 1. Observational variables for the Wolfsgruben avalanche

Flow model parameters Θ = {μ, ξ, e_b }

For the presented optimization the input parameter distributions, given by , yield simulation samples of size N. For each simulation run, a set of flow model parameter combinations Θ _n = {μ_n , ξ_n , e_{b , n} } with n = 1, … , N is assigned. The number of simulation runs N in a sample has to be sufficiently large that the obtained results are statistically significant and stable (N ≳ 8000; cf. Analysis subsection below, ‘investigating the statistical significance’). Plausible combinations of input parameters for the deterministic flow model are obtained through a Latin hypercube sampling (Stein, 1987). This sampling method provides a probabilistic representation of the input distributions dividing the range of each variable into equally probable intervals. The flow model parameters Θ = {μ, ξ, e_b } are assumed independent. Naturally the random samples include a certain degree of correlation. Since independence in the input samples is desirable, a correlation control is applied on the initial parameter sample (Oberguggenberger and others, 2009; Fischer and others, 2014). With this empirical method the parameter samples are rearranged in order to get closer to parameter independence (i.e. close to a diagonal rank correlation matrix; Iman and Conover, 1982).

The input parameter distributions are specified by their distribution function and the related parameter range. Since the estimation of the adjusted distribution for a specific event is a goal of the analysis, we assume an equal distribution function for the input samples, which leaves the parameter ranges to be specified. Assigning the parameter ranges too small may exclude possible solutions; defining the ranges too large multiplies the computational efforts. The interval bounds may be constrained by the physically relevant parameter space, values found in the literature or results of experimental work.

For example, considering the limits μ → 0, ξ → ∞ or e_b → ∞, the effect of Coulomb friction, turbulent friction or entrainment is negligible. In contrast, the limits μ → ∞, ξ → 0 lead to infinite friction, i.e. the avalanche cannot move; e_b → 0 corresponds to entrainment by frontal plowing, which may initiate uncontrolled mass gain, often accompanied and identifiable by unrealistic lateral spreading of the avalanche. In practice, the limits do not coincide with 0 or ∞ but may be determined by scaling analysis of the respective terms in the model equations. Taking into account values of back calculations for similar flow models allows us to further specify the parameter ranges. Voellmy (1955) estimated values in the range μ = 0.08–0.15 and ξ = 400–600 m s⁻². Gubler (1987) used velocity data, finding different values for the Coulomb friction in the path and the runout zone, in the range μ = 0.15–0.5. For practical purposes different authors have recommended different values. For example, Buser and Frutiger (1980), Salm and others (1990) and Gruber and Bartelt (2007) (often referred to as Swiss Guidelines) proposed Coulomb friction values μ = 0.155–0.3 and turbulent friction coefficients ξ = 400–1000 m s⁻² depending on different variables such as return period, avalanche size or terrain features. Barbolini and others (2000) found Coulomb friction values between 0.13 and 0.4 and turbulent friction coefficients between 1000 and 4500 m s⁻² for different models and sites. Naaim and others (2010) fixed ξ to 1500 m s⁻², obtaining μ values between 0.15 and 0.35 based on historical data from the avalanche path Taconnaz. In a similar framework, Naaim and others (2013) scanned values for the static Coulomb friction from 0.1 to 0.7 and turbulent friction from 500 to 1500 m s⁻². However, with some exceptions (Sovilla and others, 2007; Bozhinskiy, 2008; Naaim and others, 2013), snow entrainment is disregarded or not explicitly treated. Parameter specifications derived by experiments fit in similar ranges; for example, experiments performed on snow chutes by Tiefenbacher and Kern (2004) and Platzer and others (2007) allowed estimation of an effective Coulomb friction of μ = 0.22–0.72. However, in the present context, friction coefficients appear more conceptual than physical.

Based on this, we specify the following parameter range specifications for the equally distributed input parameters , ξ =[400, 15 000 m s⁻² and e_b = [0, 75 000] m² s⁻², with minimal spacing Δμ = 0.01, Δξ = 50 m s⁻², Δe_b = 250 m² s⁻².

Simulation results

Primary simulation results are the time evolution of flow depth and velocities. However, the most important simulation results for the evaluation are the peak values, i.e. maximum values over time, of flow depth h, velocity |u| and impact pressure p = ρ |u| ², with ρ = 200 kg m⁻³, the density of flowing snow. The formulation of impact pressure is chosen according to guidelines used for avalanche simulations but may differ significantly from this general form (Sovilla and others, 2008). Defining runout or impacted area in terms of impact pressures is in accordance with avalanche hazard mitigation guidelines (Johannesson and others, 2009; Fischer, 2013; Teich and others, 2014). However, they could equivalently be defined in terms of velocities. The simulation results are evaluated in an avalanche path dependent coordinate system, with flow-path coordinate s and lateral coordinate l, according to the main flow path shown in Figure 2a with a domain width of 500 m (Fischer, 2013).

Optimization Variables

The optimization variables represent the different categories that are accessed through the observational data and simulation results. To perform an objective analysis, a set of six optimization variables X = {r, T, F, u _max, d, G},

1. 1. runout r

2. 2. matched affected area (true) T

3. 3. exceeded affected area (false) F

4. 4. maximum velocity u _max

5. 5. average deposition depth d

6. 6. mass growth G,

is defined in terms of both observation and simulation. Observational variables and their associated uncertainty are denoted by (Table 1), simulation variables by plain X. In this work we do not explicitly account for simulation uncertainties introduced by the deterministic flow model. The information about the source of uncertainty is dispensable for the employed optimization concept. Thus simulation uncertainties can implicitly be associated with the uncertainty of the corresponding observational variable .

Runout r

The definition of avalanche runout in the sense of a simulation and observation is not straightforward, especially in 3-D terrain. Here we define a peak impact pressure related runout in an avalanche-dependent coordinate system. Utilizing a pressure-related measure as runout has several advantages for operational simulation tools (Fischer, 2013; Teich and others, 2014). For each simulation run, runout r refers to the farthest coordinate s, measured as projected distance in the avalanche-path flow direction, where the maximum value of the peak impact pressure in the cross section still exceeds the predefined pressure limit p _lim, i.e. max _l p(s, l) > p _lim. Here we set p _lim =1 kPa, which may be adapted for different hazard-mapping guidelines.

To determine the observational runout the affected area is dealt with in exactly the same manner as the simulation pressure results, assuming peak impact pressures larger than the pressure limit, , inside the observed affected area (Fig. 3). The uncertainty associated with the delineation of the affected area is the range of .

Fig. 3. Sketched simulation results (e.g. simulation outline p _lim; blue) and affected area (orange), superimposed with avalanche path domain and coordinate system along the central flowline (black). Runout r, , matched area A _matched (green) and exceeded area A _exceeded (red) and their complements (blue and gray area), which lead to the optimization variables for true and false prediction T, F, maximum velocity u _max, average deposition depth d and mass growth G.

Relative matched and exceeded affected area, T, F

Peak impact pressures serve as a basis to define observed and simulated affected areas, assuming that peak pressures observed in the avalanche exceed the pressure limit p _lim, i.e. inside the observed affected area. Comparing the simulated and observed affected areas, four different classifications arise. The four cases include all combinations of matching/non-matching or exceeding/non-exceeding observed area with simulated affected area (cf. the four differently colored areas in Fig. 3; Mergili and others, 2013). Considering the given affected and total area, two of them are independent. The optimization variables T and F for matching and exceeded areas are defined relative to the affected area and are specified as:

true prediction T = A _matching/A _affected – simulated area with p > p _lim matching observed affected area ,

false prediction F = A _exceeded /A _affected – simulation area with p > p _lim exceeding observed affected area .

It is crucial to consider the main flow direction, represented by the path coordinate s (Fischer, 2013), since information on affected areas is mainly available in the runout. To properly account for the false prediction, only areas beyond (in flow direction) the path coordinate s, where , are considered, due to lack of observations in the upstream direction.

The observational value for the optimization variable true prediction T = A _matching/A _affected is given by , and consequently for the false prediction F = A _exceeded/A _affected by . For the situation sketched in Figure 3 the respective simulation variable values could be approximated to T ≈ 0.7 and F ≈ 0.05. The associated uncertainty is estimated and expressed relative to the affected area .

Maximum velocity, u _max

The maximum velocity u _max is defined for each simulation run by taking the maximum of the peak velocities over the entire simulation domain:

(6)

The observational value for the optimization variable along an avalanche path with fall height Δz is empirically estimated bt (McClung and Schaerer, 2006). For the investigated Wolfsgruben avalanche path the maximum velocity is , which is a reasonable value for avalanches of that size (Gauer and others, 2007; Fischer and others, 2014). The associated uncertainty may be determined by regression (Gauer, 2014) and is estimated at .

Average deposition depth d

The average deposition depth is defined as observed depth, averaged in the affected area. It can be directly measured in the field. The documentation by avalanche experts for the Wolfsgruben avalanche includes deposition depths between 3 and 5 m with a density of . This allows the estimate .

Densification in snow avalanches, comparing released, flowing and deposited snow, can reach a factor of three (Ancey, 2005). Thus, the average deposition depth needs to be defined in terms of the simulation results. We take the peak flow depth h and define averaged in the affected area.

Mass growth G

The mass growth index G is a dimensionless number, describing the increase of flowing avalanche mass due to entrainment. It is defined as the ratio of deposited to released mass

(7)

and has been measured for a variety of avalanche events. However, measurements of the growth index are associated with large variations and uncertainties (Sovilla and others, 2006, 2007), for example due to the densification (Ancey, 2005).

Considering densification, released snow mass, affected area and documented deposition depths leads to an estimate of for the Wolfsgruben avalanche.

In terms of the avalanche simulations (cf. Eqns (1) and (4)) the growth index may be written as

(8)

Optimization Concept

The goal of the optimization concept is to provide an objective function as an intuitive, scalar metric, describing the correspondence between simulation and documentation in different categories. The metric allows us to perform a ranking, determining simulation runs and according parameter sets with the highest correspondence to the observation. This matches a selection rule allowing us to accept or withdraw certain parameter combinations, providing input distributions and yielding problem-suited, adjusted output parameter distributions Ω_Θ, representing optimal parameter combinations. A flow chart of the optimization concept is depicted in Figure 1. The resulting parameter distributions include model and parameter uncertainties and are of fundamental interest for engineers and scientists.

Using the target function presented here, the optimization of the model parameters could be performed straightforwardly with a Gauss–Newton algorithm, or – more appropriately for the usually coarse DEM grid – a simplified gradient method (Sailer and others, 2008). The numerical gradients (Jacobian) obtained in such methods for the optimal parameter set could be used for first-order sensitivity studies (Fellin and Ostermann, 2006). However, such inverse calculations are not unique and several local minima could exist. Depending on the initial guess of the model parameters, one of these local minima is found and could be falsely seen as the global minimum, so that a wrong optimal parameter set is chosen (cf., e.g., Ancey, 2005). Investigating the whole physically relevant parameter space and performing statistics on the best simulation runs as proposed here is computationally more expensive, but much more information is produced: local minima can easily be detected and excluded, a complete sensitivity analysis can be performed (Fischer, 2013) and reasonable ranges of the model parameters can be determined.

As a measure of the correspondence between observational and simulation optimization variables, we determine α_{X (Θ)} for each optimization variable X = {r, T, F, u _max, d, G}, conditional upon the choice of the parameter set Θ = {μ, ξ, e_b } summarized in a target function α(Θ). The function describing the correspondence is chosen to be a normalized, Gaussian function with mean and variance :

(9)

A metric is then defined in the interval [0, 1], where α_{X (Θ)} → 0 indicates negligible correspondence and α_{X (Θ)} → 1 optimal correspondence between observation and simulation with respect to the investigated optimization variable. However, the choice of the Gaussian function is arbitrary and it could be replaced by another function (e.g. Heaviside, triangle).

The final correspondence target function α(Θ) is defined as

(10)

With , such that α(Θ) is also bounded by the interval [0, 1]. A ranking of α allows for determining the parameter set Θ with optimal agreement between observation and simulation. The results of the optimization clearly depend on the non-unique definition of the target function, which is a heuristic construction (e.g. not accounting for dependencies between the different optimization variables). The weighting factors w_X allow us to emphasize or reduce the impact of certain optimization variables X. For the presented investigation the weighting factors are kept equal, with the exception of excluding single optimization variables. For example, if no information on the variable is available it may not be included in the optimization process, corresponding to a zero weighting factor w_X = 0 and a reduced set of optimization variables. The optimization procedure can then be adapted to cases with more or fewer observational data.

Defining a limit α _lim matches a selection rule, where simulation runs with a simulation–observation correspondence larger than the limit α(Θ) ≥ α _lim are accepted and the other parameter combinations with α(Θ) < α _lim are withdrawn. The correspondence limit α _lim may be a user-defined value or, in accordance with other engineering applications, be defined in terms of a design event α _design (e.g. assuming an acceptable deviation of 5% for each observational variable ). The resulting parameter distributions (including parameter and model uncertainties) then allow us to determine characteristic values for actions, which are based on certain quantiles in engineering concepts like the Eurocodes. Thus, in terms of design events, the limit α _lim = α _design is calculated following Eqn (10):

(11)

For the simulation runs with α(Θ) ≥ α _lim, a frequency analysis of the model parameters Θ is performed. The frequency distribution yielding the adjusted distribution Ω_Θ is analyzed for each parameter of the model parameters Θ = {μ, ξ, e_b }. The adjusted distribution Ω_Θ allows us to further investigate the model behavior. Of particular interest are statistical features, such as the 25%, 50% (median) and 75% quantiles for each parameter Θ_25%, Θ_50%, Θ75%, minimum and maximum values Θ_min, Θ_max and the parameter value that correspond to the highest simulation–observation correspondence, i.e. maxα (Θ). Additionally, violine plots (Kampstra, 2008) are a helpful tool for visual interpretation of the adjusted distributions, showing an approximate form of the frequency distribution (Fig. 4).

Fig. 4. Adjusted parameter frequency Ω_Θ for the simulation runs with α ≥ α _lim. The violine plot above summarizes statistical features of the adjusted distributions Ω_Θ such as the minimum value Θ_min the 25%, 50% and 75% quantiles Θ_25%, Θ_50% and Θ_75% and the maximum value Θ_max. To provide a reference to the input distribution the minimum and maximum values are shown.

Analysis of Adjusted Output Parameter Distributions Ω_Θ for Θ = {μ, ξ, e_b }

The analysis of the output parameter distributions Ω_Θ is carried out, varying the set-up with respect to:

optimization variable weighting factors w_X , i.e. changing the size of the optimization variable set X = {r, T, F, u _max, d, G},

the simulation–observation correspondence limit α _lim, the sample size N.

Full set of optimization variables X = {r, T, F, u _max, d, G}, N = 10⁴, α_lim = α_design

Here we consider the full set of optimization variables X = {r, T, F, u _max, d, G}, with N = 10⁴ sample size of the input parameter distribution at a correspondence limit α _lim = α _design. Figure 4 shows the adjusted output parameter distributions Ω_Θ with . For Ω _μ and a clear peak is found, i.e. Θ_25%, Θ_50%, Θ_75% and are relatively close (Table 2). The distribution Ω _ξ indicates the tendency of ξ to only provide the desired simulation–observation correspondence lim above a certain boundary value around 7500 < ξ (m s⁻²). However, no clear peak tendency for ξ is found, which is underlined by the fact that is outside the 75% quantile.

Table 2. Information on the adjusted output parameter distributions Ω_Θ, for different sets of optimization variables X. Listed are minimum and maximum values Θ_min, Θ_max, 25%, 50% and 75% quantiles for each parameter Θ_25%, Θ_50%, Θ_75% and . The same data are visualized in Figure 6

Range and sensitivity of simulated optimization variables X with respect to the adjusted output parameter distributions Ω_Θ

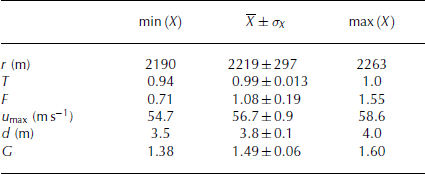
The range of simulated optimization variables (X; Table 3) allows us to estimate the quality of the performed back calculation. Simulated runouts are in the range 2190–2263 m with an average value of , which corresponds to the observed range (Table 1). Similar correspondences are obtained for all optimization variables.

Table 3. Distribution of simulated optimization variables X = {r, T, F, u _max, d, G} with adjusted output parameter distributions Ω_Θ and α _lim = α _design. denotes the average, and σ_X the variance

Helpful information to interpret the resulting parameter distributions Ω_Θ is the quantification of the flow model parameter Θ sensitivity with respect to the optimization variables X. A Spearman rank correlation analysis is performed (Fischer, 2013). The correlation coefficients range from −1 to +1, −1 indicating negative monotonic correlation (increasing parameter leads to decreasing variable), +1 indicating positive monotonic correlation (increasing parameter leads to increasing variable) and 0 indicating no correlation. Table 4 summarizes the parameter-optimization variable correlation coefficients. Besides the obvious relations, which reflect the meaning of the parameters in the employed flow model (e.g. increasing friction leads to decreasing runout or velocities; entrainment rate determines growth index), the quantification allows for a relative evaluation. The information that turbulent and Coulomb friction equally influence the maximum velocity or that no parameter but e_b significantly influences the deposition depth is important for model tweaking and the interpretation of the adjusted parameter distributions, especially with respect to a reduced set of optimization variables.

Table 4. Information on the correlation of the adjusted parameter distributions Ω_Θ and the optimization variables X. Shown is the Spearman (rank) correlation coefficient r _s of optimization variables X and parameters Θ. Only highly significant (p < 0.01) correlations with ∥r _s∥ > 0.25 are shown

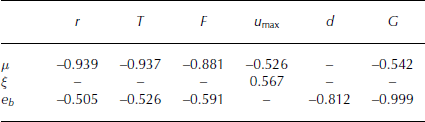
Reduced set of optimization variables X, N = 10⁴, α _lim = α _design

With two examples we highlight the benefits of a multivariate parameter optimization. The multivariate parameter optimization is based on a set of different optimization variables X = {r, T, F, u _max, d, G}; reducing this set has a significant effect on the adjusted output parameter distributions Ω_Θ and thus the ability to quantify optimal parameter set-ups. To investigate the effect, we manipulate the correspondence target function (Eqn (10)), excluding certain optimization variables X by changing the related weighting factors w_X = 0.

Reduced set of optimization variables X = {r, T, F, d, G}, i.e.

Excluding the optimization variable u _max by setting has a considerable effect on the adjusted output parameter distributions, in particular on the ξ distribution Ω _ξ . Figure 5 shows the adjusted parameter distributions Ω_Θ with . For μ and e_b clear peaks are observed, i.e. the values of μ _25%, μ _50%, , μ _75% and e _b,25%, e _b,50%, , e _b,75% are very close (Table 2). For μ few additional outliers with small values are observed. Investigating the adjusted distribution Ω _ξ , only very small constraints for optimal ξ values can be drawn. Besides the effect that no high simulation–observation correspondence solutions are found for small ξ < 1300 m s⁻², ξ values are found in the entire investigated range evenly distributed.

Fig. 5. Adjusted parameter frequency Ω_Θ for the simulation runs with α ≥ α _lim: (left) ; (right) W_G = W_d = 0. The violine plot above summarizes statistical features of the adjusted distributions Ω_Θ such as the minimum value Θ_min the 25%, 50% and 75% quantiles Θ_25%, Θ_50% and Θ_75% and the maximum value Θ_max. To provide a reference to the input distribution the minimum and maximum values , are shown.

Reduced set of optimization variables X = {r, T, F, u_max}, i.e. w_G = w_d = 0

Excluding the optimization variable average deposition depth d and growth index G has little effect on the adjusted output distribution Ω _μ but significantly influences the output ξ and e_b distributions (Fig. 5). The number of simulation runs above the correspondence limit α _lim is . While clear constraints are found for μ, the distributions Ω _ξ and are spread out in almost the entire investigated range (Table 2). Interestingly, ξ values are spread evenly in the investigated interval with a lower bound at ξ _min = 5300 m s⁻². This means for ξ > ξ _min the chances are equal of finding ξ values that lead to simulation runs with simulation–observation correspondence α ≥ α _lim, which is also reflected by the fact that the parameter value leading to highest correspondence is found at the upper bound of the investigated range . For only a lower bound is found, e_b > e_{b , min = 6250} m² s⁻², corresponding to an exclusion of simulation runs with frontal plowing as entrainment mechanism.

Comparison of different sets of optimization variables X

Excluding single or multiple optimization variables has a significant effect on the information value of adjusted output parameter distributions Ω_Θ. The different examples show that form and range of the adjusted parameter distributions significantly varies. Results are summarized in Table 2 and Figure 6 for a visual interpretation of the violine plots. For the presented cases the distribution Ω _μ is hardly influenced by the reduced set of optimization variables. The adjusted distribution is unaffected by missing knowledge about the maximum velocity u _max but heavily influenced by the optimization variable G. This observation is not surprising, taking into account the correlation of optimization variables and model parameters. Excluding information on maximum velocity u _max significantly decreases the information value of the adjusted distribution Ω _ξ . A similar effect, but much less pronounced, is observed for leaving out average deposition depth d and growth index G. However, all adjusted output distributions Ω _ξ have one thing in common, a lower ξ value bound for high simulation–observation correspondence.

Fig. 6. Comparison of violine plots for the adjusted output parameter frequency Ω_Θ for the three cases: (1) all optimization variables (Fig. 6); (2) ; and (3) w_G = w_d = 0 (Fig. 5). The violine plots summarize statistical features of the adjusted distributions Ω_Θ such as the minimum value Θ_min the 25%, 50% and 75% quantiles Θ_25%, Θ_50% and Θ_75% and the maximum value Θ_max. To provide a reference to the input distribution , the minimum and maximum values are shown. The same data are summarized in Table 2.

Full set of optimization variables X, N = 10⁴, varying α_lim

The choice of the correspondence limit α _lim determines the number of simulation runs with α ≥ α _lim. Figure 7 shows the nonlinear decrease of with increasing α _lim. Above a certain limit α _lim > 0.75, no simulation runs are found, i.e. . For α _lim < 0.2, increases dramatically. This can be interpreted as residual correspondence and is due to the fact that some optimization variables are complementary (e.g. an avalanche reaching the affected area implies α_{T ,d} = 0 but α_F = 1). For α _lim = 0 it naturally is . Figure 8 shows the evolution of the adjusted output distributions Ω _μ in dependence on the α _lim. Lower α _lim lead to larger bounds of Ω_Θ, depending on the parameter Θ, i.e. for Ω _ξ . In the presented example Ω_Θ converges to for large correspondence limits α _lim. This is an important observation since multiple distribution maxima may also exist (cf., e.g., Ω _μ for α _lim = 0.15).

Fig. 7. Number of simulation runs , that are assigned to the adjusted parameter distributions Ω_Θ, i.e. with sufficiently large simulation–observation correspondence α ≥ α _lim.

Fig. 8. Comparison of violine plots for the adjusted output parameter frequency Ω_Θ for varying α _lim. The violine plots summarize statistical features of the adjusted distributions Ω_Θ such as the minimum value Θ_min, the 25%, 50% and 75% quantilesΘ_25%, Θ_50% and Θ_75% and the maximum value Θ_max. To provide a reference to the input distribution the minimum and maximum values are shown.

Full set of optimization variables X, α_lim=α_design, variable sample size N, investigating the statistical significance

To determine the statistical stability and draw conclusions on the significance of our results we investigate the dependence of Ω_Θ on N. To do so we employ a bootstrapping technique drawing random samples of size N from the sample with 10⁴ simulation runs, increasing the sample size N = 250, … , 10⁴. A first observation is that is directly proportional to sample size N indicating the equal random distribution of the full sample. The minimum sample size for statistically stable results is reached when the parameter distributions stay constant for increasing sample size N (e.g. when Θ₅₀ converges for increasing sample size N).

In the presented case the changes on Ω_Θ appear negligible when the sufficient sample size N ≳ 8000 is reached (Fig. 9). Between 3000 < N < 8000 the results are intermediately stable. However, if N is chosen too low, in the presented case N ≳ 2000 the adjusted output distributions are not stable and one may identify statistically non-significant parameter choices, i.e. is too low.

Fig. 9. Comparison of violine plots for the adjusted output parameter frequency Ω_Θ for varying sample size N. The violine plots summarize statistical features of the adjusted distributions Ω_Θ such as the minimum value Θ_min the 25%, 50% and 75% quantiles Θ_25%, Θ_50% and Θ_75% and the maximum value Θ_max. Note the scale of the parameter ranges.

One should note that the minimum sample size is dependent on , which is a function of α _lim and directly proportional to the sample size N itself. For example, with α _lim ≈ 0.4, N ≈ 4000–5000 appears to be sufficient. For smaller N, which corresponds to the situation where the input parameter distribution is not well chosen, the optimal parameter distribution Ω_Θ may vary significantly. However, it is beyond the scope of this work to derive a general rule determining the sufficient sample size.

Conclusions

A new optimization concept for snow avalanche simulation has been presented. The method allows us to optimize multiple model parameters using a multivariate evaluation by comparing simulation results with field data based on objective, well-defined optimization variables. With these variables the simulation–observation correspondence is determined, and adjusted output parameter distributions representing optimal parameter combinations are found.

A large number of simulation runs are performed and for each parameter combination Θ = {μ, ξ, e_b } a set of simulated optimization variables X = {r, T, F, u _max, d, G} is determined. Parameter combinations with high correspondence are identified by analyzing the correspondence between simulated and observed optimization variables using the scalar metric α(X). A selection rule based on a correspondence limit α _lim is introduced and linked to a design event correspondence level α _design in a consistent manner. Parameter frequency distributions Ω_Θ are derived and analyzed statistically (e.g. to determine quantiles or bounds for the model parameters). Violine plots, which allow an intuitive interpretation of the parameter distributions (e.g. to identify multiple distribution maxima), are utilized for visualization. Additionally, an extensive sensitivity analysis allows for linking model parameters and simulation outcome and determining their predictive importance. For the investigated event, the statistical evaluation of the adjusted output parameter distributions showed a clear peak for the Coulomb friction parameter μ _25% = 0.24 < μ < μ _75% = 0.26 and the erosion energy parameter e _b,25% = 8825m² s⁻² < e_b < e _b,75% = 13 925 m² s⁻². Moreover these peaks coincide with the parameter values of maximum correspondence and , indicating high information reliability. For the turbulent friction parameter ξ a lower bound ξ > ξ _min = 7500 m s⁻², but no clear peak was identified, i.e. the parameter value of maximum correspondence is slightly larger than the 75% quantile value ξ _75% = 13 925ms⁻². This means that the optimal value of is some arbitrary value larger than ξ _min. However, for ξ values in this range, the magnitude of the turbulent friction diminishes, making its existence questionable, which is in agreement with other observations (Ancey and Meunier, 2004). Compared to prior optimization approaches, the optimal values of the turbulent friction appear to be about one order of magnitude larger (0.5–1.5 × 10⁻³ m s⁻² → 0.5–1.5 × 10⁴ m s⁻²). However, care has to be taken with this comparison, since in other studies entrainment or curvature effects (that introduce additional velocity-dependent friction and thus may have a significant influence on the effective values of the turbulent friction coefficient; cf. Fischer and others, 2012) were partly disregarded. Single parameters cannot be exchanged between different models due to differences in the model implementation. The fact that lower values for the turbulent friction coefficient ξ (i.e. higher friction) appear as high-correspondence solutions when leaving out the maximum velocity u _max as optimization variable is in correspondence with prior studies and indicates that lower ξ values lead to avalanche velocities that are too low (as previously noted by Gubler, 1987; Fischer and others, 2014; Gauer, 2014).

At this point, the advantage of adjusted parameter distributions over singular parameter sets should be highlighted. Statistical information is a major topic in modern engineering design. For example, the upper limit of a 90% confidence interval is usually used as a characteristic value for an action such as impact pressure in engineering codes. The derived parameter distributions include the total model and parameter uncertainties, which are related to a certain deviation of the design event. Thus predictive ensemble simulations are possible and can be used to determine confidence intervals for impact pressures or runouts, i.e. towards a conceptual approach (Meunier and Ancey, 2004) with operational models in 3-D terrain. Furthermore the combination of parameter distributions rather than singular parameter values is indispensable in order to consider the full spectrum of multi-event or multipath analyses.

With different examples we highlight the importance of the multivariate approach. Decreasing the size of the optimization variable set significantly reduces the information value of the adjusted parameter distributions. To adapt the set of optimization variables may be crucial when parameter distributions for different questions or applications have to be determined (e.g., for dam planning, an accurate flow velocity is more important than an accurate runout). The importance of each optimization variable varies for the different model parameters and is directly linked to the results of the sensitivity analysis. For example, the optimization variable of maximum velocity u _max is very important to increase the information value of the turbulent friction parameter distribution Ω _ξ but only slightly influences the distribution of the Coulomb friction Ω _μ . This is also reflected by the fact that the parameter μ is linked to many other optimization variables. The influence of the correspondence limit α _lim is studied and the related statistical stability is investigated.

One should note that the presented outcomes may change for other design event definitions, other avalanche paths and may not be transferable to flow models of the same family, or their implementation. Furthermore model parameters may not be constant but may vary in time and space, i.e. for different flow regimes and along the avalanche path. However, the strength of this optimization concept is the possibility that it might be adapted to multi-event or multipath analyses, or to other flow models and their related parameters, and it handles reduced or extended sets of optimization variables, i.e. more or less prior information.