1. Introduction
During the last glacial cycle the European Alps were covered by a large glacier network with the ice flow direction confined by the underlying topography, a so-called icefield. The glacier extent during this cycle is best known at the Last Glacial Maximum (LGM), 24 000 years before present (Ivy-Ochs and others, Reference Ivy-Ochs2008; Preusser and others, Reference Preusser, Graf, Keller, Krayss and Schlüchter2011). Based on terminal moraines and erratic boulders it was possible to reconstruct the former ice extent reached by the Alpine Icefield (AlpIF) at the LGM (Benz-Meier, Reference Benz-Meier2003; Bini and others, Reference Bini2009; Coutterand, Reference Coutterand2010; Ehlers and others, Reference Ehlers, Gibbard and Hughes2011). Further, trimlines were interpreted as the maximum ice surface elevation reached during the LGM (Florineth, Reference Florineth1998; Florineth and Schlüchter, Reference Florineth and Schlüchter1998; Benz-Meier, Reference Benz-Meier2003; Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004; Bini and others, Reference Bini2009; Coutterand, Reference Coutterand2010). Current geomorphological reconstructions portray the AlpIF as a vast icefield with several large piedmont lobes, abundant nunataks and ice flow directions predominantly constrained by the bedrock topography (Florineth, Reference Florineth1998; Florineth and Schlüchter, Reference Florineth and Schlüchter1998; Benz-Meier, Reference Benz-Meier2003; Kelly and others, Reference Kelly, Buoncristiani and Schlüchter2004; Bini and others, Reference Bini2009; Coutterand, Reference Coutterand2010).
By contrast, recent ice flow modelling studies depict the AlpIF at the LGM as a thick ice cap/ice sheet (Becker and others, Reference Becker, Seguinot, Jouvet and Funk2016, Reference Becker, Funk, Schlüchter and Hutter2017; Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018; Seguinot and others, Reference Seguinot2018). While the reconstructed maximum ice extent can be matched fairly well, the models produce ice thicknesses much greater than suggested by geomorphological evidence, about 500 m thicker in the valley part of the Rhine Glacier (Becker and others, Reference Becker, Seguinot, Jouvet and Funk2016), and 800–861 m thicker in the valley part of the Rhone Glacier (Becker and others, Reference Becker, Funk, Schlüchter and Hutter2017; Seguinot and others, Reference Seguinot2018). Only the modelling study by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) is able to match the reconstructed ice surface elevation. The maximum ice thickness reconstructions in the European Alps are mainly inferred from trimline reconstructions which are known within 100 m and only exist at few mountainsides in the valley part of the AlpIF (Florineth, Reference Florineth1998; Florineth and Schlüchter, Reference Florineth and Schlüchter1998). This range of uncertainty is much smaller than the ice thickness overestimations found by ice flow modelling, making the overestimated ice thicknesses significant. Therefore, the interpretation of trimlines as a former maximum ice surface elevation has been questioned and it was hypothesized that trimlines correspond instead to the transition between warm- and cold-based ice (Coutterand, Reference Coutterand2010; Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018; Seguinot and others, Reference Seguinot2018). However, no geomorphological evidence from the Alps supporting this idea has been presented so far.
These modelling studies have been performed with two kinds of ice flow models. Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) used a sophisticated model based on the Stokes equations, called Elmer/Ice (Gagliardini and others, Reference Gagliardini2013), which is capable of adequately reproducing the dynamics of ice within steep terrain, however, at high computational costs. Thus, this model cannot be used to simulate long timescales such as a full glacial cycle. By contrast, Becker and others (Reference Becker, Seguinot, Jouvet and Funk2016), Becker and others (Reference Becker, Funk, Schlüchter and Hutter2017), Jouvet and others (Reference Jouvet, Seguinot, Ivy-Ochs and Funk2017) and Seguinot and others (Reference Seguinot2018) have used a model based on simplified mechanics deduced from the Stokes equations that is capable of simulating the ice dynamics of the entire Alps over the last 120 000 years (Seguinot and others, Reference Seguinot2018). More precisely, they have used the Parallel Ice Sheet Model (PISM, Bueler and Brown, Reference Bueler and Brown2009; PISM Authors, 2019), a so-called hybrid ice-sheet/ice stream model that relies on the shallow ice approximation (SIA, Hutter, Reference Hutter1983) and the shallow shelf approximation (SSA, Weis and others, Reference Weis, Greve and Hutter1999) to describe horizontal shearing and basal sliding, respectively (Bueler and Brown, Reference Bueler and Brown2009). While the SIA is suitable for describing the horizontal shear deformation of vast continental ice sheets with negligible sliding, the SSA is suitable for describing plug-like flow as found in ice shelves or ice streams where sliding dominates the horizontal shearing. The SIA has proved its worth for modelling the ice dynamics within ice sheets, when used with coarse horizontal resolution (>10 km) (e.g. Greve, Reference Greve1997). Using such resolutions, the underlying assumptions for the SIA and the SSA are typically fulfilled, i.e., shallowness of the ice and small ice surface and bedrock slopes. However, higher model resolution (<10 km) is necessary for resolving steep and complex terrain where the higher order stress gradient terms neglected in the SIA and the SSA become more important. SIA models have been assessed several times using Stokes models (e.g. Hindmarsh, Reference Hindmarsh2004; Le Meur and others, Reference Le Meur, Gagliardini, Zwinger and Ruokolainen2004; Leysinger Vieli and Gudmundsson, Reference Leysinger Vieli and Gudmundsson2004; Pattyn and others, Reference Pattyn2008; Adhikari and Marshall, Reference Adhikari and Marshall2013; Brædstrup and others, Reference Brædstrup, Egholm, Ugelvig and Pedersen2016; Seddik and others, Reference Seddik, Greve, Zwinger and Sugiyama2017). However, to our knowledge, the applicability of the hybrid scheme at icefields has not yet been assessed in a similar way. Despite this, the PISM hybrid model has been used repeatedly to simulate the ice dynamics of icefields, not only within the European Alps but also within other mountain ranges (e.g. Golledge and others, Reference Golledge2012; Ziemen and others, Reference Ziemen2016; Yan and others, Reference Yan, Owen, Wang and Zhang2018). Another issue with high-resolution simulations employing the SIA within steep and complex terrain such as fjords or valleys is that high surface gradients can occur between adjacent grid cells resulting in high SIA shearing velocities. These require extremely small time steps to maintain numerical stability, which leads to an increase in computational time (PISM Authors, 2019). These high velocities increase the chance that more than the entire ice of a grid cell is drained within one time step, leading to mass conservation issues (Schäfer and Le Meur, Reference Schäfer and Le Meur2007; Jarosch and others, Reference Jarosch, Schoof and Anslow2013). To improve computational efficiency, PISM uses a scheme introduced by Schoof (Reference Schoof2003) that limits the SIA ice flux in steep and complex terrain. However, it is currently not understood how this method of limiting SIA ice fluxes in mountainous topography affects the ice dynamics.
Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) recently applied a Stokes model to the Rhine Glacier, a large north-central part of the AlpIF, during the LGM (Fig. 1). This study aims to remedy this situation by assessing model results obtained with hybrid mechanics (PISM 0.7.3) against Stokes mechanics (Elmer/Ice 7.0) when applied to icefields. Their work offers a unique opportunity for a comparison study with the PISM hybrid model, using the Elmer/Ice simulation as Stokes reference. We run PISM using a setup as similar as possible to the one described in Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), and compare the simulations of the two ice flow models in terms of horizontal shearing speeds, sliding speeds, ice thickness and basal temperatures. Further, we test the influence of the SIA ice-flux limiter scheme implemented in PISM on the ice flow at two different horizontal resolutions.

Fig. 1. Modelled ice thickness of the Rhine Glacier by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). The numbers indicate the Rhine Glacier Piedmont Lobe (1), the Linth/Limmat Piedmont Lobe (2) and the main Rhine Valley in the icefield sector (3). The Rhine Glacier diffluence at Sargans is also indicated.
The paper is outlined as follows. In Section 2 the two ice flow models are described with an emphasis on similarities and differences as well as on the experimental setups. Section 3 presents the numerical experiments and the model results. Section 4 discusses how PISM performs compared to Elmer/Ice, the limits of the hybrid formulation for modelling icefields as well as implications for previous studies employing PISM in the European Alps.
2. Methods and data
For comparison purposes, we apply PISM to the Rhine Glacier during the LGM by closely following the Elmer/Ice model setup of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). PISM and Elmer/Ice are both three-dimensional models that simulate ice flow, ice temperature and surface mass balance. Analogously to Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), we also use the present-day bedrock topography. The model is initialized based on the geomorphologically reconstructed ice thickness of the Rhine Glacier from Benz-Meier (Reference Benz-Meier2003) and run for 3262 years. While Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) interpolated the input dataset onto an unstructured grid with a mean horizontal resolution of ~0.5 km, we interpolate the same data to a regular grid with a horizontal resolution of $1$![]() and $2\,$
and $2\,$![]() km. For PISM, we also use the elevation-dependent surface mass-balance parametrization of the ‘S1’ setup of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) where the equilibrium line altitude (ELA) lies at 1200 m above sea level. The ablation gradient is 1 m a$^{-1}\,$
km. For PISM, we also use the elevation-dependent surface mass-balance parametrization of the ‘S1’ setup of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) where the equilibrium line altitude (ELA) lies at 1200 m above sea level. The ablation gradient is 1 m a$^{-1}\,$![]() km−1 whereas the accumulation gradient is 0.25 m a$^{-1}\,$
km−1 whereas the accumulation gradient is 0.25 m a$^{-1}\,$![]() km−1. The accumulation rate is capped at 0.26 m a−1. To model the ice temperature, PISM uses an enthalpy model (Aschwanden and others, Reference Aschwanden, Bueler, Khroulev and Blatter2012) with a constant vertical resolution of 50 m. By contrast, Elmer/Ice solves the heat equation with the constraints that the ice temperature is less or equal to the pressure melting point (Gagliardini and others, Reference Gagliardini2013) using 16 vertical layers with a finer resolution near the glacier bed. Further, in both models the thermal boundary conditions of the ‘S1’ setup of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) are applied, namely the geothermal heat flux of Medici and Rybach (Reference Medici and Rybach1995) at the glacier bed and an elevation-dependent mean annual near surface air temperature at the glacier surface. The annual mean temperature at the ELA is taken as –12$^{\circ }$
km−1. The accumulation rate is capped at 0.26 m a−1. To model the ice temperature, PISM uses an enthalpy model (Aschwanden and others, Reference Aschwanden, Bueler, Khroulev and Blatter2012) with a constant vertical resolution of 50 m. By contrast, Elmer/Ice solves the heat equation with the constraints that the ice temperature is less or equal to the pressure melting point (Gagliardini and others, Reference Gagliardini2013) using 16 vertical layers with a finer resolution near the glacier bed. Further, in both models the thermal boundary conditions of the ‘S1’ setup of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) are applied, namely the geothermal heat flux of Medici and Rybach (Reference Medici and Rybach1995) at the glacier bed and an elevation-dependent mean annual near surface air temperature at the glacier surface. The annual mean temperature at the ELA is taken as –12$^{\circ }$![]() C with an elevation gradient of –6$^{\circ }$
C with an elevation gradient of –6$^{\circ }$![]() C km−1. In both models, the initial vertical ice temperature profiles are estimated from the near surface air temperature, the geothermal heat flux and the accumulation rate. Following Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), frictional heating at the base of the glacier is neglected everywhere. In the PISM simulations, we set the ice thickness at the boundary of the Rhine Glacier catchment equal to zero, whereas in Elmer/Ice the ice flux across this boundary is set to zero. Using different boundary conditions in the two models has very little influence on our results since only a very small part of the Rhine Glacier ice drains across the boundary in the PISM simulations.
C km−1. In both models, the initial vertical ice temperature profiles are estimated from the near surface air temperature, the geothermal heat flux and the accumulation rate. Following Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), frictional heating at the base of the glacier is neglected everywhere. In the PISM simulations, we set the ice thickness at the boundary of the Rhine Glacier catchment equal to zero, whereas in Elmer/Ice the ice flux across this boundary is set to zero. Using different boundary conditions in the two models has very little influence on our results since only a very small part of the Rhine Glacier ice drains across the boundary in the PISM simulations.
The way in which PISM and Elmer/Ice calculate ice velocity fields and displacement of mass is the key difference between the two models. In PISM, the evolution of the ice surface elevation H is described by:
where a is the mass balance and $\vec Q$![]() the two-dimensional ice flux in x and y directions. $\vec Q$
the two-dimensional ice flux in x and y directions. $\vec Q$![]() in PISM is equal to the sum of the SIA-induced flux $\vec Q_{{\rm SIA}}$
in PISM is equal to the sum of the SIA-induced flux $\vec Q_{{\rm SIA}}$![]() and the SSA-induced flux $\vec Q_{{\rm SSA}} = h \cdot \vec v_{{\rm s}}$
and the SSA-induced flux $\vec Q_{{\rm SSA}} = h \cdot \vec v_{{\rm s}}$![]() , where $\vec v_{{\rm s}}$
, where $\vec v_{{\rm s}}$![]() is the sliding velocity computed by the SSA and h the ice thickness. By contrast, Elmer/Ice calculates a three-dimensional velocity field from the Stokes equations and thus also considers the vertical component of the ice flow (Gagliardini and others, Reference Gagliardini2013; Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). Furthermore, Elmer/Ice employs the finite element method rather than the finite difference method used by PISM. We use the same sliding law for the SSA of PISM as in Elmer/Ice by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), namely:
is the sliding velocity computed by the SSA and h the ice thickness. By contrast, Elmer/Ice calculates a three-dimensional velocity field from the Stokes equations and thus also considers the vertical component of the ice flow (Gagliardini and others, Reference Gagliardini2013; Cohen and others, Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). Furthermore, Elmer/Ice employs the finite element method rather than the finite difference method used by PISM. We use the same sliding law for the SSA of PISM as in Elmer/Ice by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018), namely:
where $\vec \tau _{\rm b}$![]() is a vector of the basal shear stress components, $C_0=1000\,$
is a vector of the basal shear stress components, $C_0=1000\,$![]() Pa a m−1 is the sliding parameter for temperate-based ice and $C_1=100,000\,$
Pa a m−1 is the sliding parameter for temperate-based ice and $C_1=100,000\,$![]() Pa a m−1 is the sliding parameter for cold-based ice. $C_1$
Pa a m−1 is the sliding parameter for cold-based ice. $C_1$![]() is used to suppress sliding where basal temperatures T are below the pressure melting point $T_{{\rm pmp}}$
is used to suppress sliding where basal temperatures T are below the pressure melting point $T_{{\rm pmp}}$![]() . The exponential in Eqn (2) serves to smooth the transition between cold-based and temperate-based ice with a sub-melting sliding parameter $\gamma = 2\,$
. The exponential in Eqn (2) serves to smooth the transition between cold-based and temperate-based ice with a sub-melting sliding parameter $\gamma = 2\,$![]() K. This kind of sliding law is not included in PISM 0.7.3 and, therefore, we implemented it ourselves. The SIA ice flux of PISM, $\vec Q_{{\rm SIA}}$
K. This kind of sliding law is not included in PISM 0.7.3 and, therefore, we implemented it ourselves. The SIA ice flux of PISM, $\vec Q_{{\rm SIA}}$![]() , is described by:
, is described by:
where D is the ice diffusivity resulting from the SIA,
E = 1 is the flow enhancement factor, $\rho _{{\rm i}}=917\,$![]() kg m−3 the density of ice, $g=9.81\,$
kg m−3 the density of ice, $g=9.81\,$![]() m s−2 the gravitational acceleration and n = 3 the Glen's flow law exponent, all having identical values in both models. The temperature-dependent rate factor $A(T)$
m s−2 the gravitational acceleration and n = 3 the Glen's flow law exponent, all having identical values in both models. The temperature-dependent rate factor $A(T)$![]() follows in all cases the Arrhenius relation described in Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). The parameter θ is a scaling factor for the SIA proposed by Schoof (Reference Schoof2003) that takes values between zero and one. Using a multiple-scale expansion technique, Schoof (Reference Schoof2003) has shown that the effect of higher order stresses that arise when ice flows over a bumpy bedrock can be parametrized by multiplying a factor θ with the classical SIA ice flux. However, the primary motivation for using the method of Schoof (Reference Schoof2003), hereafter called Schoof scheme, in PISM is to reduce and smooth spikes in the diffusivity term (Eqn (4)) induced by locally steep terrain. This allows to use longer time steps and therefore enhances the computational speed and reduces mass conservation errors (PISM Authors, 2019). The Schoof scheme assumes that the typical length scale on which the topography changes is much greater than the ice thickness but much less than the lateral extent of the ice body – an assumption that is not always fulfilled in the case of the LGM Rhine Glacier or other Alpine glaciers and icefields. A further critical assumption is that the bedrock topography must nowhere protrude above the ice surface, i.e., the Schoof scheme is not valid near nunataks or near the glacier margin (Schoof, Reference Schoof2003). The Schoof scheme computes a smoothed version $b_{\rm s}$
follows in all cases the Arrhenius relation described in Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). The parameter θ is a scaling factor for the SIA proposed by Schoof (Reference Schoof2003) that takes values between zero and one. Using a multiple-scale expansion technique, Schoof (Reference Schoof2003) has shown that the effect of higher order stresses that arise when ice flows over a bumpy bedrock can be parametrized by multiplying a factor θ with the classical SIA ice flux. However, the primary motivation for using the method of Schoof (Reference Schoof2003), hereafter called Schoof scheme, in PISM is to reduce and smooth spikes in the diffusivity term (Eqn (4)) induced by locally steep terrain. This allows to use longer time steps and therefore enhances the computational speed and reduces mass conservation errors (PISM Authors, 2019). The Schoof scheme assumes that the typical length scale on which the topography changes is much greater than the ice thickness but much less than the lateral extent of the ice body – an assumption that is not always fulfilled in the case of the LGM Rhine Glacier or other Alpine glaciers and icefields. A further critical assumption is that the bedrock topography must nowhere protrude above the ice surface, i.e., the Schoof scheme is not valid near nunataks or near the glacier margin (Schoof, Reference Schoof2003). The Schoof scheme computes a smoothed version $b_{\rm s}$![]() of the original bedrock $b_0$
of the original bedrock $b_0$![]() over a length scale λ as follows:
over a length scale λ as follows:
Following Schoof (Reference Schoof2003), θ is calculated with:

where n is the Glen's flow law exponent and $\widetilde {h}$![]() is the difference between the ice surface elevation H and the smoothed bedrock, i.e. the ice thickness relative to $b_{\rm s}$
is the difference between the ice surface elevation H and the smoothed bedrock, i.e. the ice thickness relative to $b_{\rm s}$![]() :
:
The residual bedrock topography, $b_{\rm r}$![]() , is given by:
, is given by:
If θ is evaluated in areas where the ratio ${b_{\rm r}}/{\widetilde {h}}$![]() is close or equal to one (large residual bedrock topography compared to ice thickness), Eqn (6) yields a θ close or even equal to zero. This is the case for example near nunataks or at the glacial margin in valleys. As a consequence, the ice flux due to horizontal shear deformation is drastically reduced or even shut down completely in such situations. By contrast, if θ is evaluated in areas where the ratio ${b_{\rm r}}/{\widetilde {h}}$
is close or equal to one (large residual bedrock topography compared to ice thickness), Eqn (6) yields a θ close or even equal to zero. This is the case for example near nunataks or at the glacial margin in valleys. As a consequence, the ice flux due to horizontal shear deformation is drastically reduced or even shut down completely in such situations. By contrast, if θ is evaluated in areas where the ratio ${b_{\rm r}}/{\widetilde {h}}$![]() is close to zero (small residual bedrock topography compared to ice thickness), Eqn (6) yields a θ close to one and Eqn (4) simplifies to the unweighted ice diffusivity. In practice, PISM calculates $\theta (x,y)$
is close to zero (small residual bedrock topography compared to ice thickness), Eqn (6) yields a θ close to one and Eqn (4) simplifies to the unweighted ice diffusivity. In practice, PISM calculates $\theta (x,y)$![]() with a fourth-order Taylor approximation of Eqn (6) to enhance computational efficiency. The smoothing range is commonly taken as $\lambda =5\,$
with a fourth-order Taylor approximation of Eqn (6) to enhance computational efficiency. The smoothing range is commonly taken as $\lambda =5\,$![]() km which is the value recommended by Schoof (Reference Schoof2003) for ice sheets and used by default in PISM. At a resolution of $1\,$
km which is the value recommended by Schoof (Reference Schoof2003) for ice sheets and used by default in PISM. At a resolution of $1\,$![]() km ($2\,$
km ($2\,$![]() km), this corresponds to a window of $11\times 11$
km), this corresponds to a window of $11\times 11$![]() ($6\times 6$
($6\times 6$![]() ) grid cells. Using a smaller λ results in less smoothing in Eqn (5) and consequently a residual bedrock topography $b_{\rm r}$
) grid cells. Using a smaller λ results in less smoothing in Eqn (5) and consequently a residual bedrock topography $b_{\rm r}$![]() closer to zero (Eqn (8)). This way, the ratio between residual bedrock topography and ice thickness gets closer to zero. In turn, this leads to greater values for θ and therefore a diminished SIA flux reduction. Note that the Schoof scheme vanishes if λ is set to zero. In that case, the smoothed bedrock $b_{\rm s}$
closer to zero (Eqn (8)). This way, the ratio between residual bedrock topography and ice thickness gets closer to zero. In turn, this leads to greater values for θ and therefore a diminished SIA flux reduction. Note that the Schoof scheme vanishes if λ is set to zero. In that case, the smoothed bedrock $b_{\rm s}$![]() is identical to the original bedrock $b_0$
is identical to the original bedrock $b_0$![]() , which results in Eqn (6) yielding $\theta =1$
, which results in Eqn (6) yielding $\theta =1$![]() everywhere as the residual bedrock topography $b_{\rm r}$
everywhere as the residual bedrock topography $b_{\rm r}$![]() is always zero.
is always zero.
3. Results
In this section, we present the results obtained with PISM and Elmer/Ice, the latter being taken directly from Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) and used as reference simulation. For this purpose, we initialize PISM with the geomorphologically reconstructed Rhine Glacier and run the model for 3262 years with an energy and surface mass balance forcing constant in time at a horizontal resolution of $1$![]() and $2\,$
and $2\,$![]() km. To compare the PISM hybrid results with the Elmer/Ice Stokes results, we linearly interpolate the latter output to the regular grid used by PISM. We perform two simulations with PISM for each model resolution: one with the recommended value $\lambda =5\,$
km. To compare the PISM hybrid results with the Elmer/Ice Stokes results, we linearly interpolate the latter output to the regular grid used by PISM. We perform two simulations with PISM for each model resolution: one with the recommended value $\lambda =5\,$![]() km for the Schoof scheme, and one with $\lambda =1\,$
km for the Schoof scheme, and one with $\lambda =1\,$![]() km ($\lambda =2\,$
km ($\lambda =2\,$![]() km for the simulation using a horizontal resolution of $2\,$
km for the simulation using a horizontal resolution of $2\,$![]() km), which results in the smallest possible smoothing window of $3\times 3$
km), which results in the smallest possible smoothing window of $3\times 3$![]() grid cells and thus the smallest possible SIA flux reduction. For the detailed analysis, we use the $1\,$
grid cells and thus the smallest possible SIA flux reduction. For the detailed analysis, we use the $1\,$![]() km simulations, whereas the $2\,$
km simulations, whereas the $2\,$![]() km simulations are only used in Sections 3.5 and 4.5 to investigate how the Schoof scheme interacts with model resolution. Running PISM without the Schoof scheme is not considered here because such a setup does not conserve mass reliably. The detailed comparison of the model results is carried out at the model year 3262, corresponding to the final state of the Elmer/Ice simulation of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). Among the two PISM simulations using a horizontal resolution of $1 \,$
km simulations are only used in Sections 3.5 and 4.5 to investigate how the Schoof scheme interacts with model resolution. Running PISM without the Schoof scheme is not considered here because such a setup does not conserve mass reliably. The detailed comparison of the model results is carried out at the model year 3262, corresponding to the final state of the Elmer/Ice simulation of Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018). Among the two PISM simulations using a horizontal resolution of $1 \,$![]() km and Elmer/Ice, the ice volume remains almost constant during the first 2000 years but starts to grow afterwards in both PISM simulations, especially in the PISM simulation with $\lambda =5\,$
km and Elmer/Ice, the ice volume remains almost constant during the first 2000 years but starts to grow afterwards in both PISM simulations, especially in the PISM simulation with $\lambda =5\,$![]() km (Fig. 2a). In all three simulations, the Rhine Glacier Piedmont Lobe retreats at the beginning and starts to slowly re-advance shortly after the year 2500 (Fig. 2b). The retreat is notably larger in PISM with $\lambda =5\,$
km (Fig. 2a). In all three simulations, the Rhine Glacier Piedmont Lobe retreats at the beginning and starts to slowly re-advance shortly after the year 2500 (Fig. 2b). The retreat is notably larger in PISM with $\lambda =5\,$![]() km than in PISM with $\lambda =1 \,$
km than in PISM with $\lambda =1 \,$![]() km and Elmer/Ice. The quick rise in ice covered area at the beginning of each simulations is due to nunataks that are ice-free in the initialized state but become ice covered in all three model runs. The mean ice thickness of Elmer/Ice remains almost constant over the entire 3262 years whereas PISM with $\lambda =1\,$
km and Elmer/Ice. The quick rise in ice covered area at the beginning of each simulations is due to nunataks that are ice-free in the initialized state but become ice covered in all three model runs. The mean ice thickness of Elmer/Ice remains almost constant over the entire 3262 years whereas PISM with $\lambda =1\,$![]() km thickens slightly (Fig. 2c). In contrast, PISM with $\lambda =5\,$
km thickens slightly (Fig. 2c). In contrast, PISM with $\lambda =5\,$![]() km thickens significantly over the modelled period. Elmer/Ice appears to be very close to an equilibrium state in the year 3262, whereas PISM with $\lambda =1\,$
km thickens significantly over the modelled period. Elmer/Ice appears to be very close to an equilibrium state in the year 3262, whereas PISM with $\lambda =1\,$![]() km and especially PISM with $\lambda =5\,$
km and especially PISM with $\lambda =5\,$![]() km show positive mass trends (Fig. 2). After 3262 years, Elmer/Ice depicts a Rhine Glacier with a glacierized area of 13,291 km2, a volume of 5615 km3, and thus a mean ice thickness of 422 m (Table 1). The PISM Rhine Glacier with $\lambda =5\,$
km show positive mass trends (Fig. 2). After 3262 years, Elmer/Ice depicts a Rhine Glacier with a glacierized area of 13,291 km2, a volume of 5615 km3, and thus a mean ice thickness of 422 m (Table 1). The PISM Rhine Glacier with $\lambda =5\,$![]() km has a glacierized area 18% smaller than that of Elmer/Ice. This is mostly due to the fact that the Linth/Limmat and the Rhine Glacier Piedmont Lobes are significantly smaller (e.g. Fig. 3b). Simultaneously, PISM with $\lambda =5\,$
km has a glacierized area 18% smaller than that of Elmer/Ice. This is mostly due to the fact that the Linth/Limmat and the Rhine Glacier Piedmont Lobes are significantly smaller (e.g. Fig. 3b). Simultaneously, PISM with $\lambda =5\,$![]() km yields an ice volume 32% greater than the Elmer/Ice one. As a consequence, the mean ice thickness is overestimated by 255 m or 60%. Using PISM with $\lambda =1\,$
km yields an ice volume 32% greater than the Elmer/Ice one. As a consequence, the mean ice thickness is overestimated by 255 m or 60%. Using PISM with $\lambda =1\,$![]() km yields a glacierized area that agrees well with Elmer/Ice, overestimating it only by 2%. This small area overestimation can be traced, for the most part, to the Rhine Glacier Piedmont Lobe that extends somewhat further to the east (e.g. Fig. 3c). The Rhine Glacier ice volume modelled by PISM with $\lambda =1\,$
km yields a glacierized area that agrees well with Elmer/Ice, overestimating it only by 2%. This small area overestimation can be traced, for the most part, to the Rhine Glacier Piedmont Lobe that extends somewhat further to the east (e.g. Fig. 3c). The Rhine Glacier ice volume modelled by PISM with $\lambda =1\,$![]() km is 15% greater than that of Elmer/Ice. Similarly, the mean ice thickness obtained with PISM with $\lambda =1\,$
km is 15% greater than that of Elmer/Ice. Similarly, the mean ice thickness obtained with PISM with $\lambda =1\,$![]() km is only 56 m or 13% greater than in Elmer/Ice.
km is only 56 m or 13% greater than in Elmer/Ice.

Fig. 2. Temporal evolution of ice volume (a), ice covered area (b) and mean ice thickness (c) using a horizontal resolution of $1\,$![]() km. The solid line represents the Elmer/Ice simulation, the dashed line PISM using $\lambda =5\,$
km. The solid line represents the Elmer/Ice simulation, the dashed line PISM using $\lambda =5\,$![]() km and the dotted line PISM using $\lambda =1\,$
km and the dotted line PISM using $\lambda =1\,$![]() km.
km.

Fig. 3. Shearing speeds of the $1\,$![]() km simulations 3262 years after initialization modelled with Elmer/Ice (a), PISM with $\lambda =5\,$
km simulations 3262 years after initialization modelled with Elmer/Ice (a), PISM with $\lambda =5\,$![]() km (b) and PISM with $\lambda =1\,$
km (b) and PISM with $\lambda =1\,$![]() km (c). Gray indicates areas where shearing speeds are exactly zero. The black line represents the ice extent produced by Elmer/Ice.
km (c). Gray indicates areas where shearing speeds are exactly zero. The black line represents the ice extent produced by Elmer/Ice.
Table 1. Glacierized area (A), ice volume (V) and mean ice thickness (H) obtained with Elmer/Ice and PISM 3262 years after initialization for the simulations using a horizontal resolution of $1\,{\rm km}$![]()

The percentage numbers give the deviation from Elmer/Ice.
3.1. Shearing speeds
The shearing speeds (surface speed minus sliding speed) modelled by Elmer/Ice are mostly between 0.1 and 60 m a−1 (Fig. 3a), whereas shearing speeds modelled by PISM range between 0 and 120 m a−1 (Figs 3b, c). In Elmer/Ice, the high shearing speeds are concentrated in the main Rhine Valley and the smaller tributary valleys. Outside the valleys the shearing speeds are small with values between 0.1 and 1 m a−1. At the Rhine Glacier Piedmont Lobe, the Elmer/Ice shearing speeds continuously decrease towards the glacial margin in all directions. By contrast, the modelled shearing speeds in PISM with $\lambda =5\,$![]() km are zero in most of the icefield sector of the Rhine Glacier (Fig. 3b). Significant shearing speeds occur only at the lower main Rhine Valley and at the Rhine Glacier Piedmont Lobe. Using PISM with $\lambda =1\,$
km are zero in most of the icefield sector of the Rhine Glacier (Fig. 3b). Significant shearing speeds occur only at the lower main Rhine Valley and at the Rhine Glacier Piedmont Lobe. Using PISM with $\lambda =1\,$![]() km the shearing speed pattern follows the large and most smaller valleys, similar to Elmer/Ice (Fig. 3c). At the ridges next to the alpine valleys the shearing speeds are smaller than 0.1 m a−1 or zero which is significantly less than in Elmer/Ice. By contrast, the shearing speeds in the centre of the main Rhine Valley are about twice as large in PISM with $\lambda =1\,$
km the shearing speed pattern follows the large and most smaller valleys, similar to Elmer/Ice (Fig. 3c). At the ridges next to the alpine valleys the shearing speeds are smaller than 0.1 m a−1 or zero which is significantly less than in Elmer/Ice. By contrast, the shearing speeds in the centre of the main Rhine Valley are about twice as large in PISM with $\lambda =1\,$![]() km than in Elmer/Ice. Thus PISM with $\lambda =1\,$
km than in Elmer/Ice. Thus PISM with $\lambda =1\,$![]() km captures the shearing speed pattern in the icefield sector but overestimates the high speeds and underestimates the low speeds there. At the western end of the Rhine Glacier Piedmont Lobe, shearing speeds obtained with PISM using $\lambda =1\,$
km captures the shearing speed pattern in the icefield sector but overestimates the high speeds and underestimates the low speeds there. At the western end of the Rhine Glacier Piedmont Lobe, shearing speeds obtained with PISM using $\lambda =1\,$![]() km and with Elmer/Ice are very similar in magnitude and decrease continuously towards the lobe margin. However, to the east and north the shearing speeds in PISM using $\lambda =1\,$
km and with Elmer/Ice are very similar in magnitude and decrease continuously towards the lobe margin. However, to the east and north the shearing speeds in PISM using $\lambda =1\,$![]() km suddenly drop to 0.1–1 m a−1, which is not the case for Elmer/Ice. For the two PISM simulations, the spatial distributions of the SIA ice flux limiter θ are shown in Figure 4. Using PISM with $\lambda =5\,$
km suddenly drop to 0.1–1 m a−1, which is not the case for Elmer/Ice. For the two PISM simulations, the spatial distributions of the SIA ice flux limiter θ are shown in Figure 4. Using PISM with $\lambda =5\,$![]() km, θ is often zero in the alpine region of the Rhine Glacier. Non-zero values for θ occur but are barely greater than 0.4. A pattern following the small or large valleys is hardly visible. θ is close to one at the centre of the Rhine Glacier Piedmont Lobe but takes smaller values towards the lobe edge. In PISM with $\lambda =1\,$
km, θ is often zero in the alpine region of the Rhine Glacier. Non-zero values for θ occur but are barely greater than 0.4. A pattern following the small or large valleys is hardly visible. θ is close to one at the centre of the Rhine Glacier Piedmont Lobe but takes smaller values towards the lobe edge. In PISM with $\lambda =1\,$![]() km, θ values are close to one, not only at the Rhine Glacier Piedmont Lobe but also in some major alpine valleys (Fig. 4b). At the ridges next to the alpine valleys, θ is smaller than 0.2 and often also equal to zero as found in the PISM run using $\lambda =5\,$
km, θ values are close to one, not only at the Rhine Glacier Piedmont Lobe but also in some major alpine valleys (Fig. 4b). At the ridges next to the alpine valleys, θ is smaller than 0.2 and often also equal to zero as found in the PISM run using $\lambda =5\,$![]() km.
km.

Fig. 4. Spatial distribution of θ obtained with PISM using a horizontal resolution of $1\,$![]() km and $\lambda =5\,$
km and $\lambda =5\,$![]() km (a) and $\lambda =1\,$
km (a) and $\lambda =1\,$![]() km (b) 3262 years after initialization. Red indicates areas where θ is exactly zero. The black line represents the ice extent produced by Elmer/Ice.
km (b) 3262 years after initialization. Red indicates areas where θ is exactly zero. The black line represents the ice extent produced by Elmer/Ice.
3.2. Sliding speeds
The modelled sliding speeds of Elmer/Ice and PISM are mostly between 0.1 and 100 m a−1 (Fig. 5). The highest speeds occur in the main Rhine Valley and the piedmont lobes. In the icefield sector of the Rhine Glacier, both PISM and Elmer/Ice simulations yield similar results in terms of sliding speeds and pattern (Fig. 5). One exception is the diffluence of the Rhine Glacier at Sargans that is produced by Elmer/Ice and PISM with $\lambda =1\,$![]() km, but only very weak in the PISM simulation with $\lambda =5\,$
km, but only very weak in the PISM simulation with $\lambda =5\,$![]() km. Further, sliding speeds in the upper main Rhine Valley are larger in the PISM simulation with $\lambda =5\,$
km. Further, sliding speeds in the upper main Rhine Valley are larger in the PISM simulation with $\lambda =5\,$![]() km than in Elmer/Ice (Fig. 5). The most notable feature is the 50 km long fast-flowing strip orientated in a north-eastward direction. Figures 6a, b compare the sliding speeds of Elmer/Ice with PISM using $\lambda =5\,$
km than in Elmer/Ice (Fig. 5). The most notable feature is the 50 km long fast-flowing strip orientated in a north-eastward direction. Figures 6a, b compare the sliding speeds of Elmer/Ice with PISM using $\lambda =5\,$![]() km and PISM using $\lambda =1\,$
km and PISM using $\lambda =1\,$![]() km respectively at every grid cell with ice coverage. The majority of points clusters up near the diagonal, indicating that the modelled sliding speeds of both PISM runs correlate well with the Elmer/Ice ones over the entire range of modelled speeds (r = 0.79 for PISM with $\lambda =5\,$
km respectively at every grid cell with ice coverage. The majority of points clusters up near the diagonal, indicating that the modelled sliding speeds of both PISM runs correlate well with the Elmer/Ice ones over the entire range of modelled speeds (r = 0.79 for PISM with $\lambda =5\,$![]() km and r = 0.61 for PISM with $\lambda =1\,$
km and r = 0.61 for PISM with $\lambda =1\,$![]() km). This is particularly the case for sliding speeds greater than 10 m a−1 (Fig. 6). Cold-based sliding speeds are between 0.1 and 10 m a−1, while temperate sliding speeds are larger than 10 m a−1.
km). This is particularly the case for sliding speeds greater than 10 m a−1 (Fig. 6). Cold-based sliding speeds are between 0.1 and 10 m a−1, while temperate sliding speeds are larger than 10 m a−1.

Fig. 5. Sliding speeds of the $1\,$![]() km simulations 3262 years after initialization modelled with Elmer/Ice (a), PISM with $\lambda =5\,$
km simulations 3262 years after initialization modelled with Elmer/Ice (a), PISM with $\lambda =5\,$![]() km (b)and PISM with $\lambda =1\,$
km (b)and PISM with $\lambda =1\,$![]() km (c). The black line represents the ice extent produced by Elmer/Ice.
km (c). The black line represents the ice extent produced by Elmer/Ice.

Fig. 6. Sliding speeds of PISM using a resolution of $1\,$![]() km vs. Elmer/Ice sliding speeds for the two different setups of PISM: $\lambda =5\,$
km vs. Elmer/Ice sliding speeds for the two different setups of PISM: $\lambda =5\,$![]() km (a) and $\lambda =1\,$
km (a) and $\lambda =1\,$![]() km (b). Red indicates a temperate base and blue a cold base. Dark colours indicate a clustering of dots. The ideal agreement follows the dotted diagonal. The correlation is r=0.79 for $\lambda =5\,$
km (b). Red indicates a temperate base and blue a cold base. Dark colours indicate a clustering of dots. The ideal agreement follows the dotted diagonal. The correlation is r=0.79 for $\lambda =5\,$![]() km and r = 0.61 for $\lambda =1\,$
km and r = 0.61 for $\lambda =1\,$![]() km.
km.
3.3. Ice thickness deviation
Differences in ice thickness between Elmer/Ice and PISM are shown in Figure 7. PISM with $\lambda =5\,$![]() km produces an ice thickness 300–500 m larger than that of Elmer/Ice in the icefield sector of the Rhine Glacier, whereas the Limmat/Linth Lobe and the Rhine Glacier Piedmont Lobe are thinner and smaller than in Elmer/Ice (Fig. 7a). By contrast, the ice thickness of PISM with $\lambda =1\,$
km produces an ice thickness 300–500 m larger than that of Elmer/Ice in the icefield sector of the Rhine Glacier, whereas the Limmat/Linth Lobe and the Rhine Glacier Piedmont Lobe are thinner and smaller than in Elmer/Ice (Fig. 7a). By contrast, the ice thickness of PISM with $\lambda =1\,$![]() km agrees well with Elmer/Ice within $\pm\! 100\,$
km agrees well with Elmer/Ice within $\pm\! 100\,$![]() m in the icefield sector of the Rhine Glacier (Fig. 7b), while the Rhine Glacier Piedmont Lobe is 100–200 m thicker than in Elmer/Ice in most parts. The mean ice thicknesses of the three simulations and the deviation relative to Elmer/Ice are given in Table 1.
m in the icefield sector of the Rhine Glacier (Fig. 7b), while the Rhine Glacier Piedmont Lobe is 100–200 m thicker than in Elmer/Ice in most parts. The mean ice thicknesses of the three simulations and the deviation relative to Elmer/Ice are given in Table 1.

Fig. 7. Modelled ice thickness deviations of the $1\,$![]() km simulations between PISM with $\lambda =5\,$
km simulations between PISM with $\lambda =5\,$![]() km and Elmer/Ice (a) and between PISM with $\lambda =1\,$
km and Elmer/Ice (a) and between PISM with $\lambda =1\,$![]() km and Elmer/Ice (b) 3262 years after initialization. The black line represents the ice extent produced by Elmer/Ice.
km and Elmer/Ice (b) 3262 years after initialization. The black line represents the ice extent produced by Elmer/Ice.
3.4. Basal thermal regime
All three model runs depict the Rhine Glacier as a polythermal glacier (Fig. 8). The mountainous area is mostly cold-based whereas the main valleys are temperate. The extent of temperate ice in the upper main Rhine Valley is greater in the results obtained with PISM than with Elmer/Ice. Especially PISM with $\lambda =5\,$![]() km shows a much more extensive temperate area in the upper Rhine Valley part than Elmer/Ice (Fig. 8b). In all three model runs, the Rhine Glacier Piedmont Lobe is temperate in a central narrow strip that is orientated to the north-west and slightly below the pressure melting point towards the lobe margin (Fig. 8). The Elmer/Ice run additionally shows several small patches of temperate ice outside the narrow strip, which is not the case in the two PISM simulations. In PISM with $\lambda =1\,$
km shows a much more extensive temperate area in the upper Rhine Valley part than Elmer/Ice (Fig. 8b). In all three model runs, the Rhine Glacier Piedmont Lobe is temperate in a central narrow strip that is orientated to the north-west and slightly below the pressure melting point towards the lobe margin (Fig. 8). The Elmer/Ice run additionally shows several small patches of temperate ice outside the narrow strip, which is not the case in the two PISM simulations. In PISM with $\lambda =1\,$![]() km, a spot in the north of the Piedmont Lobe and the area towards the north-east are entirely temperate which is clearly not the case in Elmer/Ice. The basal temperatures of both PISM simulations are plotted against the Elmer/Ice ones in Figure 9. PISM with $\lambda =5\,$
km, a spot in the north of the Piedmont Lobe and the area towards the north-east are entirely temperate which is clearly not the case in Elmer/Ice. The basal temperatures of both PISM simulations are plotted against the Elmer/Ice ones in Figure 9. PISM with $\lambda =5\,$![]() km yields basal temperatures that are on average 1.5$^\circ$
km yields basal temperatures that are on average 1.5$^\circ$![]() C above the Elmer/Ice ones (Fig. 9a), whereas Elmer/Ice and PISM with $\lambda =1\,$
C above the Elmer/Ice ones (Fig. 9a), whereas Elmer/Ice and PISM with $\lambda =1\,$![]() km basal temperatures did not differ significantly, on average, at the Rhine Glacier (Fig. 9b). The correlation of basal temperatures of Elmer/Ice and PISM with $\lambda =5\,$
km basal temperatures did not differ significantly, on average, at the Rhine Glacier (Fig. 9b). The correlation of basal temperatures of Elmer/Ice and PISM with $\lambda =5\,$![]() km is r = 0.83 and for Elmer/Ice and PISM with $\lambda =1\,$
km is r = 0.83 and for Elmer/Ice and PISM with $\lambda =1\,$![]() km r = 0.90.
km r = 0.90.

Fig. 8. Basal temperatures of the $1\,$![]() km simulations 3262 years after initialization modelled by Elmer/Ice (a), PISM with $\lambda =5\,$
km simulations 3262 years after initialization modelled by Elmer/Ice (a), PISM with $\lambda =5\,$![]() km (b)and PISM with $\lambda =1\,$
km (b)and PISM with $\lambda =1\,$![]() km (c). Red indicates locations that are at the pressure melting point, i.e. temperate. The black line represents the ice extent produced by Elmer/Ice.
km (c). Red indicates locations that are at the pressure melting point, i.e. temperate. The black line represents the ice extent produced by Elmer/Ice.

Fig. 9. Basal temperatures modelled with PISM at a horizontal resolution of $1\,$![]() km with $\lambda =5\,$
km with $\lambda =5\,$![]() km (a) and $\lambda =1\,$
km (a) and $\lambda =1\,$![]() km (b) plotted against those modelled by Elmer/Ice. The solid black lines indicate corresponding linear regressions. The ideal agreement follows the dotted diagonal. The correlation is r = 0.83 for $\lambda =5\,$
km (b) plotted against those modelled by Elmer/Ice. The solid black lines indicate corresponding linear regressions. The ideal agreement follows the dotted diagonal. The correlation is r = 0.83 for $\lambda =5\,$![]() km and r = 0.90 for $\lambda =1\,$
km and r = 0.90 for $\lambda =1\,$![]() km.
km.
3.5. Using a coarser horizontal resolution
Running PISM with $\lambda =5\,$![]() km at a resolution of $2\,$
km at a resolution of $2\,$![]() km results in an ice volume 30% greater and a mean ice thickness 65% greater than in Elmer/Ice (Table 2). Further, the glacierized area is 21% smaller than in Elmer/Ice. This is due to the reduced extent of the Linth/Limmat and Rhine Glacier Piedmont Lobes (Fig. 10a). In the icefield sector of the Rhine Glacier, PISM with $\lambda =5\,$
km results in an ice volume 30% greater and a mean ice thickness 65% greater than in Elmer/Ice (Table 2). Further, the glacierized area is 21% smaller than in Elmer/Ice. This is due to the reduced extent of the Linth/Limmat and Rhine Glacier Piedmont Lobes (Fig. 10a). In the icefield sector of the Rhine Glacier, PISM with $\lambda =5\,$![]() km produces an ice thickness 300–500 m greater than Elmer/Ice (Fig. 10a). θ is zero in a significant portion of the icefield and hardly reaches values larger than 0.4 (Fig. 11a). θ reaches values close to one only at the Rhine Glacier Piedmont Lobe. Using PISM with $\lambda =2\,$
km produces an ice thickness 300–500 m greater than Elmer/Ice (Fig. 10a). θ is zero in a significant portion of the icefield and hardly reaches values larger than 0.4 (Fig. 11a). θ reaches values close to one only at the Rhine Glacier Piedmont Lobe. Using PISM with $\lambda =2\,$![]() km at a resolution of $2\,$
km at a resolution of $2\,$![]() km results in a glacierized area only 5% smaller than in Elmer/Ice and an ice volume 14% larger than in Elmer/Ice (Table 2). The mean ice thickness is overestimated by 21% compared to Elmer/Ice. Figure 10b indicates that the ice thickness is overestimated by 100–200 m in the major part of the icefield sector. θ is close to one at the Piedmont Lobes (Fig. 11b) but hardly reaches values larger than 0.8 in the alpine valleys. At the same time, θ is smaller than 0.2 and often zero at the mountains next to the main valleys.
km results in a glacierized area only 5% smaller than in Elmer/Ice and an ice volume 14% larger than in Elmer/Ice (Table 2). The mean ice thickness is overestimated by 21% compared to Elmer/Ice. Figure 10b indicates that the ice thickness is overestimated by 100–200 m in the major part of the icefield sector. θ is close to one at the Piedmont Lobes (Fig. 11b) but hardly reaches values larger than 0.8 in the alpine valleys. At the same time, θ is smaller than 0.2 and often zero at the mountains next to the main valleys.
Table 2. Glacierized area (A), ice volume (V) and mean ice thickness (H) obtained with Elmer/Ice and PISM 3262 years after initialization for the simulations using a horizontal resolution of $2\,{\rm km}$![]()

The percentage numbers give the deviation from Elmer/Ice.

Fig. 10. Modelled ice thickness deviations of the $2\,$![]() km simulations between PISM with $\lambda =5\,$
km simulations between PISM with $\lambda =5\,$![]() km and Elmer/Ice (a) and between PISM with $\lambda =2\,$
km and Elmer/Ice (a) and between PISM with $\lambda =2\,$![]() km and Elmer/Ice (b) 3262 years after initialization. The black line represents the ice extent modelled with Elmer/Ice.
km and Elmer/Ice (b) 3262 years after initialization. The black line represents the ice extent modelled with Elmer/Ice.
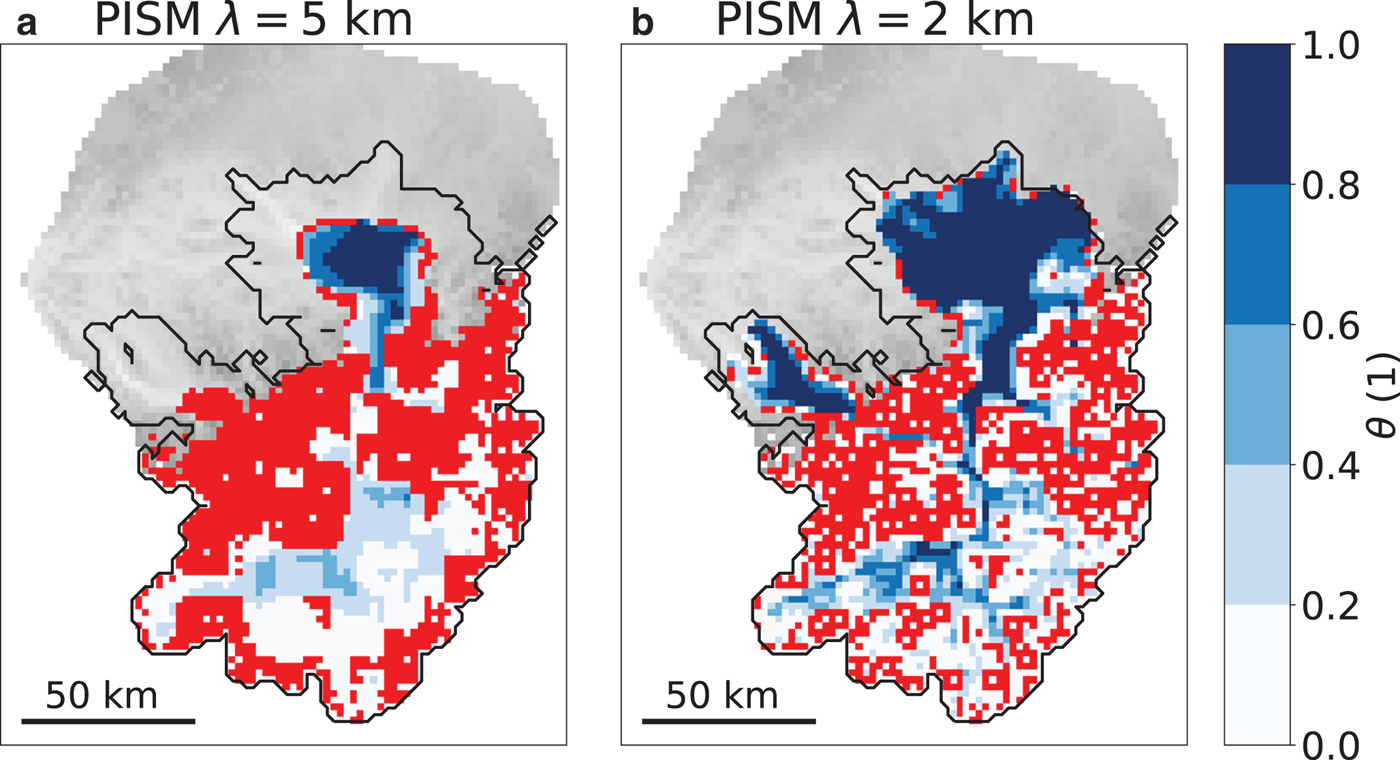
Fig. 11. Spatial distribution of θ obtained with PISM using a horizontal resolution of $2\,$![]() km and $\lambda =5\,$
km and $\lambda =5\,$![]() km (a) and $\lambda =2\,$
km (a) and $\lambda =2\,$![]() km (b) 3262 years after initialization. Red indicates areas where θ is exactly zero. The black line represents the ice extent modelled with Elmer/Ice.
km (b) 3262 years after initialization. Red indicates areas where θ is exactly zero. The black line represents the ice extent modelled with Elmer/Ice.
4. Discussion
4.1. Using the default ice flux limiter
Comparing results obtained with PISM using the default $\lambda =5\,$![]() km with the reference Elmer/Ice simulation reveals comparable sliding speeds (correlation of r = 0.79, Figs 5, 6), but a significant underestimation of shearing speeds and a major ice thickness overestimation in the results obtained with PISM (Figs 3, 7). We attribute the few discrepancies in sliding speeds between Elmer/Ice and PISM with $\lambda =5\,$
km with the reference Elmer/Ice simulation reveals comparable sliding speeds (correlation of r = 0.79, Figs 5, 6), but a significant underestimation of shearing speeds and a major ice thickness overestimation in the results obtained with PISM (Figs 3, 7). We attribute the few discrepancies in sliding speeds between Elmer/Ice and PISM with $\lambda =5\,$![]() km to differences in basal temperatures. The absent diffluence at Sargans in PISM with $\lambda =5\,$
km to differences in basal temperatures. The absent diffluence at Sargans in PISM with $\lambda =5\,$![]() km is caused by the cold-based conditions at the left branch in the PISM with $\lambda =5\,$
km is caused by the cold-based conditions at the left branch in the PISM with $\lambda =5\,$![]() km simulation whereas this area is temperate in Elmer/Ice (Figs 8a, b). The sliding speeds in the main valley are higher than in Elmer/Ice because of the larger extent of temperate-based ice in the PISM with $\lambda =5\,$
km simulation whereas this area is temperate in Elmer/Ice (Figs 8a, b). The sliding speeds in the main valley are higher than in Elmer/Ice because of the larger extent of temperate-based ice in the PISM with $\lambda =5\,$![]() km simulation (Figs 8a, b). Conversely, the poor representation of shearing speeds in PISM with $\lambda =5\,$
km simulation (Figs 8a, b). Conversely, the poor representation of shearing speeds in PISM with $\lambda =5\,$![]() km is caused by the scaling factor θ from the Schoof scheme that is applied to the SIA diffusivity in Eqn (4), with the consequence of decreasing the shearing speed to zero in most of the icefield sector of the Rhine Glacier (Figs 3b, 4a). The reduced ice flux then affects the modelled ice thickness and to a lesser extent also the basal temperatures. Because the modelled sliding speeds of PISM differ from Elmer/Ice only in a small part of the main Rhine Valley, the reduced ice flux due to shearing is compensated for by an increase in the ice thickness of 300–500 m in the icefield sector of the Rhine Glacier (Fig. 7a). As a result of overestimated ice thickness in PISM with $\lambda =5\,$
km is caused by the scaling factor θ from the Schoof scheme that is applied to the SIA diffusivity in Eqn (4), with the consequence of decreasing the shearing speed to zero in most of the icefield sector of the Rhine Glacier (Figs 3b, 4a). The reduced ice flux then affects the modelled ice thickness and to a lesser extent also the basal temperatures. Because the modelled sliding speeds of PISM differ from Elmer/Ice only in a small part of the main Rhine Valley, the reduced ice flux due to shearing is compensated for by an increase in the ice thickness of 300–500 m in the icefield sector of the Rhine Glacier (Fig. 7a). As a result of overestimated ice thickness in PISM with $\lambda =5\,$![]() km, the total ice volume of the Rhine Glacier is also overestimated by 32% (Table 1) despite the fact that the glaciated area is underestimated by 18% at the same time. Furthermore, the overestimated ice thickness in PISM using $\lambda =5\,$
km, the total ice volume of the Rhine Glacier is also overestimated by 32% (Table 1) despite the fact that the glaciated area is underestimated by 18% at the same time. Furthermore, the overestimated ice thickness in PISM using $\lambda =5\,$![]() km better insulates the glacier bed from the cold surface temperatures, leading to 1.5$^\circ$
km better insulates the glacier bed from the cold surface temperatures, leading to 1.5$^\circ$![]() C higher basal temperatures on average than in Elmer/Ice (Fig. 9a). Figure 2 suggests that the Elmer/Ice simulation is very close to an equilibrium state, whereas PISM using $\lambda =5\,$
C higher basal temperatures on average than in Elmer/Ice (Fig. 9a). Figure 2 suggests that the Elmer/Ice simulation is very close to an equilibrium state, whereas PISM using $\lambda =5\,$![]() km shows a significant trend in ice volume, ice area and mean ice thickness growth. Thus the deviations between PISM using $\lambda =5\,$
km shows a significant trend in ice volume, ice area and mean ice thickness growth. Thus the deviations between PISM using $\lambda =5\,$![]() km and Elmer/Ice would be even more substantial if the comparison was done after the year 3262.
km and Elmer/Ice would be even more substantial if the comparison was done after the year 3262.
4.2. Improved agreement by reducing the ice flux limiter
Using PISM with the smallest possible value of $\lambda =1\,$![]() km instead of $\lambda =5\,$
km instead of $\lambda =5\,$![]() km results in a significantly improved agreement with the reference Elmer/Ice simulation in terms of shearing speeds and ice thickness. A smaller value for λ reduces the influence of the Schoof scheme on the shearing speeds. θ is mostly one (i.e. the Schoof scheme does not affect the ice flow) at the Rhine Glacier Piedmont Lobe and a notable portion of the icefield (Fig. 4b), resulting in shearing speeds more similar to those obtained with Elmer/Ice. However, notable deviations from Elmer/Ice shearing speeds remain at some parts of the Rhine Glacier Piedmont Lobe and the main Rhine Valley. PISM shearing speeds become significantly smaller compared with in Elmer/Ice towards the northern and eastern lobe margins while they are similar in the western margin. This pattern correlates with the distribution of cold-based and temperate areas (Fig. 8c). In PISM with $\lambda =1\,$
km results in a significantly improved agreement with the reference Elmer/Ice simulation in terms of shearing speeds and ice thickness. A smaller value for λ reduces the influence of the Schoof scheme on the shearing speeds. θ is mostly one (i.e. the Schoof scheme does not affect the ice flow) at the Rhine Glacier Piedmont Lobe and a notable portion of the icefield (Fig. 4b), resulting in shearing speeds more similar to those obtained with Elmer/Ice. However, notable deviations from Elmer/Ice shearing speeds remain at some parts of the Rhine Glacier Piedmont Lobe and the main Rhine Valley. PISM shearing speeds become significantly smaller compared with in Elmer/Ice towards the northern and eastern lobe margins while they are similar in the western margin. This pattern correlates with the distribution of cold-based and temperate areas (Fig. 8c). In PISM with $\lambda =1\,$![]() km, there are no cold-based areas in the parts of the lobe with small shearing speeds. By contrast, the western part of the lobe is mostly cold-based (Fig. 8c) and shearing speeds are greater, comparable to the Elmer/Ice results. The reason for this correlation between temperate areas and low shearing speeds might be that the continuously temperate bed lowers the basal resistance and as a consequence reduces the surface slope which in turn reduces horizontal shearing. The parameter θ close to one brings about larger shearing speeds in the icefield sector than in PISM with $\lambda =5\,$
km, there are no cold-based areas in the parts of the lobe with small shearing speeds. By contrast, the western part of the lobe is mostly cold-based (Fig. 8c) and shearing speeds are greater, comparable to the Elmer/Ice results. The reason for this correlation between temperate areas and low shearing speeds might be that the continuously temperate bed lowers the basal resistance and as a consequence reduces the surface slope which in turn reduces horizontal shearing. The parameter θ close to one brings about larger shearing speeds in the icefield sector than in PISM with $\lambda =5\,$![]() km. These larger shearing speeds are more similar to Elmer/Ice in terms of pattern and amplitude (Fig. 3). Yet, in the middle of the main Rhine Valley, shearing speeds in PISM with $\lambda =1\,$
km. These larger shearing speeds are more similar to Elmer/Ice in terms of pattern and amplitude (Fig. 3). Yet, in the middle of the main Rhine Valley, shearing speeds in PISM with $\lambda =1\,$![]() km are up to two times larger than in Elmer/Ice. This is in line with findings by Le Meur and others (Reference Le Meur, Gagliardini, Zwinger and Ruokolainen2004) and Adhikari and Marshall (Reference Adhikari and Marshall2013), who have also observed that the shearing speeds in the centre of a valley can be two to three times larger in SIA models than in Stokes models. Although their comparison studies were performed with a setup quite different from the Rhine Glacier during the LGM (temperate valley glaciers with a length of 3–4 km and neglected sliding), the overestimated shearing speeds in valley glaciers occurs for the same reason: lateral and longitudinal stresses that add resistance to the ice flow are neglected in the SIA. Despite the improvements with respect to $\lambda =5\,$
km are up to two times larger than in Elmer/Ice. This is in line with findings by Le Meur and others (Reference Le Meur, Gagliardini, Zwinger and Ruokolainen2004) and Adhikari and Marshall (Reference Adhikari and Marshall2013), who have also observed that the shearing speeds in the centre of a valley can be two to three times larger in SIA models than in Stokes models. Although their comparison studies were performed with a setup quite different from the Rhine Glacier during the LGM (temperate valley glaciers with a length of 3–4 km and neglected sliding), the overestimated shearing speeds in valley glaciers occurs for the same reason: lateral and longitudinal stresses that add resistance to the ice flow are neglected in the SIA. Despite the improvements with respect to $\lambda =5\,$![]() km, θ remains close to or at zero almost everywhere beyond the valley glaciers causing shearing speeds to be much smaller than in Elmer/Ice (Fig. 3c). The improvements in the shearing speeds also affect the modelled ice thickness. Using $\lambda =1\,$
km, θ remains close to or at zero almost everywhere beyond the valley glaciers causing shearing speeds to be much smaller than in Elmer/Ice (Fig. 3c). The improvements in the shearing speeds also affect the modelled ice thickness. Using $\lambda =1\,$![]() km, the modelled ice thickness of PISM deviates by less than $\pm 100\,$
km, the modelled ice thickness of PISM deviates by less than $\pm 100\,$![]() m from Elmer/Ice over most parts of the Rhine Glacier (Fig. 7b). This is significantly better than the 300–500 m of ice thickness overestimation when using $\lambda =5\,$
m from Elmer/Ice over most parts of the Rhine Glacier (Fig. 7b). This is significantly better than the 300–500 m of ice thickness overestimation when using $\lambda =5\,$![]() km and comparable to the uncertainties in trimeline-based ice surface elevation reconstructions in the Alps (Florineth and Schlüchter, Reference Florineth and Schlüchter1998; Florineth, Reference Florineth1998). As a consequence, the overestimation in total ice volume relative to Elmer/Ice is reduced from +32% with $\lambda =5\,$
km and comparable to the uncertainties in trimeline-based ice surface elevation reconstructions in the Alps (Florineth and Schlüchter, Reference Florineth and Schlüchter1998; Florineth, Reference Florineth1998). As a consequence, the overestimation in total ice volume relative to Elmer/Ice is reduced from +32% with $\lambda =5\,$![]() km to only +15% with $\lambda =1\,$
km to only +15% with $\lambda =1\,$![]() km and at the same time matching the ice extent calculated by Elmer/Ice (Table 1). The overestimated ice volume in PISM with $\lambda =1\,$
km and at the same time matching the ice extent calculated by Elmer/Ice (Table 1). The overestimated ice volume in PISM with $\lambda =1\,$![]() km is mostly due to the lobe being 100–200 m thicker than given by Elmer/Ice. In contrast to Elmer/Ice, PISM using $\lambda =1\,$
km is mostly due to the lobe being 100–200 m thicker than given by Elmer/Ice. In contrast to Elmer/Ice, PISM using $\lambda =1\,$![]() km shows a small growing trend in ice volume, ice area and mean ice thickness growth (Fig. 2). Thus the deviations between PISM using $\lambda =1\,$
km shows a small growing trend in ice volume, ice area and mean ice thickness growth (Fig. 2). Thus the deviations between PISM using $\lambda =1\,$![]() km and Elmer/Ice would likely become larger if a comparison was done after the year 3262.
km and Elmer/Ice would likely become larger if a comparison was done after the year 3262.
4.3. Suitability of hybrid dynamics to model icefields
Our model results highlight the fact that the sliding speeds obtained by applying the PISM hybrid model agree reasonably with Elmer/Ice Stokes model. This supports the use of the SSA to compute sliding speeds as implemented in PISM. By contrast, calculating shearing speeds with the SIA is not always appropriate for an icefield like the Rhine Glacier. In the mountainous terrain above the Alpine valleys, the Schoof scheme scales the shearing speeds to zero and thus it is not clear from our comparison study how the SIA alone would perform in these areas. Nonetheless, Le Meur and others (Reference Le Meur, Gagliardini, Zwinger and Ruokolainen2004) found a strong correlation between steep bedrock gradients and increasingly overestimated SIA shearing speeds, which suggests that the hybrid model would likely fail as well to represent the ice dynamics in the steep part of the Rhine Glacier like the mountains flanking the valley glaciers. By contrast, the SIA model performs reasonably well in the open plain where the Piedmont Lobe is situated (Fig. 3c). Despite the shortcomings of the SIA, the hybrid model with a flux limiter is capable of reproducing the Stokes ice thickness in the Alpine valleys within $\pm\!100\,$![]() m and matches the modelled extent of the Stokes model. The mean ice thickness is only 13% greater than in Elmer/Ice. Thus it is feasible to envisage employing a hybrid model at an icefield like the Rhine Glacier during the LGM, but a detailed interpretation of shearing speeds in the valleys should be undertaken with care.
m and matches the modelled extent of the Stokes model. The mean ice thickness is only 13% greater than in Elmer/Ice. Thus it is feasible to envisage employing a hybrid model at an icefield like the Rhine Glacier during the LGM, but a detailed interpretation of shearing speeds in the valleys should be undertaken with care.
4.4. Influence of the ice flux limiter on the ice thickness
Our comparison study reveals that the capability of PISM to model the Rhine Glacier in agreement with the Elmer/Ice Stokes model depends very much on the choice of the parameter λ in the Schoof scheme. Using the default value of $\lambda =5\,$![]() km, which is the recommended value for ice sheets, drastically reduces the ability of PISM to model shearing speeds and ice thickness in a reasonable way within complex and steep topographies such as the icefield sector of the Rhine Glacier. More fundamentally, shearing speeds exactly equal to zero are clearly not expected in steep valleys and thus indicate that $\lambda =5\,$
km, which is the recommended value for ice sheets, drastically reduces the ability of PISM to model shearing speeds and ice thickness in a reasonable way within complex and steep topographies such as the icefield sector of the Rhine Glacier. More fundamentally, shearing speeds exactly equal to zero are clearly not expected in steep valleys and thus indicate that $\lambda =5\,$![]() km is not a meaningful choice for modelling an icefield like the Rhine Glacier. By reducing the effect of the Schoof scheme (i.e. $\lambda =1\,$
km is not a meaningful choice for modelling an icefield like the Rhine Glacier. By reducing the effect of the Schoof scheme (i.e. $\lambda =1\,$![]() km), shearing speeds can be recovered to some extent, and we obtain an ice thickness comparable to the Elmer/Ice results. The difference between using PISM with $\lambda =5\,$
km), shearing speeds can be recovered to some extent, and we obtain an ice thickness comparable to the Elmer/Ice results. The difference between using PISM with $\lambda =5\,$![]() km and $\lambda =1\,$
km and $\lambda =1\,$![]() km seems to be more significant than between Elmer/Ice and PISM using $\lambda =1\,$
km seems to be more significant than between Elmer/Ice and PISM using $\lambda =1\,$![]() km. This indicates that the choice for λ is a key decision for applications like the Rhine Glacier. However, the degree of ice thickness overestimation caused by the Schoof scheme might also depend on the parametrization of sliding. Indeed, the ice flux arises solely from the SSA (i.e. is governed exclusively by sliding) in areas where the Schoof scheme reduces shearing speeds to zero. Thus a different parametrization of sliding than in this study might well affect the ice thickness overestimation in a different way.
km. This indicates that the choice for λ is a key decision for applications like the Rhine Glacier. However, the degree of ice thickness overestimation caused by the Schoof scheme might also depend on the parametrization of sliding. Indeed, the ice flux arises solely from the SSA (i.e. is governed exclusively by sliding) in areas where the Schoof scheme reduces shearing speeds to zero. Thus a different parametrization of sliding than in this study might well affect the ice thickness overestimation in a different way.
4.5. Interaction between the Schoof scheme and model resolution
When PISM is used with the default value $\lambda =5\,$![]() km, the choice between a horizontal resolution of $1$
km, the choice between a horizontal resolution of $1$![]() or $2 \,$
or $2 \,$![]() km does not seem to have a notable influence on the agreement with Elmer/Ice (Figs 7a, 10a). In both cases, the ice thickness is similarly overestimated, which is caused by the Schoof scheme that reduces shearing speeds to zero at a major part of the Rhine Glacier (Fig. 11a). If PISM is used at horizontal resolutions of $1$
km does not seem to have a notable influence on the agreement with Elmer/Ice (Figs 7a, 10a). In both cases, the ice thickness is similarly overestimated, which is caused by the Schoof scheme that reduces shearing speeds to zero at a major part of the Rhine Glacier (Fig. 11a). If PISM is used at horizontal resolutions of $1$![]() and $2\,$
and $2\,$![]() km with the smallest non-zero value for λ (i.e. $\lambda =1\,$
km with the smallest non-zero value for λ (i.e. $\lambda =1\,$![]() km and $\lambda =2\,$
km and $\lambda =2\,$![]() km), the ice extent is in both cases consistent with Elmer/Ice but small differences in ice thickness overestimation emerge (Figs 7b, 10b). In more detail, the PISM simulation using a resolution of $2\,$
km), the ice extent is in both cases consistent with Elmer/Ice but small differences in ice thickness overestimation emerge (Figs 7b, 10b). In more detail, the PISM simulation using a resolution of $2\,$![]() km and $\lambda =2\,$
km and $\lambda =2\,$![]() km overestimates the mean ice thickness by $88\,$
km overestimates the mean ice thickness by $88\,$![]() m (+21%) whereas the mean overestimation for the simulation using a resolution of $1\,$
m (+21%) whereas the mean overestimation for the simulation using a resolution of $1\,$![]() km and $\lambda =1\,$
km and $\lambda =1\,$![]() km is only $56\,$
km is only $56\,$![]() m (+13%). In more detail, Figures 7b and 10b suggest that the ice excess in the $2\,$
m (+13%). In more detail, Figures 7b and 10b suggest that the ice excess in the $2\,$![]() km simulation is located predominantly in the icefield sector instead of at the Rhine Glacier Piedmont Lobe as it was the case in the $1\,$
km simulation is located predominantly in the icefield sector instead of at the Rhine Glacier Piedmont Lobe as it was the case in the $1\,$![]() km simulation. We attribute this to the θ values in the main Rhine Valley which are smaller in the $2\,$
km simulation. We attribute this to the θ values in the main Rhine Valley which are smaller in the $2\,$![]() km simulation than in the $1\,$
km simulation than in the $1\,$![]() km simulation (Figs 4b, 11b). Thus, reducing λ to its minimum value results in a significantly improved agreement with Elmer/Ice at horizontal resolutions of both $1$
km simulation (Figs 4b, 11b). Thus, reducing λ to its minimum value results in a significantly improved agreement with Elmer/Ice at horizontal resolutions of both $1$![]() and $2\,$
and $2\,$![]() km. Yet, the PISM results using a resolution of $2\,$
km. Yet, the PISM results using a resolution of $2\,$![]() km differ a bit more from the ones of Elmer/Ice. This is likely not only due to the Schoof scheme which yields slightly smaller θ values but also because a horizontal resolution of $2\,$
km differ a bit more from the ones of Elmer/Ice. This is likely not only due to the Schoof scheme which yields slightly smaller θ values but also because a horizontal resolution of $2\,$![]() km does not resolve the topography as well at a resolution of $1\,$
km does not resolve the topography as well at a resolution of $1\,$![]() km.
km.
4.6. Computational speed of PISM
It must be stressed that achieving the improvements in shearing speeds and ice thickness of PISM by reducing λ from 5 to 1 km causes the computational time to roughly double. PISM integrates the ice dynamics explicitly with the forward-time central-space scheme using adaptive time stepping (Bueler and Brown, Reference Bueler and Brown2009). PISM takes the largest possible time step that maintains numerical stability in the SIA, the SSA and the enthalpy model. In our model setup it is almost always the SIA that requires the shortest time step. The largest possible time step for the SIA is proportional to the inverse of the highest SIA diffusivity (Eqn (4)) on the model domain (Hindmarsh, Reference Hindmarsh2001), which is controlled by the Schoof scheme in our case. Indeed, smaller λ values (e.g. 1 km) allow for higher diffusivities, but then require shorter time steps, and therefore increase the computational time. Thus, there is a trade-off between improved computational efficiency and misrepresented shearing speeds and ice thicknesses when using the Schoof scheme to reduce computational time. The higher computational costs are a drawback for applying the $\lambda =1\,$![]() km setup of PISM on longer periods like the last glacial cycle (120 000 years), or over the entire Alps (15 times larger area than the Rhine Glacier) (Seguinot and others, Reference Seguinot2018).
km setup of PISM on longer periods like the last glacial cycle (120 000 years), or over the entire Alps (15 times larger area than the Rhine Glacier) (Seguinot and others, Reference Seguinot2018).
4.7. Implications for previous PISM applications in the European Alps
The significantly increased ice thickness resulting from the default setting in the Schoof scheme in PISM ($\lambda =5\,$![]() km) raises the question whether it can explain the systematic overestimation found in previous PISM-based paleo modelling of the AlpIF (Becker and others, Reference Becker, Seguinot, Jouvet and Funk2016, Reference Becker, Funk, Schlüchter and Hutter2017; Seguinot and others, Reference Seguinot2018). Among these studies, it is only Seguinot and others (Reference Seguinot2018) who state the value of λ they used. In their study, PISM was run with $\lambda =5\,$
km) raises the question whether it can explain the systematic overestimation found in previous PISM-based paleo modelling of the AlpIF (Becker and others, Reference Becker, Seguinot, Jouvet and Funk2016, Reference Becker, Funk, Schlüchter and Hutter2017; Seguinot and others, Reference Seguinot2018). Among these studies, it is only Seguinot and others (Reference Seguinot2018) who state the value of λ they used. In their study, PISM was run with $\lambda =5\,$![]() km. Unfortunately, they do not give ice thickness deviations for the Rhine Glacier but for a larger neighbouring glacier, the Rhone Glacier. For this glacier, they found ice thickness overestimations averaging to 861 m (Seguinot and others, Reference Seguinot2018) in the valley part, which is 1.5–3 times greater than what we have found for the valley part of the Rhine Glacier. Nevertheless, a direct extrapolation of the ice thickness overestimation from the Rhine Glacier to the Rhone Glacier is difficult because the latter is considerably larger and includes significantly higher mountain peaks upon which the Schoof scheme might react differently. Apart from this, the earlier ice thickness overestimations are referenced to the geomorphologically reconstructed ice thicknesses and not a Stokes reference simulation like in this study. Further, Seguinot and others (Reference Seguinot2018) used different sliding and mass-balance parametrizations than this study. Thus a closer investigation is necessary to pin down in detail to what percentage the former ice thickness overestimations were caused by the Schoof scheme. But since Seguinot and others (Reference Seguinot2018) used $\lambda =5\,$
km. Unfortunately, they do not give ice thickness deviations for the Rhine Glacier but for a larger neighbouring glacier, the Rhone Glacier. For this glacier, they found ice thickness overestimations averaging to 861 m (Seguinot and others, Reference Seguinot2018) in the valley part, which is 1.5–3 times greater than what we have found for the valley part of the Rhine Glacier. Nevertheless, a direct extrapolation of the ice thickness overestimation from the Rhine Glacier to the Rhone Glacier is difficult because the latter is considerably larger and includes significantly higher mountain peaks upon which the Schoof scheme might react differently. Apart from this, the earlier ice thickness overestimations are referenced to the geomorphologically reconstructed ice thicknesses and not a Stokes reference simulation like in this study. Further, Seguinot and others (Reference Seguinot2018) used different sliding and mass-balance parametrizations than this study. Thus a closer investigation is necessary to pin down in detail to what percentage the former ice thickness overestimations were caused by the Schoof scheme. But since Seguinot and others (Reference Seguinot2018) used $\lambda =5\,$![]() km, it seems likely that at least a part of their ice thickness overestimation was caused by their choice of λ.
km, it seems likely that at least a part of their ice thickness overestimation was caused by their choice of λ.
5. Conclusions
We performed four simulations of the Rhine Glacier during the LGM using the hybrid model PISM. Two simulations used a horizontal resolution of $1\,$![]() km and two used $2\,$
km and two used $2\,$![]() km. For each PISM resolution pair, we tested two degrees of flux limitation for the SIA: the default $\lambda =5$
km. For each PISM resolution pair, we tested two degrees of flux limitation for the SIA: the default $\lambda =5$![]() km and the smallest possible value for λ which is equal to the model resolution. The model setup was very similar to the one employed earlier by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) who used the Stokes model Elmer/Ice instead. We compared the PISM simulations to the reference Elmer/Ice simulation in terms of modelled ice speeds, ice thickness and basal temperatures in order to assess the ability of hybrid models to simulate icefields and piedmont lobes. Based on this comparison we draw the following conclusions:
km and the smallest possible value for λ which is equal to the model resolution. The model setup was very similar to the one employed earlier by Cohen and others (Reference Cohen, Gillet-Chaulet, Haeberli, Machguth and Fischer2018) who used the Stokes model Elmer/Ice instead. We compared the PISM simulations to the reference Elmer/Ice simulation in terms of modelled ice speeds, ice thickness and basal temperatures in order to assess the ability of hybrid models to simulate icefields and piedmont lobes. Based on this comparison we draw the following conclusions:
(1) Using the default degree of ice flux limitation for PISM causes a strong underestimation of shearing speeds. As a consequence, the ice thickness in the icefield sector is overestimated by 300–500 m compared to Elmer/Ice. This mechanism has the potential to explain a sizeable part of the ice thickness overestimations found by earlier studies employing PISM in the European Alps. Nonetheless, a specialized study is necessary to illuminate this in detail because this study differs from earlier studies in the sliding and mass-balance parametrizations as well as the reference ice thickness.
(2) Using the weaker flux limiter, the hybrid SIA/SSA ice flow dynamics captures the large-scale dynamics at our icefield in good agreement with the Stokes ice dynamics. Sliding speeds and basal temperatures show a good agreement between the two models. Although SIA shearing speeds remain overestimated in the main valleys, the hybrid scheme reproduces the Stokes ice thickness and extent well. However, the improved setup comes with increased computational costs.
There are some limitations of our study that are important to keep in mind. Our assessment of the hybrid scheme is specific to our choice for ice flow parameters as well as the parametrization of sliding. Further, the Schoof scheme might affect the modelled ice thickness and shearing speeds more strongly at smaller stages of the Rhine Glacier or for glaciers located in more complex and steeper terrain. Using a different parametrizations of sliding might impact how the Schoof scheme affects modelled shearing speeds and ice thickness. For future studies involving applications similar to the one presented here, we strongly recommend evaluating the influence of the Schoof scheme on the PISM results and choose an appropriate λ. In our case, the best model results were achieved using λ equal to the model resolution.
Data
Data is available on request.
Acknowledgments
MI is supported by the Swiss National Science Foundation (SNSF), project 200021-162444. JS was supported by SNSF project 200020-169558 and 200021-153179/1 to MF. MI is grateful to Kolumban Hutter for the interesting discussions, to Everarda van Dongen for the feedback on visualizations, and to Simon Förster for the support in Python and C++. Development of PISM is supported by NASA grant NNX17AG65G and NSF grants PLR-1603799 and PLR-1644277. We thank Tong Zhang and the anonymous referee for their comments which contributed to improve the manuscript.
Author contributions
The study was designed by MI, GJ, DC and MF. MI performed the PISM simulations, analysed the output and wrote the manuscript closely advised by GJ and with the support of all co-authors. AA, DC, MF and JS provided valuable input to the discussion.
Conflict of interest
The authors declare that they have no conflict of interest.















