A mass-flux perspective of the tidewater glacier cycle

Abstract

I explore the tidewater glacier cycle with a 1-D, depth- and width-integrated flow model that includes a mass-flux calving parameterization. The parameterization is developed from mass continuity arguments and relates the calving rate to the terminus velocity and the terminus balance velocity. The model demonstrates variable sensitivity to climate. From an advanced, stable configuration, a small warming of the climate triggers a rapid retreat that causes large-scale drawdown and is enhanced by positive glacier-dynamic feedbacks. Eventually, the terminus retreats out of deep water and the terminus velocity decreases, resulting in reduced drawdown and the potential for restabilization. Terminus readvance can be initiated by cooling the climate. Terminus advance into deep water is difficult to sustain, however, due to negative feedbacks between glacier dynamics and surface mass balance. Despite uncertainty in the precise form of the parameterization, the model provides a simple explanation of the tidewater glacier cycle and can be used to evaluate the response of tidewater glaciers to climate variability. It also highlights the importance of improving parameterizations of calving rates and of incorporating sediment dynamics into tidewater glacier models.

1. INTRODUCTION

Tidewater glaciers, i.e. those that terminate in the ocean, respond nonlinearly to climate and ocean variability due to complex relationships between glacier geometry and ice flow (Post and others, 2011). The complexity of these relationships is illustrated in regional studies of tidewater glaciers in Alaska (McNabb and Hock, 2014) and Greenland (Moon and Joughin, 2008), which document asynchronous fluctuations in terminus position of adjacent glaciers that are subjected to similar forcings. Efforts to improve understanding of tidewater glaciers are motivated by the significant impacts of tidewater glacier behavior on sea level rise (e.g., Pfeffer and others, 2008) and proglacial environments (O'Neel and others, 2015). A classic example of the magnitude of these impacts is provided by the disintegration of the Glacier Bay Icefield, Alaska. The icefield has retreated over 100 km since 1770, lost more than 3000 km³ of ice, contributed about 8 mm to global sea level rise (Larsen and others, 2005) and opened up a bay that is now a rich marine habitat.

The response of tidewater glaciers to climate and ocean variability is poorly constrained due to deficiences in our understanding of iceberg calving and submarine melting. Previous work has related iceberg calving to water depth at the terminus (e.g. Brown and others, 1982; Pelto and Warren, 1991), terminus height and terminus height above buoyancy (van der Veen, 1996, 2002; Vieli and others, 2000, 2001; Bassis and Walker, 2012), and near-terminus strain rates (Benn and others, 2007a, b; Alley and others, 2008; Amundson and Truffer, 2010; Nick and others, 2010; Levermann and others, 2012), while submarine melting has been linked to subglacial discharge and fjord temperature (e.g. Jenkins, 2011; Xu and others, 2012; Motyka and others, 2013). There remains much uncertainty regarding the physics of the glacier–ocean interface despite the important insights provided by these previous studies. The issue is exacerbated by difficulties associated with reconciling the short time- and length-scale processes that contribute to calving and submarine melting with the computational constraints of long time- and length-scale flow models. Consequently, confidence in prognostic tidewater glacier models is low.

In this paper, I adopt an alternative approach to modeling the evolution of tidewater glaciers that is inspired by the ‘tidewater glacier cycle’ (Post, 1975). Observations from Alaska indicate that tidewater glaciers can undergo cycles of rapid retreat and slow readvance even during periods of relatively stable climate. Starting from an advanced, steady-state configuration (Fig. 1a), a small increase in the equilibrium line altitude (ELA) can cause the terminus to retreat into an overdeepening or through a constriction. This initiates a runaway process (Fig. 1b) in which a loss of basal and/or lateral resistance causes flow acceleration, dynamic thinning, enhanced calving activity and further loss of resistance (Meier and Post, 1987; Pfeffer, 2007), resulting in tens of kilometers of retreat over several decades (e.g. Larsen and others, 2005; McNabb and Hock, 2014). Retreat stops when the terminus reaches a shallow and/or narrow pinning point or retreats out of the water (Fig. 1c). Subsequent terminus readvance can occur either by decreasing the ELA and/or building a moraine at the terminus that limits calving and submarine melting (Meier and Post, 1987; Post and Motyka, 1995) (Fig. 1d). It takes tidewater glaciers hundreds of years to advance down fjord.

Fig. 1. Schematic of the tidewater glacier cycle. (a) Advanced, stable configuration with high climate sensitivity. A small rise in the ELA can trigger a rapid retreat. (b) Rapid terminus retreat driven by glacier dynamics. Climate sensitivity is very low. (c) Retreated, stable configuration. A decrease in the ELA, or increase in resistance to flow, can enable the glacier to thicken and begin advancing. Climate sensitivity is moderate. (d) Slow advance enabled by increased resistance from a push moraine. A rise in the ELA can trigger a calving retreat prior to the terminus reaching the end of the fjord.

Here, I propose a heuristic calving parameterization that is consistent with the tidewater glacier cycle, has few parameters and works for both grounded and floating termini. I start by using mass-flux arguments to develop the parameterization, which I then apply to a one-dimensional (1-D), depth- and width-integrated flow model. The parameterization and model provide insights into tidewater glacier dynamics, surface mass balance feedbacks and the behavior of previously proposed calving parameterizations.

2. MASS-FLUX CALVING PARAMETERIZATION

At its simplest, the tidewater glacier cycle can be described in terms of three basic parameters: the terminus balance velocity (net surface and basal mass balance divided by the cross-sectional area of the terminus; hereafter referred to as the ‘balance velocity’), U _b, the mean terminus velocity, U _t, and the mean frontal ablation rate, U _f, which includes iceberg calving and submarine melting. When a tidewater glacier is in steady-state, the balance velocity, terminus velocity and frontal ablation rate must be equal (U _b = U _t = U _f). During retreat the terminus velocity tends to exceed the balance velocity, which leads to thinning (U _f > U _t > U _b), whereas during advance the balance velocity tends to exceed the terminus velocity, which leads to thickening (U _b > U _t > U _f). Here, I develop a mass-flux calving parameterization that satisfies these conditions and is consistent with available data.

Since I will later explore the tidewater glacier cycle with a 1-D, depth- and width-integrated flow model, I develop the parameterization using the corresponding mass continuity equation (van der Veen, 2013) in which

(1) $$\displaystyle{{\partial H} \over {\partial t}} = \dot B - \displaystyle{1 \over W}\displaystyle{\partial \over {\partial x}}(UHW),$$

where U is the depth- and width-averaged velocity, H and W are the glacier thickness and width, and $\dot B$ is the specific (surface plus basal) mass balance rate (m ice eq.). Integrating over the length of the glacier L, applying the Leibniz integral rule, and dividing by the terminus height H _t, yields

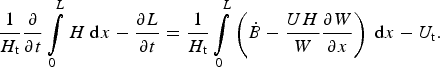(2) $$\displaystyle{1 \over {{H_{\rm t}}}}\displaystyle{\partial \over {\partial t}}\int\limits_0^L {H\;{\rm d}x - \displaystyle{{\partial L} \over {\partial t}} = \displaystyle{1 \over {{H_{\rm t}}}}} \int\limits_0^L {\left( {\dot B - \displaystyle{{UH} \over W}\displaystyle{{\partial W} \over {\partial x}}} \right)\;{\rm d}x - {U_{\rm t}}}. $$

Equation (2) can be simplified by noting that the glacier-wide balance velocity is given by

(3) $${U_{\rm b}} = \displaystyle{1 \over {{H_{\rm t}}}}\int\limits_0^L {\left( {\dot B - \displaystyle{{UH} \over W}\displaystyle{{\partial W} \over {\partial x}}} \right)\;{\rm d}x} $$

and that the longitudinal cross-sectional area, A _L , is

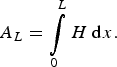(4) $${A_L} = \int\limits_0^L {H\;{\rm d}x}. $$

Substituting Eqns (3) and (4) into (2) and solving for the rate of length change gives

(5) $$\displaystyle{{\partial L} \over {\partial t}} = \displaystyle{1 \over {{H_t}}}\displaystyle{{\partial {A_L}} \over {\partial t}} + {U_{\rm t}} - {U_{\rm b}}.$$

The rate of change of longitudinal area cannot be solved directly. However, as described above, for tidewater glaciers terminus retreat is associated with surface lowering and flow acceleration while terminus advance is associated with thickening and (relatively) slow glacier flow. This suggests that, to first-order,

(6) $$\displaystyle{1 \over {{H_{\rm t}}}}\displaystyle{{\partial {A_L}} \over {\partial t}} \approx \alpha ({U_{\rm b}} - {U_{\rm t}}),$$

where α > 1 is a dimensionless calving factor. In other words, the glacier will tend to grow in volume when the balance velocity exceeds the terminus velocity. Inserting Eqn (6) into (5) yields

(7) $$\displaystyle{{\partial L} \over {\partial t}} = (\alpha - 1)({U_{\rm b}} - {U_{\rm t}}).$$

When a glacier is in steady-state (1) the volume is constant, implying that the balance velocity equals the frontal ablation rate, and (2) the length is constant, implying that the terminus velocity also equals the frontal ablation rate. Equations (6) and (7) are consistent with these steady-state conditions.

Although Eqn (7) is sufficient for implementation in a flow model, it is instructive to write it in terms of the calving rate, U _c. The rate of length change can then be expressed as

(8) $$\displaystyle{{\partial L} \over {\partial t}} = {U_{\rm t}} - {U_{\rm c}} - \dot m,$$

where $\dot m$ is the depth- and width-averaged submarine melt rate along the vertical face of the terminus. Equating Eqns (7) and (8) and rearranging yields

(9) $${U_{\rm c}} = \alpha {U_{\rm t}} + (1 - \alpha ){U_{\rm b}} - \dot m,$$

which can easily be expressed in terms of fluxes by multiplying both sides of the equation by the cross-sectional area of the terminus. I will therefore refer to Eqn (9) as a mass-flux calving parameterization and will discuss it in terms of both rates and fluxes.

Equation (9) highlights the intricate ways in which submarine melting can affect calving. First, net melting of the vertical face of the terminus, $\dot m$ , can act to reduce the calving rate because submarine melting removes ice before it is able to calve off of the glacier. In this respect, it does not matter whether U _c and $\dot m$ are treated separately or as a combined frontal ablation rate. On the other hand, non-uniform melting of the vertical face of the terminus may influence calving by changing the near-terminus stress field and promoting longitudinal extension and fracture growth (e.g. O'Leary and Christofferson, 2013); this effect could be accounted for by making the calving factor dependent on submarine melting. Finally, basal melting of an ice shelf affects both (1) the supply of ice to the terminus (i.e. the balance velocity) and (2) ice velocities and strain rates by affecting the total drag along the margins of the ice shelf. To simplify the following modeling analysis and discussion, I will hereafter set $\dot m = 0$ , with the additional expectation that variations in submarine melting are relatively small compared with variations in calving over the long timescales of the tidewater glacier cycle. Thus,

(10) $${U_{\rm c}} = \alpha {U_{\rm t}} + (1 - \alpha ){U_{\rm b}},$$

or equivalently,

(11) $$({U_{\rm c}} - {U_{\rm b}}) = \alpha ({U_{\rm t}} - {U_{\rm b}}).$$

In addition to being broadly consistent with the tidewater glacier cycle, the mass-flux calving parameterization is also consistent with recent observations of tidewater glaciers. For example, Howat and others (2011) report monthly mass balance fluxes, ice fluxes at transects upstream from glacier termini, and rates of terminus volume change for Helheim Glacier, Kangerlussuaq Glacier and Jakobshavn Isbræ for the period 2000–10. I apply a 12 month running average to their data and calculate calving fluxes by using mass continuity and assuming that mass losses from the terminus region (lowermost 10 km of the glaciers) are predominately due to calving. Thus, I assume that

(12) $${Q_{\rm c}} = {Q_{in}} - \displaystyle{{{\rm d}V} \over {{\rm d}t}},$$

where Q _in is the ice flux into the terminus area and V is the volume of the terminus downstream from the ice flux transect. Furthermore, I also assume that ice fluxes upstream from the termini are representative of terminus ice fluxes (i.e. Q _t ≈ Q _in ). Under these assumptions, Howat and other's (2011) data show a strong linear correlation between Q _c − Q _b and Q _t − Q _b (Eqn (11)), with a best fit slope of α = 1.14 and slope uncertainty of 0.03 (Fig. 2a). This correlation is slightly higher than the correlation between Q _c and Q _t (Fig. 2b) and appears to have more randomly distributed residuals. The high correlation is not surprising since (1) the calving flux is calculated from the ice flux (Eqn (12)) and (2) previous work has demonstrated that ice fluxes and calving fluxes are nearly linearly related over annual and longer time scales (van der Veen, 1996, 2002), suggesting that calving fluxes and ice fluxes are not independent (Amundson and Truffer, 2010).

Fig. 2. Mass fluxes at Helheim Glacier, Kangerlussuaq Glacier and Jakobshavn Isbræ, Greenland, from 2000 to 2010. Data from Howat and others (2011). (a) Calving flux minus balance flux versus ice flux minus balance flux. (b) Calving flux (includes submarine melting) versus ice flux. In both panels, α indicates the best-fit slope of a linear regression; in (a), it specifically corresponds to the calving factor in the mass-flux calving parameterization (Eqn (11)).

The mass-flux calving parameterization essentially represents a small, but important, modification to the previously observed proportionality between calving and ice flow. If calving was truly proportional to ice flow, then tidewater glaciers would either always retreat or always advance. The (1 − α)U _b term in Eqn (10) can therefore be thought of as a small correction that provides a mechanism for the calving rate to be either larger or smaller than the ice velocity. Furthermore, because α appears to be close to 1, variations in the calving rate are more strongly influenced by variations in terminus velocity than by variations in balance velocity.

There are a few caveats with the calving parameterization. First, steady-state can be achieved during model spin-up at any number of fixed terminus locations. Thus, in prognostic models it may be necessary to spin-up the model through several climate cycles to identify locations where the terminus will naturally stabilize. Second, in the parameterization the calving rate responds instantaneously to changes in surface and basal mass balance, even if those changes occur far upglacier from the terminus. In this sense, the parameterization requires that changes in surface and basal mass balance are slow and uniformly distributed across the glacier. However, given that the parameterization places more weight on changes in terminus velocity, non-uniform changes in surface and basal mass balance will likely have a small effect on model output. Finally, the parameterization treats variations in terminus position as a continuous process. Consequently, the parameterization is unable to account for some potentially important processes, such as nonlinear glacier response to variable size and frequency of calving events (Amundson and Truffer, 2010; Bassis, 2011). The calving factor α is likely to depend on these, and other, complex processes. In the model experiments below, I will treat the calving factor as a constant and test the model sensitivity to the choice of this constant.

A more thorough analysis of the mass-flux calving parameterization would require data on terminus velocities, calving rates and balance velocities that span the duration of a complete tidewater glacier cycle. Unfortunately, however, these data do not currently exist. Nonetheless, despite uncertainty in the form of the parameterization, it appears to be consistent with available data and provides a starting point for discussing tidewater glacier dynamics in terms of mass fluxes.

3. NUMERICAL MODEL

I apply the mass-flux calving parameterization to a 1-D, depth- and width-integrated flow model. The model formulation works well for fast glacier flow in relatively narrow, well defined channels and has been used in the past to investigate glacier sensitivity to external forcings (Nick and others, 2009, 2010, 2012; Vieli and Nick, 2011), geometry (Enderlin and others, 2013a) and parameter uncertainty (Enderlin and others, 2013b). My aim with these experiments is to explore the general, large-scale behavior of tidewater glaciers. I therefore choose to use an ad hoc glacier geometry (Fig. 3) that is based on commonly observed geometries of glaciers and fjords in Alaska (e.g. Nolan and others, 1995; Nick and others, 2007; Motyka and others, 2013). The model domain consists of a large accumulation area that funnels ice into a fjord that reaches depths of a few hundred meters and has two shallow sills. The cross-sectional geometry is assumed to be rectangular, so that glacier width does not vary with time.

Fig. 3. Model domain used for numerical experiments. (a) Bedrock topography and (b) map view geometry.

3.1. Model equations

For a 1-D depth- and width-integrated flow model (van der Veen, 2013), conservation of momentum requires that

(13) $$\eqalign{2\displaystyle{\partial \over {\partial x}}\left( {H\nu \displaystyle{{\partial U} \over {\partial x}}} \right) & - \beta N{\left \vert U \right \vert ^{(1 - p)/p}}\cr & \quad U - \displaystyle{{2H} \over W}{\left( {\displaystyle{5 \over {AW}}} \right)^{1/3}}{\left \vert U \right \vert ^{ - 2/3}}U = {\rho _i}gH\displaystyle{{\partial h} \over {\partial x}},} $$

where β is the basal roughness factor, N is the effective basal pressure, p is the sliding law exponent, A is the flow rate factor, ρ _i  = 917 kg m⁻³ is ice density, h is the glacier surface elevation and ν is the depth-averaged effective viscosity, defined as

(14) $$\nu = {A^{ - 1/3}}{\left \vert {\displaystyle{{\partial U} \over {\partial x}}} \right \vert ^{ - 2/3}}.$$

Equation (13) states that the driving stress is balanced by basal drag, lateral drag and gradients in longitudinal stress.

The basal drag is assumed to depend on basal roughness, effective pressure and sliding velocity. Values for the sliding law exponent reported in the literature range from 1 to 3. According to Enderlin and others (2013b), the choice of p does not have a significant impact on the steady-state solutions for tidewater glaciers but it does impact the timescale of glacier response to a perturbation, with lower values of p causing a more rapid response. I arbitrarily choose to use an intermediate value of p = 2. I also use a constant basal roughness factor, β = 22 s^1/2 m^−1/2, which translates to a low maximum basal resistance, βNU ^1/p , of $\sim {10^8}\;{\rm Pa}\,{\rm s}\,{{\rm m}^{ - 1}}$ (MacAyeal and others, 1995). The effective pressure is calculated by defining a linear phreatic surface that starts at the glacier bed at the divide and decreases to sea level at the glacier terminus. The minimum permitted effective pressure is 0, which occurs when the glacier develops a floating ice shelf.

Both the effective viscosity and the lateral drag depend on the flow rate factor. I use a constant flow rate factor and assume that the ice is temperate (consistent with tidewater glaciers in Alaska and other low-latitude regions) so that A = 2.4 × 10⁻²⁴ Pa⁻³ s⁻¹ (Cuffey and Paterson, 2010).

After solving the momentum balance equation using the appropriate boundary conditions (see below), the glacier geometry is evolved by applying the calculated velocities to the mass continuity equation (Eqn (1)) and the parameterized rate of length change (Eqn (7)). The mass balance, which is required for both Eqns (1) and (7), is prescribed using a constant mass balance gradient and enforcing a maximum accumulation rate, such that

(15) $$\dot B(z) = \min (\Gamma (z - {z_{{\rm ELA}}}),\;\max \dot B),$$

where Γ is the mass balance gradient, z is elevation and z _ELA is the elevation of the ELA. I set Γ = −10/1300 a⁻¹ and $\max \dot B = 4\,{\rm m}\,{{\rm a}^{ - 1}}$ to roughly mimic the climate of maritime glaciers in Alaska (Van Beusekom and others, 2010).

A Dirichlet boundary condition is used to prescribe a velocity of U = 0 at the divide (x = 0), and a Neumann boundary condition to prescribe the velocity gradient at the terminus (Eqn (17) below). The depth-integrated, longitudinal deviatoric stress, σ′ _xx , at the terminus is found by subtracting the depth-integrated hydrostatic pressure from the depth-integrated glaciostatic pressure, giving

(16) $${\sigma ^{\prime}_{xx}}{ {(x = L)}} = \displaystyle{1 \over 2}{\rho _i}g\left( {H - \displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}\displaystyle{{{D^2}} \over H}} \right),$$

where ρ _w = 1028 kg m⁻³ is the density of sea water and D is the submerged depth of the terminus. Inserting Eqn (16) into Glen's Flow Law gives

(17) $$\displaystyle{{\partial U} \over {\partial x}}{ {(x = L)}} = A{\left[ {\displaystyle{{{\rho _i}g} \over 4}\left( {H - \displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}\displaystyle{{{D^2}} \over H}} \right)} \right]^3}.$$

The model equations are solved using a moving grid that tracks the grounding line (for stability; Vieli and Payne, 2005) with a small grid spacing (Δx = 100 m) and small time steps (Δt = 0.01 a). The location of the terminus is tracked separately. Details of the numerical method are presented by Enderlin and others (2013a).

3.2. Model experiments

I performed a series of experiments to explore the large-scale behavior of tidewater glacier advance and retreat. The model was initialized with a fixed length of L = 127.5 km (the terminus was positioned on top of the shallow sill at the end of the model domain) and an ELA of 1300 m, and was run until it reached steady-state, defined as occurring when |dL/dt| <1 m a⁻¹. From this advanced, stable configuration, terminus retreat was initiated by raising the ELA at a constant rate of 5 m a⁻¹ for 10–40 years until reaching new ELAs of 1350, 1400, 1450 and 1500 m. This was repeated for several different calving factors, ranging from α = 1.1 to α = 1.3. The model runs were terminated when the glacier reached a new steady-state.

Terminus readvance was simulated by starting with the final state from each of the retreat simulations, and then lowering the ELA back to the original ELA of 1300 m. The impact of restraining forces from a proglacial moraine during advance was also investigated by incorporating an additional back stress on the terminus. The additional back stress linearly increased from 0 to 8 × 10⁵ Pa (corresponding to a moraine that is a few tens of meters tall; Fischer and Powell, 1998) over the first 80 years, and was subsequently held constant. This approach was chosen over implementing a sediment model (e.g. Oerlemans and Nick, 2006; Nick and others, 2007) because sediment dynamics, which are poorly constrained, are beyond the scope of this paper and because this approach more clearly relates the resistance at the terminus to glacier thickening and terminus advance.

4. MODEL RESULTS AND INTERPRETATION

4.1. Terminus retreat

When applied to a 1-D flow model, the mass-flux calving parameterization was capable of producing tens of kilometers of retreat over 100–200 years (Fig. 4). Retreat from an extended, steady-state configuration was initiated by quickly raising the ELA and then holding it steady. The initial stages of retreat were slow because (1) variations in calving were dominated by variations in terminus velocity (Eqn (10)) and (2) terminus velocity did not undergo significant changes until the terminus started to retreat into deep water. For example, for the model results shown in Figure 4b, the ELA rose from 1300 to 1400 m in the first 20 years of the simulation; during that time the balance velocity decreased from 830 to 480 m a⁻¹ but the terminus retreated only 880 m. Once the terminus retreated into deep water, however, the rate of retreat abruptly increased and was governed by glacier-dynamic feedbacks that resulted in the terminus velocity and calving rate increasing by more than a factor of 4. As the terminus retreated out of deep water the velocity gradually decreased until it equaled the balance velocity, at which point the glacier reached a new steady-state. During retreat, the terminus was unstable when retreating down a reverse bed and stabilized on a seaward sloping bed.

Fig. 4. Modeled terminus retreat for three different combinations of final ELA and calving factor. The first two rows show the calving rate, terminus velocity, balance velocity and resultant rate of length change. The next two rows show the calving flux, terminus flux, balance flux and resultant rate of volume change. The bottom row indicates the initial and final steady-state geometries (indicated by dashed and solid curves, respectively).

Interestingly, the terminus always went afloat as it was retreating upslope (Fig. 5); similar behavior has been observed at Columbia Glacier during its ongoing retreat (Walter and others, 2010). This likely occurs because ice flow over bedrock topography produces spatial variations in strain rates (e.g. Gudmundsson, 2003; Raymond and Gudmundsson, 2005; Sergienko and others, 2007). Enhanced stretching occurs when the ice near the terminus passes over a shallow sill, which allows the terminus to thin to flotation more quickly than it can retreat. Formation of a floating ice shelf gives the ocean access to the base of the glacier, which further destabilizes the terminus through basal melting (Motyka and others, 2011); this positive feedback was not accounted for in the model.

Fig. 5. Formation of floating ice shelves during retreat for different combinations of final ELA and α. (a) Terminus height above flotation versus Glacier-length for each of the three model runs shown in Figure 4 (the plots lie on top of each other), plotted over an image of the model domain. (b) Height above flotation versus bed slope at the terminus/grounding line, where h _b is the bed elevation. Color indicates model year. Note that the terminus is often at flotation when ∂h _b/∂x < 0.

The model demonstrated that, once a retreat has been initiated, the rate of retreat is insensitive to the size of the climate perturbation (Figs 4a and b); this is because during retreat the balance velocity is almost an order of magnitude smaller than either the terminus velocity or calving rate. Furthermore, variations in the balance velocity tend to be small due to opposing surface mass balance feedback mechanisms (see Section 5). In contrast, in the model the rate of retreat was sensitive to the choice of the calving factor, α. Changing α affected the timescale of retreat but had little impact on the rate at which ice was delivered to the terminus. Consequently the terminus restabilized at similar locations, but with different surface elevation profiles (especially at low elevations), over a range of calving factors (results for α = 1.2 and α = 1.3 are shown in Figs 4b and c). Thus, processes that limit a glacier's rate of retreat may actually increase the total volume loss from the glacier over long timescales (decades to centuries) due to high ice fluxes being sustained over longer periods of time. (An alternative perspective is that a calving parameterization that predicts calving rates that are too high/low may correctly predict locations of terminus stand stills but incorrectly predict changes in glacier volume.)

The model did not exhibit clear relationships between calving rate and geometric variables. For example, although calving rates appeared to be linearly correlated with water depth at the terminus (or grounding line, if the terminus is afloat) (see Brown and others, 1982; Pelto and Warren, 1991) during the initial stages of retreat (Figs 6a–d), the relationship broke down as the terminus retreated through the overdeepening (van der Veen, 1996; Vieli and others, 2001). The model also produced large variations in terminus height-above-buoyancy during retreat (Figs 5 and 6c), which is inconsistent with the original height-above-buoyancy calving criterion (van der Veen, 1996, 2002). The modeled calving rate is, however, linearly related to terminus height-above-buoyancy during much of the retreat (as was observed during the initial stages of the retreat of Columbia Glacier; van der Veen, 1996).

Fig. 6. Relationship between calving rate, water depth and ice thickness during a modeled retreat in which the final ELA is 1400 m and α = 1.2. (a)–(c) Temporal variations in calving rate, terminus/grounding line depth and terminus height-above-buoyancy. (d)–(e) Calving rate versus terminus/grounding line depth and versus terminus height-above-buoyancy. Color indicates model year.

4.2. Terminus advance

The mass-flux calving parameterization was, by itself, only capable of producing a few kilometers of terminus readvance into the overdeepening (e.g. Fig. 7) regardless of the magnitude of the climate perturbation or the choice of the calving factor. An initial lowering of the ELA caused the surface elevation and the balance velocity to increase, and thus promoted advance and the growth of a short floating ice shelf. However, as the terminus advanced into deep water, the terminus velocity increased due to a loss of basal resistance near the terminus, and the balance velocity started to decrease due to a lengthening of the ablation zone. The glacier quickly reached a new steady-state, again indicating that the terminus is stable on seaward sloping beds. Advance through the overdeepening was only possible after reducing the longitudinal stress at the terminus (Fig. 8) to account for the growth of a terminal moraine. After an initial adjustment period, the terminus steadily advanced down fjord at a rate of ~10 m a⁻¹ for a few thousand years until reaching the second sill, at which point the rate of terminus advance increased by more than a factor of five. Increasing or decreasing the back stress from the moraine results in advances that are faster or slower, respectively. Due to the simple nature of the moraine parameterization, the terminus did not reach a steady-state on top of the sill at the end of the fjord and instead continued to advance into the ocean.

Fig. 7. Modeled terminus advance created by lowering the ELA from 1400 to 1300 m and using α = 1.2. The ELA decreased linearly with time for the first 20 a and was subsequently held constant. (a) Calving rate, terminus velocity and balance velocity. (b) Rate of length change. (c) Calving flux, terminus flux and balance flux. (d) Rate of volume change.

Fig. 8. Modeled terminus advance created by lowering the ELA from 1400 to 1300 m, using α = 1.2, and increasing the back stress at the terminus by 8 × 10⁵ Pa to simulate the resistance from a moraine shoal. (a) Calving rate, terminus velocity and balance velocity. (b) Rate of length change. (c) Calving flux, terminus flux and balance flux. (d) Rate of volume change. (e) Glacier geometry at t = 0 (dashed curve) and at t = 4760 a.

5. DISCUSSION

5.1. Surface mass balance feedback loops

Climate variations cause changes in both glacier length and thickness. For land-terminating glaciers, glacier volume change is strongly influenced by two fundamental surface mass balance feedback loops (Harrison and others, 2001): (1) a positive feedback loop with surface elevation and (2) a negative feedback loop with glacier length. For example, decreasing the surface mass balance leads to surface lowering and terminus retreat. Surface lowering increases the size of the ablation area, leading to further decreases in mass balance, whereas terminus retreat removes the highest ablation regions of the glacier and acts to limit changes in mass balance. Due to these feedback loops, glacier response to climate variability depends on both the mass balance gradient and the surface slope (Harrison and others, 2001).

These two feedback loops also operate on tidewater glaciers. However, as described in the introduction, tidewater glaciers can undergo large fluctuations in volume during periods of stable climate. This indicates that additional feedback mechanisms must counteract the stabilizing ‘glacier-length’ feedback during both advance and retreat. During retreat, glacier-length and surface elevation are strongly coupled (Fig. 9a) due to well documented dynamic thinning (e.g. Meier and Post, 1987; Pfeffer, 2007). The additional flow-induced thinning easily offsets the negative glacier-length feedback loop and allows for rapid and extensive retreat despite potentially small variations in balance flux and accumulation area ratio (Figs 4 and 9b).

Fig. 9. Variations in (a) glacier-length and mean surface elevation and (b) accumulation area ratio for the retreat scenario in which the final ELA is 1400 m and α = 1.2 (middle column in Fig. 4).

On the other hand, internal glacier-dynamic feedbacks are incapable of explaining sustained tidewater glacier advance. As a terminus advances into deep water, it loses traction with the bed and tends to accelerate, stretch and thin, thus creating a negative (stabilizing) feedback loop with surface mass balance (Fig. 7). As has been suggested in previous studies (e.g. Oerlemans and Nick, 2006; Nick and others, 2007), the development and progradation of a moraine at the glacier terminus may be a critical component of tidewater glacier advance. A wedge of sediment at the terminus provides resistance to flow (Fischer and Powell, 1998), which limits the effectiveness of the glacier-length feedback by promoting upglacier thickening. Similar arguments have been used to suggest that sediment at the grounding line of an ice shelf helps to promote ice sheet thickening and stability against rising sea level (Alley and others, 2007). Since moraine development and progradation occur over long timescales, terminus advance tends to be much slower than terminus retreat (e.g. McNabb and Hock, 2014).

The observed asynchronous behavior of neighboring tidewater glaciers (e.g. Post and Motyka, 1995; Barclay and others, 2001) can thus be explained by considering variations in ice flow, subglacial topography and sediment supply, and the feedback loops associated with them. Both dynamic thinning during retreat and moraine development and progradation during advance have previously been identified as important processes for tidewater glaciers. The modeling work presented here places these processes into a mass-flux perspective that is useful for understanding tidewater glacier response to climate, especially over long timescales, and for interpreting results from tidewater glacier models.

5.2. Thickness-based calving criteria

The mass-flux perspective of the tidewater glacier cycle provides a means for assessing the behavior of various other calving parameterizations. As a demonstration, here I compare and contrast the behavior of the height-above-buoyancy and crevasse-depth calving criteria. Previous work has shown that models that invoke the height-above-buoyancy criterion are stable on seaward sloping beds but unstable on reverse beds (Vieli and others, 2000, 2001) and can only produce advance through deep water with the incorporation of a moraine at the glacier terminus (Nick and Oerlemans, 2006; Nick and others, 2007). Models that use the crevasse-depth criterion, on the other hand, can produce terminus advance through deep water (without a moraine), and are able to stablize on a reverse bed (Nick and others, 2010). The behavior of these models can be explained in terms of balance velocity, terminus velocity and calving rate.

The height-above-buoyancy and crevasse-depth calving criteria both invoke minimum thickness criteria, H _c. After each model time step the thickness criterion is evaluated and, if the minimum thickness is not exceeded, the terminus is retreated back to the point at which the terminus thickness equals H _c.

Using observations from Columbia Glacier, van der Veen (1996, 2002) first proposed a height-above-buoyancy calving criterion in which the terminus was always 50 m above-buoyancy. That choice of a thickness criterion only works for thick glaciers; Vieli and others (2000, 2001) therefore modified the criterion by replacing the minimum height-above-buoyancy with a small fraction q of the terminus flotation thickness. Taken together, the thickness criterion becomes

(18) $${H_{\rm c}} = (1 + q)\displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}D + {H_0},$$

where H ₀ is a minimum height-above-buoyancy. In the original height-above-buoyancy criterion q = 0 and H ₀ = 50 m, and in the modified height-above-buoyancy criterion q = 0.05 and H ₀ = 0.

Although the height-above-buoyancy calving criterion is able to produce some of the important features of tidewater glacier behavior, it does not allow for the formation of floating ice shelves. In an attempt to resolve this issue, Benn and others (2007a, b) proposed an alternative, the crevasse-depth calving criterion, in which the terminus freeboard (height above sea level) must exceed the crevasse-depth d. The thickness criterion is therefore

(19) $${H_{\rm c}} = D + d.$$

The crevasse depth is calculated by assuming that the base of a field of crevasses is located where the tensile stress and hydrostatic pressure from water in water-filled crevasses balances with the ice overburden pressure (Nye, 1957), giving

(20) $$d = \displaystyle{{{{\sigma ^{\prime}}_{xx}}} \over {{\rho _i}g}} + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}},$$

where ρ _f is the density of fresh water and d _w is the depth of water in a crevasse. Thus the thickness criterion becomes

(21) $${H_{\rm c}} = D + \displaystyle{{{{\sigma ^{\prime}}_{xx}}} \over {{\rho _i}g}} + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}}.$$

Nick and others (2010) later modified the crevasse-depth criterion to include the formation of basal crevasses. With some rearranging of their equations for crevasse-penetration depths, the modified crevasse-depth calving criterion becomes

(22) $${H_{\rm c}} = D + \displaystyle{{{{\sigma ^{\prime}}_{xx}}} \over {{\rho _i}g}} + \left( {\displaystyle{{{\rho _{\rm w}} - {\rho _i}} \over {{\rho _i}}}} \right)\displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}}.$$

This relationship is identical to the original crevasse-depth criterion, except that the thickness criterion is less sensitive to changes in the depth of water in crevasses, which is consistent with model parameters and results from Nick and others (2010). I will therefore limit this discussion to the original crevasse-depth criterion. Substituting the longitudinal deviatoric stress at the glacier terminus given by Eqn (16) into Eqn (21) gives

(23) $${H_{\rm c}} = D + \displaystyle{1 \over 2}\left( {{H_{\rm c}} - \displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}\displaystyle{{{D^2}} \over {{H_{\rm c}}}}} \right) + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}}.$$

Solving for H _c yields

(24) $${H_{\rm c}} = D + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}} \pm D\sqrt {{{\left( {1 + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}\displaystyle{{{d_{\rm w}}} \over D}} \right)}^2} - \displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}}, $$

which is real-valued when

(25) $${d_{\rm w}} \ge D\displaystyle{{{\rho _i}} \over {{\rho _{\rm f}}}}\left( {\sqrt {\displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}} - 1} \right) \approx 0.054D.$$

When Eqn (25) is an equality, the thickness criterion becomes

(26) $${H_{\rm c}} = D\sqrt {\displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}}, $$

which is less than the flotation thickness. Thus, for low values of d _w, the crevasse-depth criterion will produce unstable advance (also Bassis, 2011). Increasing d _w should increase the thickness criterion, which requires that the third term on the right hand side of Eqn (24) be added to the first two terms. Thus, the thickness criterion is

(27) $${H_{\rm c}} = D + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}{d_{\rm w}} + D\sqrt {{{\left( {1 + \displaystyle{{{\rho _{\rm f}}} \over {{\rho _i}}}\displaystyle{{{d_{\rm w}}} \over D}} \right)}^2} - \displaystyle{{{\rho _{\rm w}}} \over {{\rho _i}}}}. $$

Both the height-above-buoyancy and crevasse-depth calving criteria (Eqns (18) and (27)) depend strongly on the submerged depth of the terminus, D, and therefore the criteria evolve with time. Note that for the height-above-buoyancy criterion, the submerged depth equals the water depth because the terminus never goes afloat. For the crevasse-depth-criterion, the submerged depth equals the water depth when the terminus is grounded and (ρ _i /ρ _w)H _t when the terminus is floating.

In models that implement the height-above-buoyancy criterion, glacier termini tend to be unstable on reverse beds and stable on seaward sloping beds because changes in the thickness criterion always outpace changes in submerged depth (i.e. ∂H _c/∂D = ρ _w/ρ _i > 1; Eqn (18); Fig. 10). When a terminus moves into deep water, either during advance or retreat, (1) the thickness criterion increases more rapidly than the submerged depth and (2) the terminus velocity tends to increase (Figs 4 and 7) while the balance velocity decreases. During advance the balance velocity decreases due to the stabilizing glacier-length feedback, whereas during retreat the balance velocity decreases due to glacier-dynamic feedbacks. (Note that variations in lateral drag can limit the changes in terminus velocity and balance velocity if the terminus advances or retreats through a constriction (Jamieson and others, 2012)). These two changes promote thinning of the terminus below the thickness criterion and act to increase the calving rate. Therefore, a glacier that is retreating into deep water will continue to retreat, while a glacier that advances into deep water (without the assistance of a moraine) will tend to stabilize. Terminus advance or retreat out of deep water has the opposite result.

Fig. 10. Gradient of thickness criteria with respect to submerged terminus depth. A value of q = 0 was used for the height-above-buoyancy criterion, and the water depth in crevasses was set to d _w = 10 m and d _w = 25 m for the crevasse-depth criterion. Dashed lines indicate asymptotes where ∂H _c/∂D becomes negatively infinite, which places a maximum bound on the terminus thickness for those particular choices of d _w.

The crevasse-depth criterion behaves similarly to the height-above-buoyancy criterion when the submerged depth is small (‘small’ is determined by the depth of water in crevasses and corresponds to submerged depths for which ∂H _c/∂D > 1; Fig. 10). For greater submerged depths, however, the crevasse-depth criterion can produce completely different behavior. For example the crevasse-depth criterion can cause glacier termini to stabilize on reverse beds during retreat (Figs 5 and 6 in Nick and others, 2010). When a terminus retreats into sufficiently deep water, the thickness criterion does not increase as rapidly as the submerged depth (Fig. 10) and thus, if the dynamic thinning rate is sufficiently small, the terminus will restabilize. The crevasse-depth criterion also allows glacier termini to advance down deep, seaward sloping beds. The initial rate of advance is severely limited by the fact that the thickness criterion increases 1.5–2 times as quickly as the submerged depth (Fig. 10), which allows for thickening of the accumulation area and limits growth of the ablation area. If the submerged depth becomes sufficiently large, however, the thickness criterion increases less quickly than the submerged depth (∂H _c/∂D < 1) and any increase in submerged depth will cause the glacier to suddenly transition from slow to rapid advance. For example, in the modeling work of Nick and others (2010), in which they modeled glacier advance through an overdeepening with the crevasse-depth criterion, the terminus nearly stabilized on a seaward sloping bed before suddenly transitioning into a state of rapid advance (their Fig. 3); the sharp change in advance rate appears to occur during the transition from small to large submerged depths.

The results presented in this study indicate that, from a mass-flux perspective, tidewater glacier termini should generally be stable on seaward sloping beds and unstable on reverse beds. Thus, thickness-based calving criteria are consistent with mass-continuity arguments so long as the thickness criterion evolves more quickly than the submerged depth (i.e. ∂H _c/∂D > 1). Advance down seaward sloping beds and stabilization on reverse beds occur when ∂H _c/∂D < 1, as is the case for the crevasse-depth calving criterion when the submerged depth is large. A logical refinement of the crevasse-depth calving criterion would therefore be to modify it in a way that ensures that ∂H _c/∂D is always >1.

A consequence of this analysis is that calving parameterizations that appear similar under certain conditions (in this case, when the submerged depth of the terminus is small) can produce different rates of advance or retreat and widely disagree on locations of terminus stabilization (Nick and others, 2010). The mass-flux perspective of tidewater glaciers can provide insights into the fundamental behavior (and differences in behavior) of various calving parameterizations. Such insights are needed in order to place bounds on prognostic tidewater glacier models.

6. CONCLUSIONS

Many studies of tidewater glaciers have focused on the complex processes occurring at the glacier–ocean interface. Here, I adopted a different approach to propose a simple, mass-flux calving parameterization that depends on the terminus velocity, terminus balance velocity and a dimensionless calving factor. The parameterization was developed by considering mass continuity and large-scale changes in glacier geometry that occur during tidewater glacier advance and retreat: advance is associated with thickening and (relatively) slow flow while retreat is associated with thinning and flow acceleration. In the parameterization, the calving rate is more strongly affected by the terminus velocity than by the balance velocity because (1) variations in terminus velocity are more heavily weighted and (2) variations in balance velocity tend to be small due to competing surface mass balance feedbacks. The tight link between ice flow and calving in the calving parameterization is consistent with available data and with previous work (van der Veen, 1996, 2002). The significance of including the balance velocity in the parameterization is that it provides a simple ‘switch’ for the glacier to transition from retreat to advance whenever the terminus velocity becomes greater than or less than the balance velocity, respectively.

The mass-flux calving parameterization was developed from mass-continuity arguments, but it is not physically-based because it required an ad hoc assumption about the relationship between the rate of volume change and the terminus and balance velocities. There is therefore significant uncertainty in the form of the parameterization and in the meaning of the calving factor. Nonetheless, the parameterization provides a new perspective of tidewater glacier dynamics that helps to synthesize previous observations and modeling results. For example, previous work has indicated that tidewater glacier termini tend to be unstable on reverse beds and stable on seaward sloping beds. From a mass-flux perspective, reverse beds are unstable due to positive glacier-dynamic feedbacks that overwhelm a stabilizing glacier-length feedback (a decrease in glacier-length reduces the ablation area and limits the rate and extent of retreat). Terminus retreat down a reverse bed and/or past a channel constriction results in a loss of resistance that causes the terminus velocity to increase until it exceeds the balance velocity, which leads to thinning, further flow acceleration and retreat. Advance up a reverse slope can be viewed as adding resistance to flow, which tends to promote thickening and enable further advance. Seaward sloping beds, on the other hand, tend to be stable due to glacier-dynamic feedbacks acting in the same direction as the glacier-length feedback. Advance down a seaward sloping bed reduces the near-terminus resistance to flow, leading to an increase in terminus velocity that ultimately prevents the accumulation area from thickening. In order to advance into deep water, some process, such as the formation and mobilization of a moraine, must limit the increase in terminus velocity so that the accumulation area can thicken. This suggests that terminus advance into deep water is slave to sediment dynamics, and therefore that glaciers with large sediment fluxes should be able to advance faster and farther into deep water than similar glaciers that form over hard beds. In other words, the time- and length-scales associated with the tidewater glacier cycle may depend strongly on bedrock lithology.

The mass-flux calving parameterization also provides insights into the rates of glacier length change and into the geometric evolution of tidewater glaciers. Model results using the calving parameterization indicated that tidewater glacier retreat is insensitive to the size of the climate perturbation that triggered the retreat (as expected) but quite sensitive to the choice of the calving factor in the parameterization. However, the terminus velocity was insensitive to model parameters and depended mostly on terminus location, and thus (1) the terminus always tended to go afloat and to restabilize in similar locations and (2) slower retreats produced larger changes in total volume due to high ice fluxes being sustained over longer tie periods. The contribution of a tidewater glacier to sea level variability depends on both the distance the glacier advances or retreats and the time that it takes the glacier to reach a new steady-state configuration.

Although the mass-flux calving parameterization intentionally ignores some of the important physics of the glacier–ocean interface, it appears to be a promising avenue for modeling the response of tidewater glaciers to climate and ocean variability. The parameterization is simple, can be applied seamlessly to any calving margin, and produces behavior that is consistent with a variety of observations and model results. By stepping back from the glacier–ocean interface, the mass-flux calving parameterization provides a holistic perspective of tidewater glaciers that should be used to place bounds on model projections and to guide development of more physically-based parameterizations.