Mass-balance parameters derived from a synthetic network of mass-balance glaciers

Abstract

Glacier mass-balance parameters such as the equilibrium-line altitude (ELA) play an important role when working with large glacier samples. While the number of observational mass-balance series to derive such parameters is limited, more and more modeled data are becoming available.Here we explore the possibilities of analyzing such 'synthetic' mass-balance data with respect to mass-balance parameters. A simplified energy-balance model is driven by bias-corrected regional climate model output to model mass-balance distributions for 94 glaciers in the Swiss Alps over 15 years. The modeling results in realistic interannual variability and mean cumulative mass balance. Subsequently model output is analyzed with respect to 18 topographic and mass-balance parameters and a correlation analysis is performed. Well-known correlations such as for ELA and median elevation are confirmed from the synthetic data. Furthermore, previously unreported parameter relationships are found such as a correlation of the balance rate at the tongue with the accumulation-area ratio (AAR) and of the glacier elevation range with the AAR. Analyzing modeled data complements in situ observations and highlights their importance: the small number of accurate mass-balance observations available for validation is a major challenge for the presented approach.

1. Introduction

Continuous mass/energy-balance measurements and the repeated compilation of glacier inventory data are two end members of modern integrated glacier-observing systems (WGMS, 2007; Zemp and others, 2008). The interpretation of mass- and energy-balance measurements provides the basic process understanding of climate/glacier interactions and enables the development of corresponding numerical models to inter- and extrapolate the few measured values to regions and periods without such detailed measurements. Glacier inventories contain the basic regional data to accomplish this task (Haeberli and Hoelzle, 1995; Hoelzle and others, 2007).

The increasing availability of high-resolution digital terrain models (DTMs) now opens promising perspectives to more directly relate mass-balance measurements to regional glacier information and large samples of glaciers (Machguth and others, 2006, 2009). This kind of data combination represents an important step towards the direct coupling of a mass-balance model applied to numerous glaciers with climate model output (e.g. Machguth and others, 2009; Paul and Kotlarski, 2010), even though the uncertainties involved are considerable (Machguth and others, 2008). Furthermore, it opens up the opportunity to model key glacier mass-balance parameters for numerous glaciers from a synthetic mass-balance network. The present paper makes a first attempt in this direction.

Certain parameters derived from direct glacier mass-balance measurements are good indicators of glacier characteristics as a function of climatic conditions. The equilibrium-line altitude (ELA), the accumulation-area ratio (AAR) and both parameters for a zero mass balance (ELA0, AAR0) are, for instance, regularly reported in the Glacier Mass Balance Bulletin of the World Glacier Monitoring Service (WGMS, 2009, and earlier issues). From the graphs in these publications, the mass-balance gradient (Γ) and the balance rate at the terminus (b _t) can be derived. The first is the primary link between average atmospheric conditions, glacier mass turnover and flow. The latter relates to the dynamic response (length change, adaptation to new equilibrium) of glaciers (jóhannesson and others, 1989). Much earlier studies related mean air temperature at the ELA (T_ELA) to the precipitation regime (Ahlmann, 1924; Kotlyakov and Krenke, 1982) and hence to maritime- and continental-type glaciers with their strongly different activity/mass turnover, englacial temperatures and relations to periglacial permafrost and timberline (Shumskiy, 1964; Haeberli and Burn, 2002). In fact, such parameters have proved very useful for analyzing local-topographic to large- scale climatic characteristics of glacier distribution and mass balance (Furbish and Andrews, 1984; Ohmura and others, 1992; Dyurgerov and Bahr, 1999), for application to unmeasured glaciers (Haeberli and Hoelzle, 1995; Hoelzle and others, 2007; Braithwaite and Raper, 2009), as well asfor paleoglaciological reconstructions (e.g. Haeberli and Penz, 1985; Kerschner and others, 2000).

Deriving such general parameters from field observations is laborious and only possible for a few glaciers with long enough mass-balance series. Besides the problem that the small data basis from observations limits the possibilities of statistically sound interpretations, mass-balance measurements also have their sources of uncertainty (e.g. Andreassen, 1999; Fountain and Vecchia, 1999). It is therefore desirable to have additional estimates of mass-balance parameters. To accomplish this, we present results for the Swiss Alps obtained from distributed modeling of a synthetic network of mass-balance glaciers. The mass-balance parameters are derived from the model output, with the experiment being run for balanced-budget conditions and 94 selected Swiss glaciers (Fig. 1), which is much more than the number of glaciers documented by field observations. Furthermore, the output of the spatially distributed model does not require interpolations to the entire glacier as is necessary from stake measurements; thus the synthetic network can be seen as an indirect alternative to the direct way of analyzing measurements. The work presented here, however, is highly experimental and complementary to the irreplaceable direct in situ measurements. It introduces new uncertainties and difficulties that require careful analysis and comparison to previous studies and measurements.

Fig. 1. Model domain with the full DTM. Selected glaciers are in white and theremaining glaciers in dark gray. Crosses denote the centers of the REMO gridboxes. White dots show locations of the MeteoSwiss weather stations used for bias correction (altitude in ma.s.l.): COV = Corvatsch (3315); DAV = Davos (1590); EVO = Evolène (1825); GRI = Grimsel-Hospiz (1980); GSB = Grand St Bernard (2472); GUE = Gütsch (2287); JUF = Jungfraujoch (3580); MOL = Molèson (1972); PIL = Pilatus (2106); ROB = Robiei (1898); SAM = Samedan (1705); SAN = S?ntis (2490); WFJ = Weissfluhjoch (2690); and ZER = Zermatt (1638). For orientation, the Swiss border is shown as a solid line and lakes in light gray. The rectangular box indicates the area shown in Figure 4.

2. Basic Approch

A simplified distributed energy-balance model is applied to alculate the mass-balance distribution from which mass-balance parameters are derived. The design of the mass-balance model excludes any reference to the later derived mass-balance parameters. The model strictly operates on a grid and computes mass balance for each gridcell based on a number of input data, namely a DTM, the glacier perimeter and meteorological data.

In the present work, it is assumed that each glacier has a balanced-budget mass balance and an equilibrium extent. Though such a state is very rare in reality, it is nevertheless assumed here because (1) it is an important theoretical concept in glaciology (e.g. Furbish and Andrews, 1984) and (2) it eases the validation and interpretation of the results. To make this assumption a less theoretical approximation, a model time frame (1970–85) is chosen where glaciers were actually close to a balanced-budget mass balance (WGMS, 2009). Only the cumulative mass balance (Σ B_a) over the entire time frame is assumed to be balanced; interannual variability of mass balance, including positive and negative years, still exists.

Modeled mean annual mass-balance distribution is analyzed with respect to the following mass-balance parameters: ELA, T_ELA, summer (June, July and August) air temperature (T_s,_ELA), precipitation (P_ELA), accumulation calculated over an entire mass-balance year (Acc_ELA), global radiation (S_in,_ELA) at the ELA, AAR, b_t and Γ. In the literature, parameters referring to a balanced-budget mass balance are usually written with the suffix 0 (e.g. ELA₀, AAR₀; cf. Cogley and others, 2011). Here all parameters refer to a balanced budget, so the suffix is omitted. Finally, the mass-balance parameters are analyzed with respect to topographic glacier parameters, in particular: surface area (A), minimum and maximum glacier altitude as well as elevation range of the glacier (z_min, z_max and Δz, respectively), a simple glacier hypsometry index (H) representing the ratio in width between accumulation and ablation area and median (z_med) as well as mid-range (z_mid) glacier elevation.

3. Test Site and Data

The present study is performed for the Swiss Alps (Fig. 1), an area of ∼25 000 km² including a glacierized area of ∼1340 km² in 1973 (Müller and others, 1976). The DTM used is from Swisstopo, down-sampled from originally 25m to 100mresolution and referring approximately to the glacier surfaces in the mid-1980s. The digitized glacier outlines from the Swiss Glacier Inventory of 1973 (Paul, 2007) are used to distinguish ice-free from ice-covered areas, as well as individual ice bodies. Though some fast-reacting mid-sized mountain glaciers advanced over this period, the overall area changes were small (Paul and others, 2004). This justifies the assumption that the 1973 glacier outlines and surface are valid for the entire calculation period.

Simplifications in the model make it impossible to calculate reasonable mass-balance values for all types of glaciers (see Section 4). Consequently, the analysis of mass-balance parameters is performed only for glaciers where reasonable mass-balance values are expected. These glaciers are selected based upon the following conditions: (a) no or little debris cover, (b) no or little influence of avalanches, (c) mass loss restricted to melting and (d) sufficient size (area

>1km²). A set of 94 glaciers were found to meet these conditions. The selected glaciers cover 610 km², ∼50% of the total glacierized area. The mass-balance model is driven from output of the regional climate model (RCM) REMO (Jacob and others, 2001). REMO is chosen because it was previously applied to drive glacier mass-balance models (Machguth and others, 2009; Paul and Kotlarski, 2010), and biases in modeled highmountain climate are analyzed in depth by Kotlarski and others (2010). We use data from an RCM run for 1958–2003, at a spatial resolution of 1/6? (∼18 km) and forced by ERA-40 as well as the operational European Centre for Medium-RangeWeather Forecasts (ECMWF) reanalysis at the boundaries. For RCM bias correction (T and S_in), meteorological observations from 14 high mountain weather stations (Fig. 1) operated by MeteoSwiss are applied. For correction of the precipitation bias, the gridded (∼2 km resolution) precipitation climatology by Schwarb and others (2001) is used. For validation of modeled mass balance we use annual (B _a; 1 October–30 September), winter (B _w; 1 October–30 April) and summer balance (B_s; 1 May–30 September) calculated for 50 Swiss glaciers by a combined approach of modeling and measurements (Huss and others, 2010a, b), as well as observed B _a for nine Alpine glaciers (WGMS, 2007).

4. Methods

4.1. The mass-balance model

The applied glacier mass-balance model is a simplified version of more sophisticated energy-balance approaches. Here we briefly summarize the model; a detailed description is given by Machguth and others (2009).

The model runs at daily steps, and the cumulative mass balance b _c on day t + 1 is calculated for every time-step and over each gridcell of the DTM according to Oerlemans (2001):

(1)

where t is the discrete time variable, Δt is the time-step (86 400 s=1 day), l _m is the latent heat of fusion of ice (334 kJ kg⁻¹) and P _solid is solid precipitation (mw.e.). The energy available for melt (Q _m) is calculated as follows:

(2)

where α is the albedo of the surface, S _in is the global radiation, T is the air temperature (^°C) at 2m above ground and outside the glacier boundary layer, and C ₀ + C ₁ T is the sum of the longwave radiation balance and the turbulent exchange linearized around the melting point (Oerlemans, 2001). In contrast to Machguth and others (2009), bias-corrected RCM data are used to force the model and the calibration of the model is re-evaluated. The calibration is restricted to summer melt since winter mass balance is adjusted iteratively by varying P during the model run as explained in Section 4.3. Best fit of observed and modeled melt during the summer months on 14 Swiss glaciers (Machguth and others, 2009) was achieved at C₁ = 12 W m^-2 K^-1 and C₀ = -45Wm^-2.

The source of accumulation is precipitation (P), and a threshold temperature (T _snow) of 1.5°C in combination with a transition range of 0.5°C (i.e. linear increase of the rain fraction from 0% at 1 °C to 100% at 2°C) is used to distinguish P _solid from rain. Redistribution of snow by wind or avalanches is not considered in the model. Refreezing is also not taken into account (it plays a minor role in the European Alps) and any meltwater and rainfall is immediately removed from the glacier.

Global radiation (S _in) is calculated from potential clear- sky global radiation (S _in,clr) and cloudiness (n). The latter is acquired from the RCM output on a daily basis, whereas S _in,clr is computed in a preprocessing routine according to Iqbal (1983) and Corripio (2003), considering all effects of surface topography including shading and assuming standard atmospheric transmission coefficients for clear-sky conditions. S _in,clr is the sum of diffuse (S _in,clrdir) and direct radiation (S _in,clrdir) which are both preprocessed from the DTM and stored subsequently as 2 × 365 arrays (extent and resolution identical to the DTM) of daily mean S _in,clrdir and S _in,_Clrdir. During the mass-balance model run, S _in of every individual time-step is computed from the corresponding preprocessed grids S _in,clrdif and S _in,clrdir and attenuation of clouds (τ_cl). The latter is derived from the RCM cloudiness at the actual time-step according to τ_cl = 1.0 - 0.233n - 0.415n ² (Greuell and others, 1997).

Glaciers are regarded as debris-free, and depending on the surface characteristics (snow, firn or ice) three different constant values for the surface albedo are used in the model: α_s = 0.72, α_f = 0.45 or α_i = 0.27. While the firn albedo has little influence on the model results, the values chosen for α_s and α_i resulted in good agreement of model results and observations (Machguth and others, 2009) and are thus also used in this study. Accumulated snow is assigned af when its age exceeds 1 year, and after 2 years its albedo is lowered to α _i.

4.2. Downscaling of the RCM data and bias correction

The spatial resolution of the RCM and that of the mass-balance model differ greatly, so the RCM data are downscaled for the mass-balance calculation. The downscaling procedure comprises two steps: (1) the RCM data are interpolated to the resolution of the DTM using interpolation techniques, followed by (2) the application of subgrid parameterizations. A detailed description of both steps as well as a brief theoretical background are given by Machguth and others (2009). The key tasks in step 1 are, on the one hand, to choose interpolation schemes that generate smooth changes from one RCM gridcell to the next because such a pattern is more realistic than abrupt breaks from one gridbox to the next. On the other hand, characteristics of the RCM data, such as mean values and frequencies of events of different magnitude (e.g. wet-day frequency), should be preserved. Through experiments and theoretical considerations, Machguth and others (2009) found that thin- plate splines (TPS) interpolation performs best with respect to the aims of step 1. Consequently, TPS is used here to interpolate at each time-step the corresponding daily RCM fields of T, P and n to the DTM resolution. Prior to the interpolation of T the strong dependence on altitude is removed by reducing T to a standard altitude H₀ = 0 m a.s.l. by means of a temporally and spatially constant altitudinal gradient (atmospheric lapse rate) γ_T = -0.0065 °Cm^-1. As shown in more detail by Machguth and others (2009), the chosen value of γ_T agrees well with the mean RCM lapse rate and is in good agreement with near-surface summer lapse rates in the European Alps (Rolland, 2003). No reduction to a standard altitude is performed for P and n because the RCM data show no significant dependence on altitude.

In step 2, simple subgrid parameterizations are applied to account for the major components of the small-scale influences of the rugged Alpine topography. The influence on T, P and S _in, however, differs, so individual subgrid parameterizations are applied for these variables. In the following the subgrid parameterizations for T and Sin are addressed; the approach for P is explained in the next paragraph in connection with the de-biasing. Subgrid-scale variability of T is addressed by adjusting T from H ₀ to the elevation of the DTM using the lapse rate γ _T. The subgrid-scale variability of S_in is complex and mainly controlled by topographic effects like slope, exposition and shading. Cloudiness also exhibits a strong influence on Sin, but is distributed rather smoothly in space, in particular when daily means or longer time-spans are considered. Hence, the preprocessed grids of clear-sky global radiation account for the topographic subgrid-scale variability while the influence of cloudiness is derived directly from the interpolated fields of n and considers the temporal variability. Full details of the method, including a comparison to S_in modeled by the RCM, are given by Machguth and others (2009).

The downscaled RCM fields require additional bias correction for accurate mass-balance calculations (Machguth and others, 2009). Consequently we developed and applied specific approaches for bias removal in T, S_in and P. De-biasing of the downscaled fields of T and S _in is based on comparison and adjustment to observations at the 14 high-mountain weather stations. Precipitation is corrected by scaling the precipitation field to match a high-resolution precipitation climatology Here we use the 2 km resolution precipitation map from Schwarb and others (2001) which is the most detailed currently available reference dataset based on records from >6000 rain gauges. Schwarb and others (2001) applied the interpolation method of Daly and others (1994) to obtain spatially variable precipitation gradients (γ _P ) from the rain-gauge records. Thus, the precipitation scaling provides at the same time the subgrid parameterization including γ_P (cf. step2 above) and the de-biasing. Full details of the bias correction methodology for all three variables are given in the Appendix.

4.3. Iterative precipitation adjustment

Despite all efforts to bias-correct model input, it is not possible to achieve satisfactory agreement with observed mass balances on a glacier-by-glacier basis. This is not only because we assume that all glaciers have an identical cumulative mass balance, but will also result when variability between the glaciers is considered: on the one hand, no current mass-balance model is able to capture all relevant processes; on the other hand, input variables are simply not known with sufficient accuracy. Even after bias correction, precipitation is considered the most uncertain variable because of the well-known difficulties in measuring solid precipitation in high-mountain environments (e.g. Sevruk, 1985, 1997). Furthermore, previous studies using the Schwarb and others (2001) dataset for glacier mass-balance modeling found that at the elevation of glaciers the data require adjustment (e.g. Zemp and others, 2007) by a factor of up to two (Huss and others, 2009). Consequently, we decided to tune P to achieve 'observed' mass balance.

The precipitation adjustment is performed individually for each modeled glacier to achieve a cumulative mass balance of 0mw.e. over the calculation period. As already mentioned, only the cumulative mass balance for the period 1970-85 is forced to be zero; variability of annual mass balance still exists. The iterative precipitation adjustment starts with the calculation of cumulative mass balance in a first model run. For each glacier a first multiplicative precipitation adjustment (M _P) is estimated by comparing model outcome to the assumed Σ B _a = 0m w.e. Subsequently, after each iteration, M_P is corrected until for each glacier a cumulative mass balance of 0mw.e. with a tolerance of ±0.2m w.e results.

4.4. Deriving topographic and glacier mass-balance parameters

The topographic glacier parameters A, z _min, z _max as well as Δz are derived from the DTM and the digitized glacier outlines at 100 m spatial resolution. Glaciers are divided into 50 m elevation bands (z _i) where the index i refers to the respective interval. Mid-range glacier elevation is defined as z _mid = (z _max - z _min)/2, and median glacier elevation as (WGMS, 1989). Furthermore we calculate a simple hypsometry index (H) from the ratio of mean A_i of the accumulation and ablation area. The latter two are divided by z_med because this parameter is highly correlated with the ELA (Braithwaite and Raper, 2009) and using z _med makes the computation of H independent of prior knowledge of the mass-balance distribution. If there are fewer than five elevation bands in the accumulation or ablation area, H is not calculated. H is intended to be a first-order estimate of the ratio of glacier width in the accumulation and ablation areas; the higher H the stronger the difference in width. Thereby glacier width at a specific elevation i is approximated with A _i. A more accurate hypsometry index would require considering the surface slope, but here we prefer a simpler and more widely applicable index.

Mass-balance parameters are derived from the modeled grid of mean annual glacier mass-balance distribution at 100m spatial resolution. The AAR is calculated from the ratio of gridcells with positive and negative mass balance. Mass-balance profiles are defined by calculating mean mass balances for all z _i. The ELA is defined as the elevation where the mass-balance profile equals 0 m w.e. Where this is true for more than one elevation, a mean value is calculated (this rare phenomenon is mainly induced by variability of solar radiation and can occur on steep north-facing glaciers with complex topography). Subsequently, all cells are selected that are located within ±25 m difference in elevation of the ELA, and meteorological conditions at these cells are averaged to obtain T _ELA, P _ELA, Acc_ELA and S _in,ELA. Mass-balance gradients for ablation and accumulation area (Γ_abl and Γ_acc, respectively) are calculated from linear regressions of the mean mass balances of the elevation bands, where the latter are weighted according to their areas. If there are fewer than five elevation bands in the accumulation or ablation area, the corresponding gradient is not calculated. Subsequently the balance ratio Γ_ratio = Γ_abl/Γ_acc is calculated (Furbish and Andrews, 1984). For the case that Γ_acc → 0, Γ_ratio would become undefined. Since in this study Σ B _a ≡ 0, Γ_acc are always greater than 0 (minimum value Γ_acc = 0.125) because otherwise ablation would not be balanced by accumulation. The balance rate at the tongue is derived from the regression function for Γ_abl and the elevation of the tongue (z _t), where the latter is defined as the mean z of the lowest three elevation bands.

4.5. Validation of the synthetic glacier mass-balance network

In Figure 2a, modeled mean B _s, B _w and B _a are compared to the mean measured mass balances of nine Alpine glaciers (Austria: Hintereisferner, Kesselwandferner, Sonnblickkees, Vernagtferner; France: Glacier de Saint-Sorlin, Glacier de Sarennes; Italy: Ghiacciaio del Careser; Switzerland: Griesgletscher, Silvrettagletscher; cf. WGMS, 2007) and modeled mass balances for 50 Swiss glaciers (Huss and others, 2010a, b). Linear regressions of annual values from Huss and others (2010a, b) (in parentheses WGMS, 2007) and our results give R² = 0.80(0.85) for B _a, 0.86 for Bs and 0.64 for Bw. The correlation coefficient between WGMS (2007) and Huss and others (2010a, b) is R ² = 0.92 for B_a . The slightly higher correlation of B _a between the WGMS and the Huss data is to be expected, because the latter use a mass-balance model that is driven from weather station data and calibrated for each individual glacier against different observational data using several tuning parameters (Huss and others, 2010a). Given the fact that the present study makes direct use of RCM data and the only glacier-specific tuning parameter is M _P, the difference in agreement with the WGMS data is small. Mean values for B _s, B_w and B _a are listed in Table 1. Obviously the absolute values of B _w and B _s in our model are slightly reduced compared to Huss and others (2010a, b). The WGMS database holds continuous records of B _s and B _w only for two Alpine glaciers (Vernagtferner and Glacier de Sarennes), so no mean values were calculated. The cumulative mass balances shown in Figure 2b reveal differences between the three datasets: Σ B _a in 1985 is negative according to WGMS (2007), but close to zero according to this study and Huss and others (2010a, b). The agreement of the latter two is due to the assumption Σ B _a = 0 mw.e. and the related precipitation correction applied in this study. Interestingly, until 1976, Σ B _a from WGMS (2007) agrees better with Huss and others (2010a, b), while from 1977 to 1981 interannual variability is more similar to the present study.

Fig. 2. Comparison of modeled mass-balance values (‘94 gl’) to the data from WGMS (2007) (‘9 gl’) and Huss and others (2010a, b) (‘50 gl’): (a) B _a, B _w and B _s and (b) Σ B _a.

Table 1. Comparison of mean values of summer, winter and annual balance over the calculation period, related standard deviations (σ) and final cumulative mass balance according to WGMS (WGMS, 2007), the Huss studies (Huss and others, 2010a, b) and this study. All data are in m w.e.

For Silvretta and Gries glaciers, continuous mass-balance observations exist for the 1970-85 period, and mass-balance profiles at 100m vertical resolution are reported in WGMS (2008) as well as Glaciological Report (1992, and earlier issues). Figure 3 compares 1970-85 measured and modeled mean mass-balance profiles for the two glaciers as well as standard deviations of mass balance of the 100 m elevation intervals. In the present study we investigate balanced-budget glacier parameters, so we assume Σ B _a = 0 m w.e. Because the observed 1970-85 mass balance was -0.21 mw.e. for Gries glacier and 0.09 mw.e for Silvretta (WGMS, 2008) and to ease comparison of measured and modeled mass-balance profiles, the measured profiles have been horizontally shifted by 0.21 and -0.09 mw.e., respectively. The comparison shows that for both glaciers the profiles generally agree well except for the lowermost elevation band on Silvretta and the uppermost two bands on Gries. In both cases the affected areas are <2.5% of the total glacier area. The reason for the steep increase in ablation near the terminus of Silvretta remains unclear but could be related to local variability of accumulation that cannot be reproduced by the model. On Gries glacier the comparison of the mass-balance profiles in the uppermost elevation bands is hampered by the fact that no stake readings were performed above 3150 m a.s.l. (cf. Glaciological Report, 1992, and earlier issues). Standard deviations of modeled and measured mass balance are similar at most elevations, and the observed general increase of standard deviations towards the terminus is well reproduced by the model.

Fig. 3. Comparison of 1970–85 mean modeled and measured WGMS (2008) mass-balance profiles at 100mvertical resolution for (a) Silvretta and (b) Gries glacier. The standard deviations of measured and modeled mass balance for each elevation interval are indicated with horizontal bars.

5. Results

5.1. Mass-balance and topographic parameters

Modeled mean annual mass-balance distribution for the Aletsch region is shown in Figure 4. Mean modeled annual mass-balance profiles from a selection of 18 glaciers are displayed in Figure 5. On several glaciers (e.g. Findel, Festi, Fiescher) mass balance decreases almost linearly below the ELA while other glaciers show a more discontinuous decrease (e.g. Oberer Grindelwald, Saleina, Plaine Morte). Aletsch, Gorner and Oberer Grindelwald even show a pronounced increase in mass balance near the tongue, due to reduced radiation at the glacier tongues, as discussed in more detail in Section 6. Mass-balance profiles in the accumulation area are more similar, with a smaller gradient in accumulation towards higher elevations. The ELAs cover a considerable range of slightly less than 1 km, ranging from 2540 and 2570ma.s.l. (Blüemlisalp-Uri and Glarnischfirn, respectively) at the maritime northern edge of the Alps to 3450 and 3490 m a.s.l. (Weingarten and Hohbarg, respectively) in the dry interior parts of the Valaisan Alps. The large range in ELAs facilitates the following statistical parameter analysis.

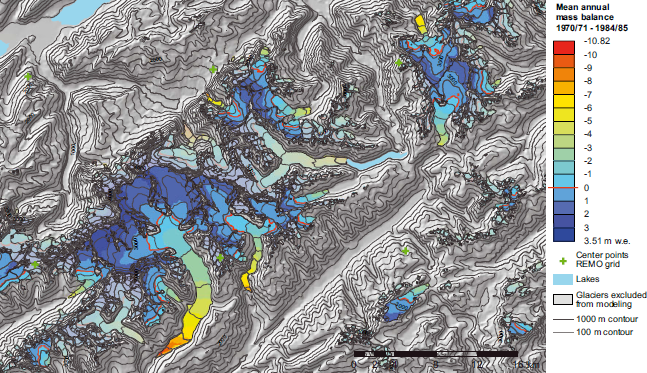
Fig. 4. Modeled mean annual mass-balance distribution (1970–85) for the region around Great Aletsch glacier. Mass-balance distribution for other glaciers than the selected 94 glaciers is shown with lighter colors. Background hillshading is derived from the swisstopo DEM also used for the modeling.

Fig. 5. Mean modeled mass-balance profiles (1970–85) for 18

selected glaciers.

Interannual variability of mass-balance profiles is illustrated for Great Aletsch in Figure 6. The profiles are mostly parallel, with the exclusion of certain years (e.g. 1981). The difference between the most positive and most negative years is largest near the tongue and below the ELA and is smallest in the uppermost accumulation area.

Fig. 6. Annual modeled mass-balance profiles for Great Aletsch glacier. The inverted mass-balance gradient at low elevations is in the model a result of strong shading on the narrow tongue located in a gorge.

Table 2 lists minimum, maximum and mean values as well as standard deviations of the 18 parameters and MP that have been derived from the DTM and the glacier polygons or from the modeled mass-balance distribution and the meteorological input fields. Note that all mass-balance parameters refer to a balanced-budget mass balance and the suffix 0 is omitted (e.g. AAR instead of AAR₀) as explained in Section 2. The ELA is on average 23 m lower than z_mid, but the standard deviation of the latter is somewhat larger. Mean ELA is overestimated by 60 m from z_med while the standard deviation is smaller. Average AAR is 0.59 with a standard deviation of 0.07. There is one remarkable outlier with an AAR of only 0.35 which is Plaine Morte, a large (9 km²) and flat plateau glacier with a weakly developed north-facing tongue. The low AAR is explained by the small mass-balance gradient over most of the ablation area (Fig. 5), resulting from a flat surface topography in the accumulation area with a smooth transition to the north-exposed ablation area. The continuously increasing slope towards the north leads to a reduction of solar radiation compensating for higher temperatures at decreasing elevations.

Table 2. Mass-balance and topographic parameters and M _P derived from mean annual mass-balance distribution and meteorological conditions; averaged over all 94 modeled glaciers and including the standard deviation (σ)

5.2. Correlation matrix

For all parameters listed in Table 2, the correlation coefficients (R) for linear fits x = β₀ + β₁y are displayed in a correlation matrix (Table 3). For most of the parameter correlations |R| ≥ 0.25, and the null hypothesis of parameters being uncorrelated can be rejected at the 0.01 level. However, statistical significance is considered to be of limited relevance here because the sample size is large and significance does not tell whether a relationship is sensible or can be transferred to reality. To make the correlation analysis comprehensible and verifiable, the regression coefficients β₀ and β₁ are listed in Table 4. Furthermore, a selection of six parameter pairs is depicted as scatter plots in Figure 7. For comparison to the model results, Figure 7b shows a number of glacier-specific observed relationships of T _{s ELA} and P _ELA available for the European Alps and Scandinavia (Ohmura and others, 1992).

Table 3. Correlation matrix (R) for linear regression of mass balance and topographic parameters as well as M _P of all 94 modeled glaciers.Correlation coefficients |R| ≥ 0.25 indicate a statistically significant correlation on the 0.01 level. Entries with |R| ≥ 0.58 (corresponds to R ² ≥ 0.33) are in green; entries with |R| ≥ 0.81 (corresponds to R ² ≥ 0.66) are in red

Table 4. Regression coefficients for linear regression x = β ₀ + β ₁ y of mass balance and topographic parameters as well as M_P of all 94 modeled glaciers. The coefficent β₀ is given above the identity and β₁ below identity. All coefficients are calculated with the parameter more to the left on the horizontal axis being the regressor (x) and the parameter more to the right being the dependent variable (y) (e.g. z _med = 701.08 + 0.7760z _mid)

Fig. 7. Scatter plots for six selected parameter pairs. Because of its special characteristics, Plaine Morte (PM) is marked in all plots except (c) and (d): no H and Γacc was calculated for Plaine Morte because its accumulation area spans less than five elevation bands. Dotted lines indicate regressions excluding Plaine Morte. Marmolata glacier (M) is marked in (b).

The correlation values provide a first general characterization of the dependencies among the investigated parameters. Of course, many of them are intrinsically clear or long known and do not require detailed explanation: Highest correlations are found between ELA and z _med (Fig. 7a) and b _t and Δz, followed by ELA and z _mid as well as P _ELA and T _s,_ELA (Fig. 7b). The two meteorological variables P _ELA and T _s,_ELA are closely related because ablation is an increasing function of air temperature, accumulation is an increasing function of P and by definition ablation equals accumulation at the ELA. Interestingly, regressing Acc_ELA to T _ELA and T _{s ELA} yields lower correlations than regressing P _ELA to the two aforementioned parameters. While certain correlations are lower than expected (e.g. Γ_abl, Γ_acc and H show generally intermediate or low correlations; cf. Fig. 7c and d), other correlations are unexpectedly high or even new: for example, Δz is highly correlated with b _t (a correlation was expected but less pronounced) while the high correlation of AAR with b _t or Δz are novel results (Fig. 7e and f). Furthermore z _max and z _min have opposite signs in their correlation with certain parameters and have intermediate or small correlations with any of the meteorological parameters, whereas z _mid, z _med and ELA are all highly correlated with them. Then b _t has much lower correlations with the meteorological parameters than AAR, which is somewhat unexpected since b _t is more directly related to meteorological conditions. While the mass-balance gradient in the accumulation region Γ_acc has intermediate correlation with P _ELA or Acc_ELA, Γ_abl does not show the often-mentioned correlations with T _ELA and P _ELA. The intermediate correlations of P _ELA and Acc_ELA with z _max appear illogical at first sight, and explanations must be sought in the specific topography of the Swiss Alps rather than in the glacier-climate relationship. Finally S _in,_ELA and M _p show only weak correlations with all other parameters. We attempt to explain expected but also unexpectedly high or low correlations in the following section and we hope that the results shown in the two matrices will encourage more detailed investigations in further studies.

6. Discussion

To determine how much the present modeling study is transferable to reality is challenging, because it is difficult to achieve realistic meteorological model input, and validation suffers from considerable uncertainty in observed mass balance and the small sample size of measured glaciers. Furthermore, the definitions of certain mass-balance parameters (e.g. b _t, Γ_abl, Γ_acc) given in the literature (e.g. Cogley and others, 2011) are not detailed enough for the purpose of this study. Consequently it was necessary to develop methods for parameter retrieval as described in Section 4. Nevertheless a number of similarities but also a few differences were found between the synthetic glacier network and other data:

• Modeled mass balance is close to the data from WGMS (2007) and Huss and others (2010a,b), with both winter and summer balance being in a realistic range (Fig. 2). However, there is some disagreement between the two datasets used for validation that could be related to the different glacier samples and methods applied.

• The balanced-budget AAR is 0.59, with a standard deviation of 0.07. On the one hand, an often used value is 0.67 for Alpine-type glaciers (Gross and others, 1976; Braithwaite and Müller, 1980). This value was derived from mass-balance observations on a small number of glaciers in the eastern Alps (Gross and others, 1976). On the other hand, Bahr (1997) calculated a mean AAR for Alpine-type glaciers of 0.58 based on theoretical considerations. This value is supported by Dyurgerov and others (2009), who derived a mean AAR of 0.58 from a worldwide sample of 86 series of mass-balance observations. The 13 Alpine series included have the same mean AAR and a standard deviation of 0.09.

• The mean modeled ELA is very similar to mid-range and median glacier elevation (Table 2). The same is true when mid-range and median glacier elevation are compared to observed ELAs on valley glaciers (Braithwaite and Raper, 2009). Cogley and McIntyre (2003) also found a good agreement of mid-range glacier elevation with ELA.

• The modeled annual mass-balance profiles (Fig. 6) show a maximum variability in the ablation area and a reduced variability in the accumulation area. This pattern agrees with observations on Alpine glaciers (Kuhn, 1984) and is also confirmed by the comparison of modeled and measured mass-balance profiles in Figure 3.

• The observed five relationships of T _{s ELA} and P _ELA from the Alps (Ohmura and others, 1992) fit well into the relationship modeled here (Fig. 7b) and indicate a realistic glacier-climate relationship at the ELA. However the number of observations from the Alps is limited and they cover a much smaller range of T _s,ELA and P _ELA conditions than the model results. There is one clear outlier (Marmolata glacier) in the observations. Because this north-exposed glacier is flat and neither subject to strong shading nor fed by avalanches, we suspect that the observed Marmolata values are erroneous.

• Notably, mean M_P for all glaciers is 1.18 ± 0.38 (one std dev.), supporting the suggestion of Schwarb and others (2001) that their precipitation climatology for gauge undercatch in high-mountain terrain be corrected by a factor of 1.15-1.3.

The modeled Γ_abl (Table 2) seem low compared to previous studies (e.g. Aletsch glacier: modeled 0.76 m (100 m)^-1; cf. 1.0 m (100 m)^-1 according to measurements from 1950/51 and 1951/52 (Haefeli, 1962)). One reason is the small mass-balance gradients at the glacier tongues (Figs 5 and 3a). Reduced mass-balance gradients are observed in reality (see Oerlemans, 2001, for a selection of observed mass-balance profiles), but are usually less pronounced than in the model, where strong shading on glacier tongues located in gorges is considered realistically, while the important effect of enhanced longwave radiation from the rock walls is neglected (cf. Machguth and others, 2009). On the one hand, the possibly underestimated Γ_abl might be one reason that this parameter does not show a higher correlation with other parameters. On the other hand, an overestimation of b_t would be the main reason for the low Γ_abl but b_t shows all the expected correlations. Furthermore, mean B _s and B _a are both slightly underestimated (Table 1). In the comparison the glacier samples are different and both datasets (this study and Huss and others, 2010a, b) rely, although to a differing degree, on a mass-balance model. Nevertheless, this could indicate that modeled mass-balance gradients and hence also mass turnover are somewhat too low.

6.1. Analysis of parameter correlations

A high correlation of b _t with AAR was found (Fig. 7f). The reason is related to the influence of glacier-specific hypsometry on AAR (Furbish and Andrews, 1984): glaciers with long, narrow tongues reach further down and require a higher AAR to balance larger mean melt over their ablation area. A correlation between the hypsometry index and AAR was indeed observed (Fig. 7d) but is not strong. The two most remarkable outliers, with H > 4, are upper Grindelwald glacier (H = 6.7) and Glacier du Trient (H = 4.9). In both cases the ELA separates a gently sloping and wide accumulation area from a narrow and very steep tongue. H is calculated in a simple way where the effect of surface slope on the area per elevation interval is neglected. It remains to be tested if a more comprehensive description of hypsometry would result in a higher correlation with AAR. For instance, using modeled ELA instead of z_med to calculate H results in a higher R ² (0.39) for the correlation with AAR but the H thus derived depends on prior knowledge of mass-balance distribution and cannot easily be applied to unmeasured glaciers.

The rationale behind Δz and b_t being better correlated than b_t and z _min is that Δz = 2(z _mid - z _min) and Γ_abl Δz/2 ≈ b _t because z_mid is a good indicator of ELA (e.g. Haeberli and Hoelzle, 1995; Braithwaite and Raper, 2009) and Γ_abl does not vary strongly among the different glaciers (Table 2). In other words Δz is a good measure of the vertical distance between ELA and the tongue. Haeberli and Hoelzle (1995) assessed melt at the tongue according to b _t = Γ_abl(z _mid - z _min), and from analyzing observational data Dyurgerov and Bahr (1999) concluded that z _mid - z _min is better correlated to b _t than z _min. The reason that z _min is less indicative is that the balance rate at a given elevation varies strongly from more maritime to more continental glaciers.

A novel result is the quite strong positive correlation between Δz and AAR (Fig. 7e). One possible reason for this lies in the, albeit weak, negative correlation of Γ_acc to Δz: A lower Γ_acc means that the glacier tends to have a smaller mean accumulation (calculated over the accumulation area) and thus requires a larger accumulation area to balance melt in the ablation area (cf. Furbish and Andrews, 1984). The linear fit of Δz to AAR provides a 0.5 AAR value for elevation ranges decreasing towards zero (very small glaciers or flat ice caps without outlet glaciers), while values around 0.7 seem to be characteristic of the (largest valley) glaciers with elevation ranges of 1500 m and more. The scatter of about ±0.05 for a given extent in altitude is considerable and most probably related to the hypsographic conditions of individual glaciers. The reasons behind the still remarkable general trend are worth exploring in more detail.

Other interesting relationships are those between Γ_acc and maximum elevation and Γ_acc and precipitation/accumulation (Fig. 7c). On a global scale, Γ_abl is considered dependent on the precipitation regime (e.g. Oerlemans, 2005). In the Swiss Alps, where the range in Γ_abl and P is much smaller than globally, no correlation between Γ_abl and P_ELA was found. This is attributed to the dominance of small-scale effects (cf. Oerlemans and Hoogendorn, 1989). However, in the accumulation area the expected increase in r with increasing precipitation/accumulation at the ELA (cf. Kuhn, 1981; Oerlemans, 2001) was found. In the model simulation, the decrease in Γ_acc with increasing maximum altitude primarily reflects the nonlinear lowering of the sum of positive temperatures. In reality it could also reflect the well-known decrease in precipitation with colder and less humid air temperatures and stronger winds, more easily eroding the drier snow at higher altitudes (cf., for the Alps, Haeberli and Alean, 1985).

The two parameters correlating least with other parameters are M_P (see Section 6.2) and S _{in ELA}. The latter shows only a weak negative correlation with T _ELA and T _s,ELA. The two correlation pairs indicate that glaciers that receive more global radiation (e.g. south-facing glaciers) need lower air temperatures at the ELA (e.g. higher ELAs).

Finally, it must be noted that correlations do not necessarily result from processes in the glacier-climate system (here represented by the mass-balance model), but can also be related to the chosen glacier sample or simply the characteristics of glacier distribution in a certain area. For instance, a negative correlation of z_max with P_ELA is observed (Table 3) which indicates that glaciers at higher elevations are located in drier areas. This is indeed the case in the Swiss Alps, where most of the highest peaks are located in the comparably dry Valais region. Hence, the findings of this study should be applied to other regions only tentatively, as shown by the strong relationship found between T_{s ELA} and P_ELA: Observations from the Alps confirm the model results, but the relationship looks different for Scandinavian glaciers (Fig. 7b). Differences among regions are related to differing climate regimes that determine weights of the components of the energy balance.

6.2. Influence of the precipitation correction on mass-balance parameters

To achieve Σ B _a ≈ 0 m w.e., precipitation is multiplied with a glacier-specific factor M_P . The correction factor is uniform over each glacier's surface, so M_P < 1 will lead to a reduction of the precipitation gradient γ _P and values of M_P > 1 will increase γ _P . The precipitation gradient influences the modeled mass-balance distribution, so there is a potential feedback of the precipitation correction onto mass-balance parameters that needs to be evaluated.

Glacier-specific M_P are correlated to all glacier parameters using linear regression (Table 3). Among the mass-balance parameters a weak correlation was found with AAR and Γ_acc (R² ≈ 0.16) and a moderate negative correlation with P _ELA, T _ELA and Acc_ELA (R² ≈ 0.28). The latter correlations are to be expected, because M_P < 1 always raises the ELA towards colder and drier conditions and vice versa. Furthermore, all parameters that indicate glacier elevation (ELA, z _med, z _mid, z _max) show a weak negative correlation with M_P (R^2≈ 0.15-0.18). There are two possible reasons for this: (1) The mass-balance model could tend to overestimate mass balance at high altitudes, which must be corrected by reducing precipitation through M _P. A possible explanation is the erosion of snow by wind that is not included in the model. On the other hand, the model also excludes refreezing processes which actually enhance accumulation at very high elevations in the Alps. (2) The precipitation climatology from Schwarb and others (2001) overestimates precipitation at high altitudes, and a correction is actually needed. There are almost no reliable precipitation observations above 2700ma.s.l. (Sevruk, 1997) that could reduce uncertainties in the PRISM (Parameter elevation Regressions on Independent Slopes Model) interpolation (Daly and others, 1994) applied by Schwarb and others (2001). Although weak, the dependency of M_p and parameters related to glacier elevation needs further investigation. We conclude that the influence of the precipitation correction on mass-balance parameters is small and has a limited influence on the results of the correlation analysis.

6.3. Implications of the results

In regard to possible applications of geometric inventory data for estimating important glacier and climate variables, relations between information about glacier elevation and ELA, AAR, Γ, b _t and accumulation or precipitation at the ELA are of great interest. The present study again confirms the close correlation between mid-range glacier elevation and ELA for a zero mass balance as already derived from field measurements (Braithwaite and Muller, 1980; Braithwaite and Raper, 2009) and applied to a large numbers of glaciers in entire mountain chains by Haeberli and Hoelzle (1995) and Hoelzle and others (2007). Using mid-range elevation instead of median elevation where hypsographic information is unavailable, introduces a rather small quality reduction in the relation for valley-type glaciers. This important result definitively opens the way for easily estimating balanced-budget ELA values from modern glacier inventory data at regional to continental and even global scales. It also provides a simple and transparent rule of thumb for estimating long-term climate-change impacts on glaciers for everybody, including non-academics: half the change in minimum elevation since the end of the Little Ice Age quantitatively reflects the corresponding rise in ELA since that time or - looking into future scenarios - lower glacier margins will rise to higher elevations by about twice the shift in ELA for a given climate scenario (e.g. a 300 m ELA shift roughly corresponding to a 2°C warming would force the lower glacier margin to rise by ~600 m). The importance of such robust and transparent rules of thumb should not be underestimated: they are most efficient tools for enhancing public awareness of realistic glacier scenarios in a warming world and help avoid grave misunderstandings. They can also serve as plausibility checks in comparison with more complex model approximations, which add information about the timescales involved.

Besides median and mid-range elevation, the vertical glacier extent has a strong predictive potential with respect to important glacier characteristics (cf. Haeberli and Hoelzle, 1995; Dyurgerov and Bahr, 1999; Hoelzle and others, 2007). Its close relation to the balance b _t at the lower glacier margin enables corresponding estimates for unmeasured glaciers without the need to derive them from a distributed mass-balance model for each glacier. Knowledge of typical Γ values from a few glaciers would be sufficient to determine b _t for all of them. In combination with ice thickness estimates from the same vertical extent and overall slope (e.g. Haeberli and Hoelzle, 1995; Paul and Linsbauer, in press), this allows dynamic response times to be estimated. Over time intervals corresponding to such dynamic response times, the mean mass balance can be estimated from the cumulative length change and the total length of a glacier, or, with a view to the future, the length change of a glacier for a given mass-balance scenario (Haeberli and Hoelzle, 1995). It must be kept in mind, however, that b _t is indeed calculated from elevation information, directly depends on the mass-balance gradient and in the real world can be strongly influenced by effects such as albedo changes, debris cover, proglacial lake formation, subglacial ablation or collapse phenomena (Paul and others, 2007). The uncertainty of values estimated for unmeasured glaciers could therefore be considerable.

Fundamentally important relations for practical applications with glacier inventory data are those between air temperature and accumulation/precipitation at the equilibrium line. As first recognized decades ago (Ahlmann, 1924; Kotlyakov and Krenke, 1982; Ohmura and others, 1992), such relations open the possibility of treating large samples of inventoried glaciers as some sort of 'natural precipitation gauges', i.e. estimating regional patterns of precipitation distribution and making realistic approximations of absolute precipitation in high-mountain regions, where direct measurements are difficult, highly uncertain and in most cases simply non-existent. Because of the strong (auto)correlation between summer and annual mean air temperature, the quality loss from substituting the mean annual temperature for the physically more plausible summer temperature remains small. This, in turn, opens other important perspectives, as mean annual air temperature can be related to englacial temperature conditions (Hooke and others, 1983) and to thermal conditions, especially permafrost, in the surrounding areas.

7. Conclusions and Outlook

In this study, we have explored new ways of analyzing output from glacier mass-balance models. We have shown that modeling large glacier samples results in a reasonable mass-balance distribution and glacier parameters derived there from generally agree with the observations. The relationship of 18 glaciological and topographical parameters (and Mp) from 94 glaciers was analyzed in a correlation matrix, revealing dependencies between parameters that were already known from observational data, but also dependencies previously not described (e.g. AAR and b _t, AAR and Δz). The latter deserve further analysis in future work and show the advantage of improved statistics owing to the possibility of modeling a much larger number of glaciers than are measured.

Emphasis was given to choosing a realistic model scenario and to bias correction of the input data. Nevertheless, transferring model results to reality is a critical issue in the approach. Validation is hampered by a lack of observational data and considerable uncertainties therein. The latter also originate from imprecise or missing definitions of mass-balance parameters. However, in contrast to the heterogeneous observational data, the uniform nature of a mass-balance model bears a danger of systematic offset and biases in the output. Although model and observations are mostly consistent, it was shown that in its current version the model tends to underestimate melt at the glacier tongues and there is evidence for too small mass-balance gradients. These points need to be improved in future work.

It was the aim of this study to analyze glacier mass-balance model output in terms of a synthetic mass-balance network and to evaluate its potential to complement observational datasets. In view of the promising results, the approach certainly deserves further attention. Future improvements of the methodology should be made with the mass-balance parameter's field of application in mind. A task specific to mass-balance parameters and equally important to synthetic and observational data will be to comprehensively define important parameters such as the balance rate at the tongue or the mass-balance gradients. Of general importance are improvements to models and input parameters. There is a current trend towards applying glacier mass-balance models to larger glacier samples using different mass-balance models and developing approaches to optimize input data (e.g. Jarosch and others, 2010). Our approach will likely benefit from these efforts. It is envisaged that results of different mass-balance models will be considered and the parameters analysed here will also be investigated in climatologically differing regions and for different glacier geometries (e.g. ice caps). The latter is important because studies working with glacier parameters usually cover extended spatial and temporal domains (e.g. Kerschner and others, 2000; Hoelzle and others, 2007). The lack of observational data will be a permanent issue requiring considerable efforts to be made to maintain a solid link between observations and the model world. This connection is fundamental to the quality of parameters derived from the synthetic networks and highlights the importance of observational data series.