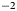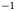Introduction
Pigmented microalgae thrive on glacier and ice-sheet surfaces worldwide (Hoham and Remias, Reference Hoham and Remias2020). They reduce the albedo of snow and ice because their pigments are highly efficient at absorbing solar irradiance (Bidigare and others, Reference Bidigare1993; Duval and others, Reference Duval, Shetty and Thomas1999; Remias and others, Reference Remias, Lütz-Meindl and Lütz2005, Reference Remias2012b; Yallop and others, Reference Yallop2012; Lutz and others, Reference Lutz, Anesio, Field and Benning2015; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020) and they can bloom at high concentrations over large areas (Painter and others, Reference Painter2001; Takeuchi and others, Reference Takeuchi, Dial, Kohshima and Uetake2006; Hisakawa and others, Reference Hisakawa2015; Lutz and others, Reference Lutz2016; Ganey and others, Reference Ganey, Loso, Burgess and Dial2017; Huovinen and others, Reference Huovinen, Ramírez and Gómez2018; Wang and others, Reference Wang, Tedesco, Xu and Alexander2018; Williamson and others, Reference Williamson2018; Cook and others, Reference Cook2020; Gray and others, Reference Gray2021). As a result, microalgae blooms can significantly contribute to surface melt, for example producing $\sim \!10$![]() –13% of run-off in a southwestern site of the Greenland ice sheet (GrIS) (Cook and others, Reference Cook2020) and $\sim \!17$
–13% of run-off in a southwestern site of the Greenland ice sheet (GrIS) (Cook and others, Reference Cook2020) and $\sim \!17$![]() % of snow melt at the Harding Icefield in Alaska (Ganey and others, Reference Ganey, Loso, Burgess and Dial2017).
% of snow melt at the Harding Icefield in Alaska (Ganey and others, Reference Ganey, Loso, Burgess and Dial2017).
Relatively few species are responsible for the albedo reducing effect. Most notable are the dark brown cylindrical algae from the genus Ancylonema (Remias and others, Reference Remias, Holzinger, Aigner and Lütz2012a; Yallop and others, Reference Yallop2012; Di Mauro and others, Reference Di Mauro2020), typically found on ice surfaces and referred to as glacier ice algae, hereafter ice algae; and the green to red spheroidal algae, mostly Sanguina nivaloides and Chloromonas nivalis, typically inhabiting snow and hereafter referred to as snow algae (Remias and others, Reference Remias, Lütz-Meindl and Lütz2005; Lutz and others, Reference Lutz2016; Procházková and others, Reference Procházková, Leya, Křížková and Nedbalová2019). Both types of algae produce their pigments notably to protect their chloroplasts from damage by high irradiance (Bidigare and others, Reference Bidigare1993; Gorton and others, Reference Gorton, Williams and Vogelmann2001; Gorton and Vogelmann, Reference Gorton and Vogelmann2003; Remias and others, Reference Remias, Holzinger and Lütz2009, Reference Remias, Holzinger, Aigner and Lütz2012a) and to melt the surrounding ice and snow crystals to locally create a liquid environment promoting growth (Dial and others, Reference Dial, Ganey and Skiles2018; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020), thereby potentially fostering positive melt feedbacks as growth enhances surface darkening and causes further melting (Lutz and others, Reference Lutz, Anesio, Villar and Benning2014; Ganey and others, Reference Ganey, Loso, Burgess and Dial2017).
In general, algal abundance negatively correlates with surface albedo, but cell concentration alone only explains about half of the observed variance in broadband albedo (BBA) (Thomas and Duval, Reference Thomas and Duval1995; Lutz and others, Reference Lutz2016; Stibal and others, Reference Stibal2017; Cook and others, Reference Cook2020). The remainder may be due to the presence of other light-absorbing particulates (LAPs) such as mineral dust and dispersed cryoconite granules (Takeuchi, Reference Takeuchi2002; Mauro and others, Reference Mauro2017), or changes in the architecture of the snow and ice surface (Tedstone and others, Reference Tedstone2020). In order to isolate the different albedo reducing effects, direct measurements of spectral albedo can be reconstructed using a physically based radiative transfer model (RTM) that represents the different mechanisms impacting the surface albedo, so that the role of each mechanism can be determined. Several such RTMs have incorporated biological LAPs onto cryospheric surfaces, for example the Two-streAm Radiative TransfEr in Snow model (TARTES; Libois and others, Reference Libois2013; Cook and others, Reference Cook, Hodson, Taggart, Mernild and Tranter2017b), the physically based snow albedo model (PBSAM; Aoki and others, Reference Aoki2011) or the Snow, Ice and Aerosol Radiative model (SNICAR, Flanner and others, Reference Flanner, Zender, Randerson and Rasch2007 and BioSNICAR, Cook and others, Reference Cook2020). Most of these models were developed for snow, but Version 4 of SNICAR introduced the representation of ice as a continuous medium with air bubble inclusions, which accurately reproduces the albedo of glacier ice (Whicker and others, Reference Whicker2022). However, none of these models have so far included empirically measured optical properties for intact algal cells, limiting our ability to accurately isolate the albedo reduction associated with algal blooms (Cook and others, Reference Cook2017a).
BioSNICAR calculates biological albedo reduction from cell abundance (cells mL$^{-1}$![]() ) and the optical properties of the cells. These properties are generated from the cell dimensions (${\rm \mu }$
) and the optical properties of the cells. These properties are generated from the cell dimensions (${\rm \mu }$![]() m), cell absorption cross section $A_{\lambda }$
m), cell absorption cross section $A_{\lambda }$![]() (m$^{2}$
(m$^{2}$![]() cell$^{-1}$
cell$^{-1}$![]() ) and the real part of the cell refractive index $n_{\lambda }$
) and the real part of the cell refractive index $n_{\lambda }$![]() (unitless). $A_{\lambda }$
(unitless). $A_{\lambda }$![]() represents the spectral energy absorption for each wavelength $\lambda$
represents the spectral energy absorption for each wavelength $\lambda$![]() per cell and determines the biological contribution to the predicted melt. $n_{\lambda }$
per cell and determines the biological contribution to the predicted melt. $n_{\lambda }$![]() characterizes scattering at the cell membrane and can typically be assumed wavelength-independent (Hart and Leski, Reference Hart and Leski2006; Dauchet and others, Reference Dauchet, Blanco, Cornet and Fournier2015). Both $n_{\lambda }$
characterizes scattering at the cell membrane and can typically be assumed wavelength-independent (Hart and Leski, Reference Hart and Leski2006; Dauchet and others, Reference Dauchet, Blanco, Cornet and Fournier2015). Both $n_{\lambda }$![]() and $A_{\lambda }$
and $A_{\lambda }$![]() are poorly constrained in the model for snow and ice algae and in particular $A_{\lambda }$
are poorly constrained in the model for snow and ice algae and in particular $A_{\lambda }$![]() , which is currently reconstructed using a pigment mixing model (Cook and others, Reference Cook, Hodson, Taggart, Mernild and Tranter2017b; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020). This approach does not account for intracellular effects such as the ‘pigment packaging’ that typically flattens the absorption spectrum of the cells relative to that of their pigments dispersed in solution (Duyens, Reference Duyens1956; Hulst and van de Hulst, Reference van de Hulst HC1981; Morel and Bricaud, Reference Morel and Bricaud1981; Bidigare and others, Reference Bidigare, Ondrusek, Morrow and Kiefer1990; Nelson and others, Reference Nelson, Prézelin and Bidigare1993). This effect may decrease ice algae absorption by $\sim \!25$
, which is currently reconstructed using a pigment mixing model (Cook and others, Reference Cook, Hodson, Taggart, Mernild and Tranter2017b; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020). This approach does not account for intracellular effects such as the ‘pigment packaging’ that typically flattens the absorption spectrum of the cells relative to that of their pigments dispersed in solution (Duyens, Reference Duyens1956; Hulst and van de Hulst, Reference van de Hulst HC1981; Morel and Bricaud, Reference Morel and Bricaud1981; Bidigare and others, Reference Bidigare, Ondrusek, Morrow and Kiefer1990; Nelson and others, Reference Nelson, Prézelin and Bidigare1993). This effect may decrease ice algae absorption by $\sim \!25$![]() % (Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020) and snow algae absorption by up to $\sim \!95$
% (Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020) and snow algae absorption by up to $\sim \!95$![]() % (Halbach and others, Reference Halbach2022).
% (Halbach and others, Reference Halbach2022).
The current lack of in vivo optical properties for snow and ice algae cells in numerical models limits our ability to constrain their effect on snow and ice albedo. This work contributes to upgrading the current state-of-the-art in modelling biological albedo reduction by providing the first empirically measured in vivo optical properties for snow and ice algae and incorporating them into an existing RTM. The algal optical properties are first used to compare the light-absorption efficiency and packaging effect in snow and ice algae cells. Model simulations are then produced to investigate the relative impact of snow and ice algal blooms on the surface albedo of their respective habitats. Finally, model inversions are performed to evaluate the performance of the model in reproducing algal signature from field measurements and estimate the melt generated locally by algal blooms on bare ice surfaces from the southern ablation area of the GrIS.
Methods
Sample collection and processing
Snow and ice surface samples were collected in the ablation area of the southern part of the GrIS (61.1004 N, $-$![]() 46.8470 E; Fig. S1) between 19th July and 9th August 2021 (details in the Supplementary material). They were transported in the dark in cooling boxes to the home laboratory in Denmark and then preserved in a growth chamber (Percival, USA) at $6^{\circ }$
46.8470 E; Fig. S1) between 19th July and 9th August 2021 (details in the Supplementary material). They were transported in the dark in cooling boxes to the home laboratory in Denmark and then preserved in a growth chamber (Percival, USA) at $6^{\circ }$![]() C and with 16:8 h of light:dark cycle (260 ${\rm \mu }$
C and with 16:8 h of light:dark cycle (260 ${\rm \mu }$![]() mol s$^{-1}$
mol s$^{-1}$![]() m$^{-2}$
m$^{-2}$![]() ) until analyses (1–6 weeks after sample collection). Algal cells were then isolated from the samples by density gradient centrifugation and resuspended in clean water (details in the Supplementary material).
) until analyses (1–6 weeks after sample collection). Algal cells were then isolated from the samples by density gradient centrifugation and resuspended in clean water (details in the Supplementary material).
In vivo absorption cross sections: measurements and calculations
Transmission spectra $T_{\lambda }$![]() of three independent pigmented algal suspensions (0.62–2.2 $\times 10^{5}$
of three independent pigmented algal suspensions (0.62–2.2 $\times 10^{5}$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() ) were measured in triplicates in 1 cm pathlength quartz cuvettes (QS101, Hellma Analytics) inserted at the entrance of an integrating sphere mounted in a double beam spectrophotometer (240–850 nm, Shimadzu 2700, 2600-ISR) (details in the Supplementary material). The absorbance (${\rm Abs}_{\lambda }$
) were measured in triplicates in 1 cm pathlength quartz cuvettes (QS101, Hellma Analytics) inserted at the entrance of an integrating sphere mounted in a double beam spectrophotometer (240–850 nm, Shimadzu 2700, 2600-ISR) (details in the Supplementary material). The absorbance (${\rm Abs}_{\lambda }$![]() , m$^{-1}$
, m$^{-1}$![]() ) was then calculated from the transmission spectra as:
) was then calculated from the transmission spectra as:
where $l$![]() is the pathlength of the cuvette, $T_{\lambda , 0}$
is the pathlength of the cuvette, $T_{\lambda , 0}$![]() the transmission spectra of the blank solution (here the cold water used to resuspend the algae) and ${\rm Abs}_{800}$
the transmission spectra of the blank solution (here the cold water used to resuspend the algae) and ${\rm Abs}_{800}$![]() the absorbance at 800 nm to correct for the scattering bias (details in the Supplementary material). 16–25 mL of the solution was then filtered at low pressure onto a pre-weighed GF/F filter of diameter 25 mm (Whatman) that was freeze-dried for biomass quantification (kg$_{\rm dw}$
the absorbance at 800 nm to correct for the scattering bias (details in the Supplementary material). 16–25 mL of the solution was then filtered at low pressure onto a pre-weighed GF/F filter of diameter 25 mm (Whatman) that was freeze-dried for biomass quantification (kg$_{\rm dw}$![]() m$^{-3}$
m$^{-3}$![]() ; Mettler Toledo Analytical Balance AE 260). A 1 mL of the solution was used to perform algal cell counts (cells mL$^{-1}$
; Mettler Toledo Analytical Balance AE 260). A 1 mL of the solution was used to perform algal cell counts (cells mL$^{-1}$![]() ; 1 mL chamber, Marienfeld Superior) placed under a Nikon Eclipse Ti microscope. The absorbance was then normalized to cell counts and dry weight to obtain respectively a cellular absorption cross section ($A_{\lambda }$
; 1 mL chamber, Marienfeld Superior) placed under a Nikon Eclipse Ti microscope. The absorbance was then normalized to cell counts and dry weight to obtain respectively a cellular absorption cross section ($A_{\lambda }$![]() , m$^{2}$
, m$^{2}$![]() cell$^{-1}$
cell$^{-1}$![]() ) and a mass absorption cross section ($A_{\lambda , m}$
) and a mass absorption cross section ($A_{\lambda , m}$![]() , m$^{2}$
, m$^{2}$![]() mg$_{\rm dw}^{-1}$
mg$_{\rm dw}^{-1}$![]() ). Cell sizes (${\rm \mu }$
). Cell sizes (${\rm \mu }$![]() m) and biovolumes (${\rm \mu }$
m) and biovolumes (${\rm \mu }$![]() m$^{3}$
m$^{3}$![]() cell$^{-1}$
cell$^{-1}$![]() ) were measured using a FlowCam (Fluid Imaging Technologies Inc.) and ImageJ (Version 1.53) assuming a spherical shape for snow algae and a circular-based cylinder shape for ice algae (Williamson and others, Reference Williamson2018 after Hillebrand and others, Reference Hillebrand, Dürselen, Kirschtel, Pollingher and Zohary1999; details in the Supplementary material). The algal buoyant density was determined by immersing algae in solutions of Iodixanol (Optiprep, Stem Cell, Proteogenix) of increasing densities until the cells floated. The algal dry densities (kg$_{\rm dw}$
) were measured using a FlowCam (Fluid Imaging Technologies Inc.) and ImageJ (Version 1.53) assuming a spherical shape for snow algae and a circular-based cylinder shape for ice algae (Williamson and others, Reference Williamson2018 after Hillebrand and others, Reference Hillebrand, Dürselen, Kirschtel, Pollingher and Zohary1999; details in the Supplementary material). The algal buoyant density was determined by immersing algae in solutions of Iodixanol (Optiprep, Stem Cell, Proteogenix) of increasing densities until the cells floated. The algal dry densities (kg$_{\rm dw}$![]() m$^{-3}$
m$^{-3}$![]() ) were calculated by multiplying the algal buoyant densities by the dry fraction $x_{\rm dw}$
) were calculated by multiplying the algal buoyant densities by the dry fraction $x_{\rm dw}$![]() (0.59, Gates and others, Reference Gates, Rogerson and Berger1982). The absorption coefficient $a_{\lambda }$
(0.59, Gates and others, Reference Gates, Rogerson and Berger1982). The absorption coefficient $a_{\lambda }$![]() (m$^{-1}$
(m$^{-1}$![]() ) was finally calculated from $A_{\lambda }$
) was finally calculated from $A_{\lambda }$![]() multiplied by the algal dry density and $A_{\lambda , m}$
multiplied by the algal dry density and $A_{\lambda , m}$![]() divided by cell biovolume.
divided by cell biovolume.
In vitro absorption cross sections: measurements and calculations
Pigments were extracted from the GF/F filters used for the biomass quantification described in the previous section, following a procedure adapted from Holzinger and others (Reference Holzinger2018) and Halbach and others (Reference Halbach2022). Briefly, the filters were freeze-dried and preserved at $-80^{\circ }$![]() before analysis when they were broken down by repeating bead-beating (60 s) and flash-frozen in liquid nitrogen three times. The lipophilic and hydrophilic phases were extracted with solutions of respectively methyl tertiary-butyl ether with 0.1% of butylated hydroxytoluene and MeOH 20%. The manipulations were performed under a fume hood in the dark in seven steps until the extracts were not visibly coloured anymore (details in the Supplementary material). The transmission spectra of the extracts were analysed as described in the section above and cellular absorption cross sections were then reconstructed by combining the absorbance spectra of both phases corrected for filtration and extraction volumes and normalizing to cell counts. The percent of purpurogallin in ice algal dry weight was calculated from the concentrations in the hydrophilic extracts (mg L$^{-1}$
before analysis when they were broken down by repeating bead-beating (60 s) and flash-frozen in liquid nitrogen three times. The lipophilic and hydrophilic phases were extracted with solutions of respectively methyl tertiary-butyl ether with 0.1% of butylated hydroxytoluene and MeOH 20%. The manipulations were performed under a fume hood in the dark in seven steps until the extracts were not visibly coloured anymore (details in the Supplementary material). The transmission spectra of the extracts were analysed as described in the section above and cellular absorption cross sections were then reconstructed by combining the absorbance spectra of both phases corrected for filtration and extraction volumes and normalizing to cell counts. The percent of purpurogallin in ice algal dry weight was calculated from the concentrations in the hydrophilic extracts (mg L$^{-1}$![]() ) using the calibration from Halbach and others (Reference Halbach2022) and were then normalized to algal biomass (kg$_{\rm dw}$
) using the calibration from Halbach and others (Reference Halbach2022) and were then normalized to algal biomass (kg$_{\rm dw}$![]() m$^{-3}$
m$^{-3}$![]() ).
).
Calculation and modelling of algal single scattering properties
The distribution of pigments within the cells was assumed homogeneous so that the imaginary part of the refractive index $k_{\lambda }$![]() was directly calculated from the absorption coefficient $a_{\lambda }$
was directly calculated from the absorption coefficient $a_{\lambda }$![]() (m$^{-1}$
(m$^{-1}$![]() , Bohren and Huffman, Reference Bohren and Huffman1983):
, Bohren and Huffman, Reference Bohren and Huffman1983):
The real part of the refractive index $n_{\lambda }$![]() was estimated by optical densitometry following Hart and Leski (Reference Hart and Leski2006) (details in the Supplementary material). The asymmetry parameter $g$
was estimated by optical densitometry following Hart and Leski (Reference Hart and Leski2006) (details in the Supplementary material). The asymmetry parameter $g$![]() and single scattering albedo $w_{0}$
and single scattering albedo $w_{0}$![]() of algae cells were then modelled from the complex refractive index $n_{\lambda } + ik_{\lambda }$
of algae cells were then modelled from the complex refractive index $n_{\lambda } + ik_{\lambda }$![]() of the cells and the cell sizes using the bio-optical model incorporated in the model BioSNICAR. The geometric optics algorithm was chosen for ice algae to represent cells as circular-based cylinder particles (Cook and others, Reference Cook2020), and Mie theory was chosen for snow algae to represent them as spherical particles (Cook and others, Reference Cook2017a).
of the cells and the cell sizes using the bio-optical model incorporated in the model BioSNICAR. The geometric optics algorithm was chosen for ice algae to represent cells as circular-based cylinder particles (Cook and others, Reference Cook2020), and Mie theory was chosen for snow algae to represent them as spherical particles (Cook and others, Reference Cook2017a).
Field spectroscopy and algal abundance measurements
Hemispherical conical reflectance factors (HCRFs) were collected in the study area between 10:00 and 15:20 (solar zenith angle 45–56) using an ASD FieldSpec 4. The spectroradiometer fibre was equipped with a $10^{\circ }$![]() collimating lens held by the arm of a tripod as described in Cook and others (Reference Cook2017a) to avoid self-shading from the instrument. The sensor height was 68–72 cm so that the measurement footprint was $\sim \!0.01$
collimating lens held by the arm of a tripod as described in Cook and others (Reference Cook2017a) to avoid self-shading from the instrument. The sensor height was 68–72 cm so that the measurement footprint was $\sim \!0.01$![]() m$^{2}$
m$^{2}$![]() . The targeted surfaces were chosen to be roughly homogeneous on a wider surface in order to upscale the results for $\sim \!1$
. The targeted surfaces were chosen to be roughly homogeneous on a wider surface in order to upscale the results for $\sim \!1$![]() m$^{2}$
m$^{2}$![]() areas, but are not representative of wider surfaces. Incident radiation was measured using a calibrated Spectralon panel and each spectrum was the average of ten measurements. The spectra were post-corrected for the step at 1000 nm (Painter and others, Reference Painter2001) along with water vapour absorption by polynomial interpolation. For 18 out of 20 spectra, the ice surface was then scraped (1–6 cm) and algal cells were counted as quintuplicates on a full haemocytometer chamber (25 ${\rm \mu }$
areas, but are not representative of wider surfaces. Incident radiation was measured using a calibrated Spectralon panel and each spectrum was the average of ten measurements. The spectra were post-corrected for the step at 1000 nm (Painter and others, Reference Painter2001) along with water vapour absorption by polynomial interpolation. For 18 out of 20 spectra, the ice surface was then scraped (1–6 cm) and algal cells were counted as quintuplicates on a full haemocytometer chamber (25 ${\rm \mu }$![]() L per sample – Fuchs-Rosenthal, Lancing, UK), using an upright field microscope (VisiScope100, Model BL124) with a 100$\times$
L per sample – Fuchs-Rosenthal, Lancing, UK), using an upright field microscope (VisiScope100, Model BL124) with a 100$\times$![]() magnification.
magnification.
Albedo modelling and melt calculations
Albedo modelling was performed using BioSNICAR for two purposes: (a) modelling hypothetical snow and ice surfaces with snow and ice algae blooms to study their relative impact on albedo (parameters in Table S3); and (b) reconstruction of bare ice field HCRF spectra to evaluate the performance of the model in reproducing algal signature and isolate the albedo reducing effect of algal blooms. Because BioSNICAR generates bi-hemispherical albedo, modelled albedo is typically compared to spectral measurements collected using a cosine collector rather than a collimating lens, in order to integrate the back-scattered signal from all directions. This methodology is adapted for snow surfaces but we decided that it was not suitable for the very heterogeneous weathered surface, for the following reasons.
The patches of algae at our specific field site during the fieldwork campaign were rather small, meaning a small footprint was required to ensure the spectrum collected was representative of a homogeneous target surface. However, the signal collected using a cosine collector integrates a signal from a wide surrounding area that differs dramatically from the sampling surface. Reconstructing HCRF spectra with BioSNICAR does mean that we assume either Lambertian scattering or that the narrow nadir view value is representative of the hemispheric value. Evidence in favour of using the HCRF measurements rather than cosine collector albedo measurements are the smaller absolute error between model predictions and our field measurements using the HCRF measurements. We therefore decided that this assumption was more acceptable than assuming surface homogeneity given that we knew the surface to be highly heterogeneous within the cosine collector footprint area. Unfortunately, we cannot provide quantitative estimations of the error from this assumption because we do not know of a reliable way, in the absence of empirical or simulated bidirectional reflectance distribution function (BRDF) or anisotropic reflectance factor data, to gather empirical albedo measurements for our surface types. Since we do not have ice physical and hydrological measurements coupled to the spectra, it was unfortunately not possible to derive a theoretical anisotropy reflectance factor from a model generating BRDF such as DISORT and apply it to our spectra.
We used the adding doubling solver developed by Dang and others (Reference Dang, Zender and Flanner2019) and Whicker and others (Reference Whicker2022), allowing to model glacier ice as a continuum with bubble inclusions (layer type = 1 in the model) and snow as a collection of spherical grains (layer type = 0 in the model). In all cases, we parametrized the model with two layers: (1) a 1 mm upper layer of pure ice (density 917 kg m$^{-3}$![]() ) representing a liquid water film where algal cells were added and (2) an ice/snow layer of varying depth, density and bubble/grain size. The irradiance received by the cells from the ice/snow layer was obtained from the upward flux between the layer of ice/snow and the upper millimetre. The illumination used for all simulations was the default SNICAR direct irradiance ‘mid-latitude winter’ as measurements were collected during cloud-free days. Reconstruction of bare ice HCRF spectra was carried out in two steps, first by inversing the model using a look up table (LUT) to retrieve the ‘clean ice’ background, and second by running the model in forward mode adding algal abundances measured in the field (when available) at the upper surface, with the sampling depth as a free parameter. For the inversion, the model was run to generate 430 080 spectra that were stored in the LUT (details in the Supplementary material). These spectra were then compared to the field spectra in the near infrared wavelengths (NIR, 800–2500 nm), where algae do not influence the spectral signature. The integrated square error between modelled and measured spectra in the infrared spectral range was then computed, and the chosen modelled albedo corresponded to the one yielding the lowest error while being higher in the visible spectrum. The BBA and instantaneous radiative forcing (IRF, J m$^{-2}$
) representing a liquid water film where algal cells were added and (2) an ice/snow layer of varying depth, density and bubble/grain size. The irradiance received by the cells from the ice/snow layer was obtained from the upward flux between the layer of ice/snow and the upper millimetre. The illumination used for all simulations was the default SNICAR direct irradiance ‘mid-latitude winter’ as measurements were collected during cloud-free days. Reconstruction of bare ice HCRF spectra was carried out in two steps, first by inversing the model using a look up table (LUT) to retrieve the ‘clean ice’ background, and second by running the model in forward mode adding algal abundances measured in the field (when available) at the upper surface, with the sampling depth as a free parameter. For the inversion, the model was run to generate 430 080 spectra that were stored in the LUT (details in the Supplementary material). These spectra were then compared to the field spectra in the near infrared wavelengths (NIR, 800–2500 nm), where algae do not influence the spectral signature. The integrated square error between modelled and measured spectra in the infrared spectral range was then computed, and the chosen modelled albedo corresponded to the one yielding the lowest error while being higher in the visible spectrum. The BBA and instantaneous radiative forcing (IRF, J m$^{-2}$![]() s$^{-1}$
s$^{-1}$![]() ) were directly obtained as outputs from the model so that the BBA reduction and the IRF due to algae only were calculated by differentiating the outputs of the clean ice scenario to the ‘algae loaded’ scenario. Daily ice mass loss due to algal cells $\Delta M$
) were directly obtained as outputs from the model so that the BBA reduction and the IRF due to algae only were calculated by differentiating the outputs of the clean ice scenario to the ‘algae loaded’ scenario. Daily ice mass loss due to algal cells $\Delta M$![]() (g m$^{2}$
(g m$^{2}$![]() d$^{-1}$
d$^{-1}$![]() ) was calculated by integrating the algal IRF from the sunrise ($\sim$
) was calculated by integrating the algal IRF from the sunrise ($\sim$![]() 04:00) to sunset ($\sim \!$
04:00) to sunset ($\sim \!$![]() 20:00) with a time step of 15 mn, and dividing by the latent heat of fusion of the ice $\Delta H_{\rm fus}$
20:00) with a time step of 15 mn, and dividing by the latent heat of fusion of the ice $\Delta H_{\rm fus}$![]() (334 J g$^{-1}$
(334 J g$^{-1}$![]() ):
):
The IRF was multiplied by ∆t = 900 s 15 mn$^{-1}$![]() to convert it from s$^{-1}$
to convert it from s$^{-1}$![]() to 15 mn$^{-1}$
to 15 mn$^{-1}$![]() and the 15 min-resolved SZA was retrieved from https://keisan.casio.com/exec/system/1224682277 from the field site coordinates and day of the measurement. Daily mass loss was divided again by the density of water to obtain a volume of meltwater (L m$^{-2}$
and the 15 min-resolved SZA was retrieved from https://keisan.casio.com/exec/system/1224682277 from the field site coordinates and day of the measurement. Daily mass loss was divided again by the density of water to obtain a volume of meltwater (L m$^{-2}$![]() d$^{-1}$
d$^{-1}$![]() ) or by the density of ice to obtain a cm-equivalent melt over a m$^{2}$
) or by the density of ice to obtain a cm-equivalent melt over a m$^{2}$![]() surface (cm w.e. d$^{-1}$
surface (cm w.e. d$^{-1}$![]() ).
).
Results and discussion
Ice algal cells are more efficient light absorbers than snow algal cells
The absorption cross section $A_{\lambda }$![]() of ice algae cells was higher than that of snow algae cells at all wavelengths, and on average $\sim \!2\times$
of ice algae cells was higher than that of snow algae cells at all wavelengths, and on average $\sim \!2\times$![]() higher (Fig. 1a). The ‘uniquely biological’ absorption feature at 670–680 nm, diagnostic of chlorophyll-a was apparent in both snow and ice algae absorption spectra, along with the signature of chlorophyll-b $\sim$
higher (Fig. 1a). The ‘uniquely biological’ absorption feature at 670–680 nm, diagnostic of chlorophyll-a was apparent in both snow and ice algae absorption spectra, along with the signature of chlorophyll-b $\sim$![]() 650 nm for snow algae (Painter and others, Reference Painter2001). The presence of secondary carotenoids in snow algae was demonstrated by a broad absorption band in the 300–600 nm spectral range (Gorton and others, Reference Gorton, Williams and Vogelmann2001; Holzinger and others, Reference Holzinger, Allen and Deheyn2016) and the presence of phenols in snow and ice algae was evidenced by an increasing absorption towards the UV wavelengths (Duval and others, Reference Duval, Shetty and Thomas1999; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020; Halbach and others, Reference Halbach2022). Both algae absorbed broadly across the visible spectral range, maximizing energy harvesting by absorbing strongly where incoming solar energy is greatest. This may have secondary benefits for the algae because most of the energy absorbed is assumed to be conducted to adjacent snow and ice, locally creating a liquid water environment likely promoting growth (Dial and others, Reference Dial, Ganey and Skiles2018; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020).
650 nm for snow algae (Painter and others, Reference Painter2001). The presence of secondary carotenoids in snow algae was demonstrated by a broad absorption band in the 300–600 nm spectral range (Gorton and others, Reference Gorton, Williams and Vogelmann2001; Holzinger and others, Reference Holzinger, Allen and Deheyn2016) and the presence of phenols in snow and ice algae was evidenced by an increasing absorption towards the UV wavelengths (Duval and others, Reference Duval, Shetty and Thomas1999; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020; Halbach and others, Reference Halbach2022). Both algae absorbed broadly across the visible spectral range, maximizing energy harvesting by absorbing strongly where incoming solar energy is greatest. This may have secondary benefits for the algae because most of the energy absorbed is assumed to be conducted to adjacent snow and ice, locally creating a liquid water environment likely promoting growth (Dial and others, Reference Dial, Ganey and Skiles2018; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020).

Fig. 1. Ice and snow algae (a) cellular absorption cross section $A_{\lambda }$![]() , and (b) mass absorption cross section $A_{\lambda , m}$
, and (b) mass absorption cross section $A_{\lambda , m}$![]() . Shaded area corresponds to min. and max. measured coefficients. Microscopy images of (c) ice algae and (d) snow algae from the suspensions analysed.
. Shaded area corresponds to min. and max. measured coefficients. Microscopy images of (c) ice algae and (d) snow algae from the suspensions analysed.
The difference in absorption between the two algae was higher on a per dry mass basis (on average $\sim \!3\times$![]() higher absorption for ice algae; Fig. 1b). This could be due to a higher per cell dry weight of snow algae compared to ice algae (Tables S1 and S2), which is consistent with snow algae typically having a much thicker cell wall and large amounts of lipids associated with their pigments (Remias and others, Reference Remias, Lütz-Meindl and Lütz2005), evidenced by a lower buoyant density for snow than ice algae (1060 vs 1160 kg m$^{-3}$
higher absorption for ice algae; Fig. 1b). This could be due to a higher per cell dry weight of snow algae compared to ice algae (Tables S1 and S2), which is consistent with snow algae typically having a much thicker cell wall and large amounts of lipids associated with their pigments (Remias and others, Reference Remias, Lütz-Meindl and Lütz2005), evidenced by a lower buoyant density for snow than ice algae (1060 vs 1160 kg m$^{-3}$![]() ). We also found that purpurogallin represented $7.1\pm 0.3 \%$
). We also found that purpurogallin represented $7.1\pm 0.3 \%$![]() of the total cellular dry weight of ice algae across three suspensions analysed, which is consistent with previous estimates (Williamson and others, Reference Williamson2018) and $\sim$
of the total cellular dry weight of ice algae across three suspensions analysed, which is consistent with previous estimates (Williamson and others, Reference Williamson2018) and $\sim$![]() 1.75–3.5$\times$
1.75–3.5$\times$![]() higher than for secondary carotenoids in a close relative of snow algae (Hagen and others, Reference Hagen, Grünewald, Xyländer and Rothe2001; Aflalo and others, Reference Aflalo, Meshulam, Zarka and Boussiba2007). The difference in absorption per dry mass could thus also be due to a lower percent of absorbing pigments in the dry mass of snow algae.
higher than for secondary carotenoids in a close relative of snow algae (Hagen and others, Reference Hagen, Grünewald, Xyländer and Rothe2001; Aflalo and others, Reference Aflalo, Meshulam, Zarka and Boussiba2007). The difference in absorption per dry mass could thus also be due to a lower percent of absorbing pigments in the dry mass of snow algae.
We calculated two estimates of the absorption coefficient $a_{\lambda }$![]() from $A_{\lambda }$
from $A_{\lambda }$![]() and $A_{\lambda , m}$
and $A_{\lambda , m}$![]() for each algae (see Methods). These estimates were in excellent agreement (mean error of 2.7 and 9.8% for respectively snow and ice algae; Fig. S2), indicating that the values of $A_{\lambda }$
for each algae (see Methods). These estimates were in excellent agreement (mean error of 2.7 and 9.8% for respectively snow and ice algae; Fig. S2), indicating that the values of $A_{\lambda }$![]() and $A_{\lambda , m}$
and $A_{\lambda , m}$![]() are robust. From $a_{\lambda }$
are robust. From $a_{\lambda }$![]() , we calculated that snow algae cells would have needed a biovolume on average $\sim \!4\times$
, we calculated that snow algae cells would have needed a biovolume on average $\sim \!4\times$![]() higher than ice algae to reach a similar absorption coefficient, assuming a linear relationship between absorption and cell biovolume. This is equivalent to a biovolume of 5748 ${\rm \mu }$
higher than ice algae to reach a similar absorption coefficient, assuming a linear relationship between absorption and cell biovolume. This is equivalent to a biovolume of 5748 ${\rm \mu }$![]() m$^{3}$
m$^{3}$![]() and a cell diameter of $\sim \!22$
and a cell diameter of $\sim \!22$![]() ${\rm \mu }$
${\rm \mu }$![]() m for snow algae. However, among the three algal suspensions that were measured to determine triplicates of $A_{\lambda }$
m for snow algae. However, among the three algal suspensions that were measured to determine triplicates of $A_{\lambda }$![]() (Fig. 1a, Tables S1 and S2), the average cell diameters of snow algae cells were $16.0\pm 2.26$
(Fig. 1a, Tables S1 and S2), the average cell diameters of snow algae cells were $16.0\pm 2.26$![]() , $16.9\pm 3.1$
, $16.9\pm 3.1$![]() and $21.0\pm 5.9$
and $21.0\pm 5.9$![]() ${\rm \mu }$
${\rm \mu }$![]() m and the highest $A_{\lambda }$
m and the highest $A_{\lambda }$![]() was obtained for the solution with the cell diameter of $16.9\pm 3.1$
was obtained for the solution with the cell diameter of $16.9\pm 3.1$![]() ${\rm \mu }$
${\rm \mu }$![]() m. This suggests that $A_{\lambda }$
m. This suggests that $A_{\lambda }$![]() is not linearly positively correlated with cell biovolume and may peak for an intermediate biovolume, which has previously been demonstrated theoretically (Duyens, Reference Duyens1956; Kirk, Reference Kirk1975; Hulst and van de Hulst, Reference van de Hulst HC1981) and empirically (Sathyendranath and others, Reference Sathyendranath, Lazzara and Prieur1987; Bricaud and others, Reference Bricaud, Bédhomme and Morel1988; Stuart and others, Reference Stuart, Sathyendranath, Platt and Irwin1998; Ciotti and others, Reference Ciotti, Lewis and Cullen2002), and attributed to the ‘packaging effect’ (see the next section). In this study, the snow and ice algal cells were of medium size but were collected at the mid to end season and showed a conspicuous dark red (Fig. 1d) and brown (Fig. 1c) pigmentation so that the coefficients $A_{\lambda }$
is not linearly positively correlated with cell biovolume and may peak for an intermediate biovolume, which has previously been demonstrated theoretically (Duyens, Reference Duyens1956; Kirk, Reference Kirk1975; Hulst and van de Hulst, Reference van de Hulst HC1981) and empirically (Sathyendranath and others, Reference Sathyendranath, Lazzara and Prieur1987; Bricaud and others, Reference Bricaud, Bédhomme and Morel1988; Stuart and others, Reference Stuart, Sathyendranath, Platt and Irwin1998; Ciotti and others, Reference Ciotti, Lewis and Cullen2002), and attributed to the ‘packaging effect’ (see the next section). In this study, the snow and ice algal cells were of medium size but were collected at the mid to end season and showed a conspicuous dark red (Fig. 1d) and brown (Fig. 1c) pigmentation so that the coefficients $A_{\lambda }$![]() are likely representative of the highly absorbing cells darkening snow and ice surfaces. Thus, our results suggest that an ice algal cell is a more efficient light absorber than a snow algal cell.
are likely representative of the highly absorbing cells darkening snow and ice surfaces. Thus, our results suggest that an ice algal cell is a more efficient light absorber than a snow algal cell.
Algal pigment absorption is strongly attenuated by a packaging effect, shading intracellular material from high irradiance
Absorption cross sections were reconstructed from pigment extracts for both algae. The typical signatures of secondary carotenoids and phenolics were clearly apparent in the reconstructed coefficients of snow and ice algae respectively (Fig. 2), with an absorption peak $\sim$![]() 464 nm for snow algae (Thomas and Duval, Reference Thomas and Duval1995) and $\sim$
464 nm for snow algae (Thomas and Duval, Reference Thomas and Duval1995) and $\sim$![]() 338 nm for ice algae (Halbach and others, Reference Halbach2022). Differences between the measured and reconstructed absorption cross sections represent the difference between in vivo and in vitro properties, indicating modifications made to the light-absorbing efficiency of the pigment mixture when packaged inside a cell compared to extracted in solution. Here, the reconstructed coefficients were 40 and 5.5 times higher than the in vivo coefficients for snow and ice algae respectively at the absorption peaks, suggesting that a strong intracellular pigment packaging effect flattens the spectral signature of both algae (Duyens, Reference Duyens1956), and of snow algae in particular. This effect arises because the pigments are sufficiently concentrated in the cell that the light is significantly attenuated as it travels through the cell, artificially reducing the effective absorption of the algal pigments (Duyens, Reference Duyens1956). For both algae, this strong packaging effect is consistent with previous suggestions that the large amounts of intracellular pigments are used to ‘shade’ the internal apparatus and protect the cells from damage and overheating (Bidigare and others, Reference Bidigare1993; Gorton and others, Reference Gorton, Williams and Vogelmann2001; Remias and others, Reference Remias, Holzinger, Aigner and Lütz2012a). This effect is especially pronounced when the pigments are abundant (Duyens, Reference Duyens1956; Kirk, Reference Kirk1976; Bricaud and others, Reference Bricaud, Bédhomme and Morel1988), which may explain why snow and ice algal dry densities were significantly higher than green microalgae density ($625\pm 12$
338 nm for ice algae (Halbach and others, Reference Halbach2022). Differences between the measured and reconstructed absorption cross sections represent the difference between in vivo and in vitro properties, indicating modifications made to the light-absorbing efficiency of the pigment mixture when packaged inside a cell compared to extracted in solution. Here, the reconstructed coefficients were 40 and 5.5 times higher than the in vivo coefficients for snow and ice algae respectively at the absorption peaks, suggesting that a strong intracellular pigment packaging effect flattens the spectral signature of both algae (Duyens, Reference Duyens1956), and of snow algae in particular. This effect arises because the pigments are sufficiently concentrated in the cell that the light is significantly attenuated as it travels through the cell, artificially reducing the effective absorption of the algal pigments (Duyens, Reference Duyens1956). For both algae, this strong packaging effect is consistent with previous suggestions that the large amounts of intracellular pigments are used to ‘shade’ the internal apparatus and protect the cells from damage and overheating (Bidigare and others, Reference Bidigare1993; Gorton and others, Reference Gorton, Williams and Vogelmann2001; Remias and others, Reference Remias, Holzinger, Aigner and Lütz2012a). This effect is especially pronounced when the pigments are abundant (Duyens, Reference Duyens1956; Kirk, Reference Kirk1976; Bricaud and others, Reference Bricaud, Bédhomme and Morel1988), which may explain why snow and ice algal dry densities were significantly higher than green microalgae density ($625\pm 12$![]() and $684\pm 12$
and $684\pm 12$![]() kg$_{\rm dw}$
kg$_{\rm dw}$![]() m$^{-3}$
m$^{-3}$![]() for snow and ice algae respectively; 570 kg$_{\rm dw}$
for snow and ice algae respectively; 570 kg$_{\rm dw}$![]() m$^{-3}$
m$^{-3}$![]() for green microalgae; Hu, Reference Hu2004). The stronger packaging effect in snow algae was probably due to a larger biovolume and lower surface to volume ratio than ice algae, which reduces the amount of pigments being reached by non-attenuated light (Kirk, Reference Kirk1976). The absorption peaks in the in vitro spectra were also spectrally shifted in comparison with the in vivo spectra. The peak of phenolics was shifted by $\sim \!12$
for green microalgae; Hu, Reference Hu2004). The stronger packaging effect in snow algae was probably due to a larger biovolume and lower surface to volume ratio than ice algae, which reduces the amount of pigments being reached by non-attenuated light (Kirk, Reference Kirk1976). The absorption peaks in the in vitro spectra were also spectrally shifted in comparison with the in vivo spectra. The peak of phenolics was shifted by $\sim \!12$![]() nm in the ice algal coefficient (from $\sim \!350$
nm in the ice algal coefficient (from $\sim \!350$![]() in vivo to $\sim \!338$
in vivo to $\sim \!338$![]() in vitro) and the chlorophyll-a peak was shifted from $\sim \!675$
in vitro) and the chlorophyll-a peak was shifted from $\sim \!675$![]() to $\sim \!658$
to $\sim \!658$![]() nm in both spectra (Fig. 2). The observed spectral shifts are likely the result of a combination between changes made to the pigment assemblages associated with the pigment extraction process (Berner and others, Reference Berner, Dubinsky, Wyman and Falkowski1989; Bidigare and others, Reference Bidigare, Ondrusek, Morrow and Kiefer1990; Ritchie and Sma-Air, Reference Ritchie and Sma-Air2020) and the effect of the pigment packaging.
nm in both spectra (Fig. 2). The observed spectral shifts are likely the result of a combination between changes made to the pigment assemblages associated with the pigment extraction process (Berner and others, Reference Berner, Dubinsky, Wyman and Falkowski1989; Bidigare and others, Reference Bidigare, Ondrusek, Morrow and Kiefer1990; Ritchie and Sma-Air, Reference Ritchie and Sma-Air2020) and the effect of the pigment packaging.

Fig. 2. Differences in in vivo and reconstructed $A_{\lambda }$![]() for (a) ice algae and (b) snow algae. Shaded area corresponds to min. and max. measured coefficients.
for (a) ice algae and (b) snow algae. Shaded area corresponds to min. and max. measured coefficients.
These results suggest that reconstructing $A_{\lambda }$![]() from pigment extracts overestimates $A_{\lambda }$
from pigment extracts overestimates $A_{\lambda }$![]() and introduces biases in the spectral signature of algae due to spectral shifts. These caveats limit the accuracy of models to predict algal impact on spectral albedo and also prohibit accurate quantification of algae from remote-sensing data because remote quantification relies on the unambiguous detection of pigment signatures.
and introduces biases in the spectral signature of algae due to spectral shifts. These caveats limit the accuracy of models to predict algal impact on spectral albedo and also prohibit accurate quantification of algae from remote-sensing data because remote quantification relies on the unambiguous detection of pigment signatures.
Ice and snow algae blooms have comparable impact on the surface albedo of their respective habitats
The measurements of a$_{\lambda }$![]() along with the real part of the refractive index $n_{\lambda }$
along with the real part of the refractive index $n_{\lambda }$![]() were used to model the single scattering properties of the cells, showing that snow algal cells are more efficient at scattering light (Fig. S3). We then incorporated the optical properties of both algae into a radiative transfer model to compare the albedo lowering efficiency of dark brown ice algal blooms with dark red snow algal blooms. We modelled a wide range of snow and ice albedos (Fig. 3a) and added algal blooms of concentrations between 5 $\times$
were used to model the single scattering properties of the cells, showing that snow algal cells are more efficient at scattering light (Fig. S3). We then incorporated the optical properties of both algae into a radiative transfer model to compare the albedo lowering efficiency of dark brown ice algal blooms with dark red snow algal blooms. We modelled a wide range of snow and ice albedos (Fig. 3a) and added algal blooms of concentrations between 5 $\times$![]() 10$^{3}$
10$^{3}$![]() and $1.5\times 10^{5}$
and $1.5\times 10^{5}$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() (Table S3). The BBA reduction due to ice algal blooms on ice was on average $1.1\pm 0.1$
(Table S3). The BBA reduction due to ice algal blooms on ice was on average $1.1\pm 0.1$![]() times higher than that of snow algal blooms on snow and that ratio decreased with the concentration (from $1.4\pm 0.5$
times higher than that of snow algal blooms on snow and that ratio decreased with the concentration (from $1.4\pm 0.5$![]() at $5\times 10^{3}$
at $5\times 10^{3}$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() to $0.97\pm 0.32$
to $0.97\pm 0.32$![]() at $1.5\times 10^{5}$
at $1.5\times 10^{5}$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() ; Fig. 3b). The impact of carotenoid-rich snow algal blooms on snow albedo is thus almost equivalent to that of heavily pigmented ice algae blooms on ice albedo, despite snow algae being less efficient absorbers and more efficient scatterers. This is due to the different photic conditions in their respective environments (Fig. 3a). Snowpacks are highly scattering environments where the local irradiance field is naturally enhanced at the surface, which increases the probability of absorption by snow algal cells and enhances the impact of snow algae on albedo (Enríquez and others, Reference Enríquez, Méndez and Iglesias-Prieto2005; Ehn and Mundy, Reference Ehn and Mundy2013). This was confirmed by a significant positive relationship between the relative impact of the two algae and the relative irradiance they receive from the ice/snow (${n} = 3\, 149\, 280$
; Fig. 3b). The impact of carotenoid-rich snow algal blooms on snow albedo is thus almost equivalent to that of heavily pigmented ice algae blooms on ice albedo, despite snow algae being less efficient absorbers and more efficient scatterers. This is due to the different photic conditions in their respective environments (Fig. 3a). Snowpacks are highly scattering environments where the local irradiance field is naturally enhanced at the surface, which increases the probability of absorption by snow algal cells and enhances the impact of snow algae on albedo (Enríquez and others, Reference Enríquez, Méndez and Iglesias-Prieto2005; Ehn and Mundy, Reference Ehn and Mundy2013). This was confirmed by a significant positive relationship between the relative impact of the two algae and the relative irradiance they receive from the ice/snow (${n} = 3\, 149\, 280$![]() , ${r}^{2} = 0.88$
, ${r}^{2} = 0.88$![]() , p-value $< 0.001$
, p-value $< 0.001$![]() ; Fig. 3b). In general, snow algal cells receive more light because of their environment (ratio $< 1$
; Fig. 3b). In general, snow algal cells receive more light because of their environment (ratio $< 1$![]() in Fig. 3b) but when the light available to the cells is equal (ratio of 1 in Fig. 3b), ice algae absorb $\sim$
in Fig. 3b) but when the light available to the cells is equal (ratio of 1 in Fig. 3b), ice algae absorb $\sim$![]() 2.7 times more than snow algae at equivalent abundance, because they are more efficient absorbers (Fig. 1).
2.7 times more than snow algae at equivalent abundance, because they are more efficient absorbers (Fig. 1).

Fig. 3. (a) Ranges of clean snow and ice albedos and (b) ratio of BBA reduction from ice algal blooms to snow algal blooms on their respective habitats as a function of algal concentration and the ratio of illumination received by ice algal cells to that received by snow algal cells. Black ticks in (b) indicate average BBA reduction ratio for each algal concentration.
Ice algae blooms locally dropped bare ice albedo by 3.5–43% at our field site, generating 1.2–9.7 L m$^{-2}$ d$^{-1}$
d$^{-1}$
We used the model to reconstruct our bare ice field spectra and prescribed cell concentrations from samples taken at each surface when available (18 spectra out of 20; Table S4). The model recreated these spectra very accurately (Fig. 4; mean standard ${\rm error} = 0.007$![]() (${n} = 20$
(${n} = 20$![]() ), Table S4), and in particular the algal spectral features, including the specific chlorophyll-a peak. The remaining error in the visible spectrum could be related to the uncertainties on the retrieved ice surface properties, or the presence of other LAPs such as mineral dust. Since this error was small, our simulations support previous findings that the dust associated with algal blooms on the GrIS does not significantly lower the albedo above 350 nm (Yallop and others, Reference Yallop2012; Stibal and others, Reference Stibal2017; Cook and others, Reference Cook2020). We also reproduced similar spectra gathered in the dark zone of the GrIS (38 km inland of the margin near Kangerlussuaq in July 2017; Cook and others, Reference Cook2020) and similar agreement between measured and modelled spectra was observed (Fig. S4).
), Table S4), and in particular the algal spectral features, including the specific chlorophyll-a peak. The remaining error in the visible spectrum could be related to the uncertainties on the retrieved ice surface properties, or the presence of other LAPs such as mineral dust. Since this error was small, our simulations support previous findings that the dust associated with algal blooms on the GrIS does not significantly lower the albedo above 350 nm (Yallop and others, Reference Yallop2012; Stibal and others, Reference Stibal2017; Cook and others, Reference Cook2020). We also reproduced similar spectra gathered in the dark zone of the GrIS (38 km inland of the margin near Kangerlussuaq in July 2017; Cook and others, Reference Cook2020) and similar agreement between measured and modelled spectra was observed (Fig. S4).

Fig. 4. Field vs modelled spectra for bare ice surfaces from our field site. Length of scale: 50 cm.
The biological signature in the tested field spectra was exclusively that of ice algae because snow algae concentrations were always low at the sampling sites ($< \!1400$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() ) with a subsequent negligible impact on the BBA. We found that ice algae reduced the surface albedo between 3.5 and 43% at our field site from surfaces where measured concentrations ranged $3\times 10^{3}$
) with a subsequent negligible impact on the BBA. We found that ice algae reduced the surface albedo between 3.5 and 43% at our field site from surfaces where measured concentrations ranged $3\times 10^{3}$![]() –$1\times 10^{5}$
–$1\times 10^{5}$![]() cells mL$^{-1}$
cells mL$^{-1}$![]() , representative of concentrations typically measured on bare ice on the GrIS, although higher concentrations have been measured in the dark zone (Yallop and others, Reference Yallop2012; Stibal and others, Reference Stibal2017; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020). The range of BBA reduction was 0.012–0.099 (Table S4). These results quantify the direct albedo lowering effect of ice algae, which takes into account only the additional absorption of light caused by the presence of the algae. This method allows biological albedo reduction to be isolated from the ice physical configuration, which can change dramatically as the surface ‘weathering crust’ develops and decays, significantly driving the BBA of bare ice surfaces (Tedstone and others, Reference Tedstone2020). Indeed, the BBA of the reconstructed ‘clean ice’ varied by 65%, while the BBA of ‘algal ice’ (i.e. clean ice to which algal concentrations were added in the model) varied by 73% among the 20 spectra. Thus, most of the variability was attributed to the ice structure. This likely explains why we found that field-measured algal counts were not a good predictor of the BBA (${ r}^{2} = 0.20$
, representative of concentrations typically measured on bare ice on the GrIS, although higher concentrations have been measured in the dark zone (Yallop and others, Reference Yallop2012; Stibal and others, Reference Stibal2017; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020). The range of BBA reduction was 0.012–0.099 (Table S4). These results quantify the direct albedo lowering effect of ice algae, which takes into account only the additional absorption of light caused by the presence of the algae. This method allows biological albedo reduction to be isolated from the ice physical configuration, which can change dramatically as the surface ‘weathering crust’ develops and decays, significantly driving the BBA of bare ice surfaces (Tedstone and others, Reference Tedstone2020). Indeed, the BBA of the reconstructed ‘clean ice’ varied by 65%, while the BBA of ‘algal ice’ (i.e. clean ice to which algal concentrations were added in the model) varied by 73% among the 20 spectra. Thus, most of the variability was attributed to the ice structure. This likely explains why we found that field-measured algal counts were not a good predictor of the BBA (${ r}^{2} = 0.20$![]() , $p{\rm }\hbox{-}{\rm value} = 0.06$
, $p{\rm }\hbox{-}{\rm value} = 0.06$![]() , ${ n} = 18$
, ${ n} = 18$![]() , Fig. S5a). The correlation improved when correcting the algal abundance for the sampling depth (Table S4), but remained poor overall (${ r}^{2} = 0.43$
, Fig. S5a). The correlation improved when correcting the algal abundance for the sampling depth (Table S4), but remained poor overall (${ r}^{2} = 0.43$![]() , $p{\rm }\hbox{-}{\rm value} = 0.003$
, $p{\rm }\hbox{-}{\rm value} = 0.003$![]() , ${ n} = 18$
, ${ n} = 18$![]() , Fig. S5b). As a result, a given concentration of ice algal cells can be associated with a wide range of BBAs depending on the ice surface type and the time of the measurement, which is why the algal signature needs to be isolated to estimate algal radiative forcing.
, Fig. S5b). As a result, a given concentration of ice algal cells can be associated with a wide range of BBAs depending on the ice surface type and the time of the measurement, which is why the algal signature needs to be isolated to estimate algal radiative forcing.
We integrated the algal radiative forcing over an entire day yielding melt equivalents of 1.2–9.7 L m$^{-2}$![]() d$^{-1}$
d$^{-1}$![]() . Some 15% of the daily melt produced by the addition of algae was not explained by algal abundance in our model inversions (Fig. S5c). In addition, the ratio of BBA reduction to algal concentration, which represents the algal efficiency in reducing albedo, was almost fully predicted by the illumination received from the ice (${ r}^{2} = 0.93$
. Some 15% of the daily melt produced by the addition of algae was not explained by algal abundance in our model inversions (Fig. S5c). In addition, the ratio of BBA reduction to algal concentration, which represents the algal efficiency in reducing albedo, was almost fully predicted by the illumination received from the ice (${ r}^{2} = 0.93$![]() , p-value $< 0.0001$
, p-value $< 0.0001$![]() , ${ n} = 18$
, ${ n} = 18$![]() , Fig. S5d). This 15% can thus be attributed to the effect of the ice surface that indirectly impacts the biological albedo reduction by changing the photic conditions, as discussed in the previous section. The equivalent surface lowering over a day was 0.13–1.1 cm w.e. d$^{-1}$
, Fig. S5d). This 15% can thus be attributed to the effect of the ice surface that indirectly impacts the biological albedo reduction by changing the photic conditions, as discussed in the previous section. The equivalent surface lowering over a day was 0.13–1.1 cm w.e. d$^{-1}$![]() assuming that the surface is pure ice with a density of 917 kg m$^{-3}$
assuming that the surface is pure ice with a density of 917 kg m$^{-3}$![]() . The density of the weathering crust is however typically lower than pure ice (Cooper and others, Reference Cooper2018), and ice algae were responsible for equivalent surface lowering of 0.17–1.7 cm w.e. d$^{-1}$
. The density of the weathering crust is however typically lower than pure ice (Cooper and others, Reference Cooper2018), and ice algae were responsible for equivalent surface lowering of 0.17–1.7 cm w.e. d$^{-1}$![]() after correcting the surface lowering to the density retrieved by the model for each surface (Table S4). These values are in excellent agreement with previous estimates from the dark zone of 0.03–1.9 cm w.e. d$^{-1}$
after correcting the surface lowering to the density retrieved by the model for each surface (Table S4). These values are in excellent agreement with previous estimates from the dark zone of 0.03–1.9 cm w.e. d$^{-1}$![]() (Cook and others, Reference Cook2020; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020).
(Cook and others, Reference Cook2020; Williamson and others, Reference Williamson, Cook, Tedstone and Anesio2020).
New opportunities
BioSNICAR is now able to reproduce ice algal signature from hyperspectral measurements on bare ice surfaces. This opens up new possibilities to investigate the role of algae on ice melt and in particular, model inversions may enable estimations of the biological albedo reduction from hyperspectral remote-sensing imagery. In addition, the model can now be used to develop algorithms able to predict algal abundance from satellite multispectral imagery, enabling population dynamics to be examined at the regional scale and beyond. However, the error associated with the direct comparison of directional reflectance measurements to hemispherical albedo modelled by BioSNICAR needs to be better constrained, by measuring reflectance from different angles to estimate the BRDF or by deriving the latter from a radiative transfer model with angular definition. We also show that the ice parameters retrieved by BioSNICAR, in particular the density, are consistent with previously published data (Table S4; Cooper and others, Reference Cooper2018). However, empirical measurements of the ice physical properties for each of our sample sites were not available for direct validation of our retrievals. This is a priority research goal that, once completed, will enable our model to be used to investigate the relationships between algal abundance and the physics of the weathered crust and better understand the melting feedbacks between them. Daily surface melt calculations are based on the assumption of constant algal concentration and distribution as well as ice physical configuration throughout the day but they suggest that low algal concentrations can melt more than 1 kg of ice per m$^{2}$![]() per day, which is likely to significantly change the ice physical structure and potentially redistribute algal cells on the surface. These feedbacks are not accounted for in our study and their implementation is an important avenue for future refinements of our model. Finally, coupling BioSNICAR to algal growth, surface mass balance and meteorological models might enable algal albedo reducing effects to be predicted into the future.
per day, which is likely to significantly change the ice physical structure and potentially redistribute algal cells on the surface. These feedbacks are not accounted for in our study and their implementation is an important avenue for future refinements of our model. Finally, coupling BioSNICAR to algal growth, surface mass balance and meteorological models might enable algal albedo reducing effects to be predicted into the future.
Conclusion
We presented the first empirical in vivo optical properties of the two major biological albedo reducers on snow and ice using an integrative approach, accounting for natural variability associated with cell orientation, size, pigment content and packaging effects. Both algae broadly absorbed in the spectral range where solar irradiance peak, suggesting that their pigments allow them to maximize absorption and heat conduction in order create a local liquid environment promoting growth. These pigments also have a photoprotective role as they absorb most of the light passing through the cell, shading the algal internal apparatus behind from damage and overheating. This shading or packaging effect was demonstrated by a strong flattening of the in vivo spectra in comparison with the in vitro spectra, in particular for snow algae. We found that snow algae cells are less efficient absorbers than ice algal cells, yet their blooms had comparable impact on the surface albedo due to the differences in photic conditions of their respective habitats. The reconstruction of bare ice field spectra using the new algal optical properties demonstrated the high efficiency of ice algae in absorbing light and melting ice. At our field site in the ablation zone of the southern GrIS, ice algae populations locally dropped the BBA by between 3.5 and 43%, corresponding to a melt generation of 1.2–9.7 L m$^{-2}$![]() d$^{-1}$
d$^{-1}$![]() . The reconstruction method presented using BioSNICAR allows to isolate and accurately quantify the impact of algal blooms on biological albedo reduction but the error associated with the direct comparison of bi-hemispherical albedo to directional reflectance needs to be better constrained. The method could then be used on remote-sensed hyperspectral data to upscale the estimates presented in this study, in particular in the dark zone of the GrIS where ice algae are blooming on wide areas of the ice surface.
. The reconstruction method presented using BioSNICAR allows to isolate and accurately quantify the impact of algal blooms on biological albedo reduction but the error associated with the direct comparison of bi-hemispherical albedo to directional reflectance needs to be better constrained. The method could then be used on remote-sensed hyperspectral data to upscale the estimates presented in this study, in particular in the dark zone of the GrIS where ice algae are blooming on wide areas of the ice surface.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/jog.2022.64
Data availability
The version 2.0 of the model BioSNICAR used in this work including microalgae optical properties is freely available at https://doi.org/10.5281/zenodo.6390293. Field spectra are available on request at [email protected].
Acknowledgements
This work is part of the project DeepPurple that has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement No. 856416). LC thanks Marie B. Jensen and Laura Perini for the valuable support with field data collection and laboratory manipulations, Pr. Stiig Markager for lending the laboratory instruments and providing useful advices for the bio-optical experiments, as well as L. Schlyter and S. Feng for the map generation.
Author contributions
LC and JC designed the study. LC performed field, modelling and laboratory experiments, analysed the data, produced the figures and wrote the first draft. JC wrote code, produced the model documentation and guided the manuscript preparation and field data collection. LH contributed to data interpretation and guided the pigment extraction. HJ guided the FlowCam and the microscope use and provided useful advice on the experimental design. MT provided helpful guidance on the fieldwork design and refined the manuscript. AA and LB helped with data collection in the field. All authors contributed to the final manuscript.