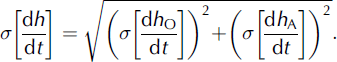Notation

Introduction
The net transfer of land-based ice into the oceans is the second greatest contributor to contemporary sea-level rise after the thermal expansion of ocean water (Reference Braithwaite and RaperBraithwaite and Raper, 2002; Reference Raper and BraithwaiteRaper and Braithwaite, 2006). Between 2001 and 2004, ice caps and alpine glaciers outside Greenland and Antarctica contributed ∼0.77 ± 0.15 mm a−1 to sea-level rise, although the contribution of calving glaciers to this estimate may well be underestimated (Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006; Reference MeierMeier and others, 2007). The Canadian Arctic Archipelago contains the largest glaciated area in the world outside Greenland and Antarctica (Reference Dyurgerov and MeierDyurgerov and Meier, 2005). Although the potential sea-level rise contribution from these ice caps is far less than that from Greenland or Antarctica, their more temperate environs and shorter response times make them potentially more reactive to changes in climate (Reference Raper and BraithwaiteRaper and Braithwaite, 2006).
Although recent estimates of the current sea-level rise contribution of Devon Ice Cap, Nunavut, Canada (75° N, 82° W; Fig. 1) range over an order of magnitude, from 0.003 mm a−1 (Reference Shepherd, Du, Benham, Dowdeswell and MorrisShepherd and others, 2007) to 0.036 or 0.046 mm a−1 (Reference AbdalatiAbdalati and others, 2004; Reference Burgess and SharpBurgess and Sharp, 2004), they agree that Devon Ice Cap is a net contributor to sea-level rise. Laser-altimetry surveys in 1995 and 2000 suggested that the high-elevation region (>1200 m) of the ice cap was thickening by up to 0.20 m a−1, while the low-elevation region (<1200 m) was thinning by up to 0.40 m a−1 (Reference AbdalatiAbdalati and others, 2004). These trends were, however, derived from relatively limited altimetry measurements along two flight-lines that intersect in the western part of the ice cap (Fig. 1; Reference AbdalatiAbdalati and others, 2004). There is therefore a question whether the changes detected by altimetry are representative of the entire ice cap.

Fig. 1. Devon Ice Cap, in the Canadian High Arctic (inset), shown in an orthorectified mosaic of Landsat 7 images acquired in July and August 1999, overlaid with a 1 km digital elevation model (DEM) based on the measurements of Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others (2004). Contour spacing is 100 m, with the 1200 m contour highlighted. The locations of the shallow firn cores (Reference Mair, Burgess and SharpMair and others, 2005: squares; Reference Colgan and SharpColgan and Sharp, 2008: circles) and the approximate NASA altimetry flight-lines are shown (Reference AbdalatiAbdalati and others, 2004).
On the basis of meteorological records from weather stations at Iqaluit, Clyde River and Eureka, thickening of the high-elevation region was originally attributed to anomalously high snowfall during the 1995–2000 period (Reference AbdalatiAbdalati and others, 2004). However, both in situ measurements of surface mass balance (Reference KoernerKoerner, 2005) and reconstructions of net annual snow accumulation on the ice cap derived from shallow firn cores (Reference Colgan and SharpColgan and Sharp, 2008) show that the annual net accumulation rate at high elevations on the ice cap, during the 1995–2000 period, was anomalously low in comparison to the 1963–2003 mean. A number of factors may explain this apparent discrepancy. First, net accumulation, which is measured by mass-balance programs and deduced from ice-core measurements, is different from snowfall, in that melt-induced runoff can potentially remove a fraction of the annual accumulation from any site on the ice cap. Therefore, these two types of records are not strictly comparable. Second, problems with measuring snowfall in polar regions, where precipitation totals are low, trace falls are common and wind redistribution of snow is frequent, are well known (Reference Woo, Heron, Marsh and SteerWoo and others, 1983). Finally, station records of snowfall are typically derived from coastal sites that are often remote from the ice-cap locations in which we are interested.
An alternative explanation of the thickening would be that the rate of firnification on the ice cap was unusually low during the 1995–2000 period, resulting in a reduction in the density of the near-surface snow and firn. However, the ice content of firn deposited in 1995–2000 is anomalously high relative to the 1963–2003 mean, which suggests that the observed thickening is unlikely to reflect anomalously low rates of firn compaction during that period (Reference Colgan and SharpColgan and Sharp, 2008). Thus, if the observed thickening is real, its cause may lie in a recent change in the dynamics of the ice cap.
Mean annual rates of ice-thickness change can be estimated by comparing mean annual net accumulation rates to mean specific outflow rates for individual drainage basins (cf. Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998, Reference Thomas2000). Comparison of these measurements (which have units kg m−2 a−1) with laseraltimetry measurements (m a−1) requires conversion of accumulation rates to thickness changes using an assumed density for the material added to or removed from the ice column. In this study, estimates of rates of thickness change in the high-elevation region of Devon Ice Cap were derived using in situ measurements of annual surface velocity for 11 flux gates aligned along the 1200 m contour. For four of these basins, we compared these estimates with estimates derived using shorter-term, but spatially denser, measurements of surface velocity derived using interferometric synthetic aperture radar (InSAR).
Methods
Surface velocities
The specific ice outflow through each flux gate was calculated using measurements of ice thickness (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004) and ice surface velocities. Seventeen 4 m wooden stakes were installed along the 1200 m contour of the ice cap in April 2005 and re-surveyed in April 2006. Stake locations were determined with Leica Geosystems series 500 dual-frequency global positioning system (GPS) instruments using static differential methods. Multiple base station locations were used to ensure a maximum distance of 25 km between the base station and stake positions during each survey. Data were processed in Leica Geo Office (version 1.0) and achieved phase position solutions accurate to better than ±0.5 cm in the horizontal (x, y) and ±2.0 cm in the vertical (z). At each survey point, the GPS antenna was mounted on top of the stake, and the vertical dimension of the GPS position was corrected to a base-of-stake position to within ±2 cm. For stakes that did not tilt between surveys, the total positional error (the combination of position and manual measurement errors over the two seasons) was estimated to be ±2.5 cm in the x, y and z directions. For stakes 6 and 17, which became tilted between surveys (10° and 20°, respectively), the GPS antenna was mounted on a survey tripod centred over the point where the stake protruded from the snow surface, and trigonometry was used to estimate the base-of-stake position. For these two stakes, the total positional error was estimated as 25% of the trigonometrically corrected horizontal distance in the x and y directions (±8.8 and 2.8 cm, respectively) and 10% of the trigonometrically corrected vertical distance in the z direction (±6.2 and 9.6 cm, respectively). The azimuth and magnitude of annual horizontal stake velocities were computed from the difference in stake positions and the time elapsed between surveys.
Six stakes were lost between 2005 and 2006, which forced a redefinition of the flux gates and resulted in flux gates of unequal width. To compensate for the paucity of repeat GPS measurements in the east of the study region, one ‘dummy’ velocity (derived by InSAR using winter–spring 1996 European Remote-sensing Satellite (ERS-1/2) imagery; Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005) was included with the ten measured stake velocities (Fig. 2).

Fig. 2. (a) The mean annual rate of specific outflow (dh O/dt (mw.e.a−1)). The ten stakes (ST) and one InSAR-derived velocity point (IN) are shown with velocity vectors. Stakes lost between surveys are shown with crosses. (b) The mean annual net accumulation rate (dh A/dt (m w.e. a−1)), based on net accumulation rates at 13 core sites (Reference Mair, Burgess and SharpMair and others, 2005: squares; Reference Colgan and SharpColgan and Sharp, 2008: circles). (c) The mean annual rate of thickness change (dh/dt (m w.e. a−1)).The approximate locations of the NASA laser-altimetry flight-lines are also shown (Reference AbdalatiAbdalati and others, 2004).
Reference Shepherd, Du, Benham, Dowdeswell and MorrisShepherd and others (2007) calculated the specific mass balance of Devon Ice Cap using an approach similar to that adopted here, but they used velocity measurements derived by InSAR rather than stake-derived velocities to compute ice fluxes. Although these InSAR measurements have high spatial resolution, and can identify narrow bands of faster flow within flux gates, they relate to relatively short periods of time (∼30 days) and may not provide reliable estimates of annual average velocities. They also lack true three-dimensional resolution, as only ascending orbit data are available, and they were produced by resolving the satellite-look direction velocities onto the calculated direction of steepest down-glacier slope. The uncertainty in these velocities increases with (1) increasing angle between the ice flow and satellite-look directions (β (°)) and (2) decreasing surface slope. The limitations of these measurements therefore justify the use of stake-based measurements of true annual mean velocities as an alternative means of estimating rates of thickness change.
Drainage basin delineation
The ten velocity stakes and one dummy point were used to define 11 flux gates and the drainage basins that feed them. Stake 12 was not used for this purpose because of its proximity to stake 11. Drainage basins were delineated using a 1 km resolution digital elevation model (DEM) of the ice cap (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004). The flow direction tool in ArcGIS 9.0 was used to compute the flow direction in each DEM cell, based on the DEM slope direction field. Once the flow direction in each DEM cell was known, the upslope source cell of each DEM cell could be identified. Flowlines leading to each stake were then extracted manually from the flow direction field (Reference Le Brocq, Payne and SiegertLe Brocq and others, 2006) by connecting successive upslope source cells from the stake back to the main drainage divide of the ice cap (Fig. 2). Flowlines leading from the stakes to the main drainage divide were used to define the drainage basin boundaries for each flux gate (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998).
Annual specific outflow
To calculate the mean annual specific outflow through a given flux gate, the horizontally averaged surface ice velocity perpendicular to the flux gate (u
G (m a−1)) was calculated as the mean of the perpendicular velocities at either end of the flux gate. The vertically averaged ice velocity through the flux gate
![]() was taken as 0.8 times the horizontally averaged surface velocity on the assumption that flow through each flux gate occurred primarily by ice deformation and that the value of the exponent, n, in Glen’s flow law for ice = 3 (Reference Reeh and PatersonReeh and Paterson, 1988; Reference PatersonPaterson, 1994. Our error analysis uses a ±0.5 range in n values to accommodate threads of fast flow, which influence small portions of some gates (cf. fig. 7 in Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005), causing the n value across a given gate to vary from 3 (see Appendix). The annual volumetric outflow through each gate (V
B (m3 a−1)) was calculated by multiplying the vertically averaged ice velocity by the cross-sectional area of the gate (A
G (m2)), which was determined from ice-thickness values interpolated at 1 km intervals across a given gate (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004). To allow comparison with measurements of net accumulation rate in the basin draining through the flux gate, the volumetric outflow was converted into a rate of specific outflow, equivalent to a surface-elevation change in each basin (dh
O/dt (m w.e. a−1))according to:
was taken as 0.8 times the horizontally averaged surface velocity on the assumption that flow through each flux gate occurred primarily by ice deformation and that the value of the exponent, n, in Glen’s flow law for ice = 3 (Reference Reeh and PatersonReeh and Paterson, 1988; Reference PatersonPaterson, 1994. Our error analysis uses a ±0.5 range in n values to accommodate threads of fast flow, which influence small portions of some gates (cf. fig. 7 in Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005), causing the n value across a given gate to vary from 3 (see Appendix). The annual volumetric outflow through each gate (V
B (m3 a−1)) was calculated by multiplying the vertically averaged ice velocity by the cross-sectional area of the gate (A
G (m2)), which was determined from ice-thickness values interpolated at 1 km intervals across a given gate (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004). To allow comparison with measurements of net accumulation rate in the basin draining through the flux gate, the volumetric outflow was converted into a rate of specific outflow, equivalent to a surface-elevation change in each basin (dh
O/dt (m w.e. a−1))according to:
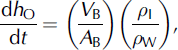
where ρ I is the density of ice, ρ W is the density of water and A B is the area of the drainage basin (m2; Table 1). To allow for the presence of firn in each ice column, we assume an ice density (900 kg m−3) less than that of pure ice (917 kg m−3). By comparing the calculated annual specific outflow with measurements of mean annual net accumulation for 1963–2003 we implicitly assume no change in specific ice outflow over that period. We have no way of assessing the validity of this assumption.
Table 1. The drainage basin area (A
B ± σ[A
B]), flux gate width (d
G), flux gate mean ice thickness
![]() and across-gate InSAR coverage for the 11 drainage basins
and across-gate InSAR coverage for the 11 drainage basins

Annual specific net accumulation
The mean annual change in surface elevation due to net accumulation over the 1963–2003 period (dh A/dt (m w.e.a−1)) was determined for each drainage basin using mean annual net accumulation rates determined from 13 shallow firn cores (Reference Mair, Burgess and SharpMair and others, 2005; Reference Colgan and SharpColgan and Sharp, 2008; Table 2). The mean annual net accumulation rate at each core site was calculated by dividing the water equivalent depth of the 1963 ‘bomb’ layer by the number of years between 1963 and the year the core was recovered. The bomb layer is the result of fallout from atmospheric thermonuclear weapons testing and is easily identified as a layer of high 137Cs activity by down-borehole gamma spectrometry (Reference Dunphy and DibbDunphy and Dibb, 1994). The relationship between mean annual net accumulation and elevation and latitude at each core site was derived using multiple linear regression (MLR; cf. Reference Van der Veen, Bromwich, Csatho and KimVan der Veen and others, 2001):
where Z is the elevation (m) and Y is the Universal Transverse Mercator (UTM) northing (m) (p < 0.01; adjusted r = 0.73 for df = 12; Fig. 3). The standard error of the multiple linear reagresion (MLR) estimate is 0.02 m w.e.a−1, with residuals of up to |0.07| m w.e.a−1, distributed randomly across the high-elevation region (Table 2). The inclusion of longitude as an explanatory variable did not improve the performance of the regression. Equation (2) was used to estimate the mean annual net accumulation rate in each 1 km DEM cell. An area-weighted mean of the estimated net accumulation rates in all gridcells was computed for each basin (Fig. 2).
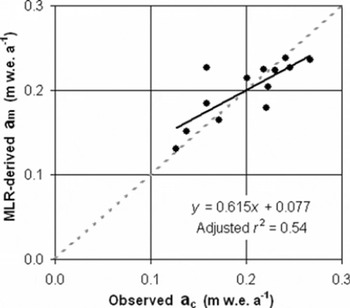
Fig. 3. MLR-derived annual net accumulation rate (a m) versus observed mean annual net accumulation rate (a c) at the 13 core sites (residuals: Table 2). Line y = x is shown for reference (dashed).
Table 2. The observed net accumulation rate (Reference Mair, Burgess and SharpMair and others, 2005; Reference Colgan and SharpColgan and Sharp, 2008), multiple linear regression (MLR) residuals and latitude and longitude of each shallow core site (Fig. 1)

Annual specific rate of thickness change
Several studies have used the mass imbalance approach, in which specific net accumulation and outflow rates are compared, to infer basin-scale rates of thickness change (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998, Reference Thomas2000, Reference Thomas2001). This method assumes that any surplus (deficit) of mass in a given basin will result in an increase (decrease) in the snow surface elevation or ice-cap thickness, rather than an increase (decrease) in the firnification rate. Hence:
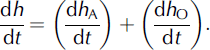
Results of this calculation for the 11 drainage basins are presented in Table 3. For the four gates for which InSARderived across-gate velocity profiles were available (1, 6, 9 and 10), InSAR-derived specific outflows were also compared with calculated specific net accumulation rates to obtain independent estimates of rates of thickness change (Table 4).
Table 3. The in situ-derived mean annual rate of specific outflow (dh O/dt ± σ[dh O/dt]), mean annual net accumulation rate (dh A/dt ± σ[dh A/dt]) and mean annual rate of thickness change (dh/dt ± σ[dh/dt]) for the 11 drainage basins, as well as the area-averaged mean for the entire high-elevation region (Fig. 2)

Table 4. The InSAR-derived mean annual rate of specific outflow (dh O/dt ± σ[dh O/dt]), and its resulting mean annual rate of thickness change (dh/dt ± σ[dh/dt]) for the four drainage basins with good (>80%) InSAR coverage. Differences between InSAR thickness change estimates and in situ estimates are also shown

Results
Basin-scale thickness changes
There is a clear contrast between the in situ derived rates of specific outflow, net accumulation and thickness change in drainage basins south of the main east–west drainage divide (basins 7–11; hereafter southern basins) and the basins north of that divide (basins 1–6; hereafter northern basins). The annual specific outflow from the southern basins (area average: −0.25 ± 0.16 m w.e.a−1) is significantly greater (two-tailed t test assuming equal variance, p < 0.01) than that from the northern basins (area average: −0.12 ± 0.13 mw.e.a−1; Fig. 2). Similarly, the annual specific net accumulation rate in the southern basins (area average: 0.22 ± 0.02 m w.e.a−1) is significantly (p < 0.01) greater than that in the northern basins (area average: 0.18 ± 0.02 m w.e. a−1;Fig. 2). The variation in net accumulation rate is explained primarily by latitude rather than by elevation, leading to a strong north–south net accumulation gradient across the study region (Fig. 2). The rate of thickness change in the northern basins (area average: 0.05 ± 0.14 m w.e. a−1)is significantly (p < 0.05) greater than that in the southern basins (area average: −0.03 ± 0.16 m w.e. a−1; Fig. 2). The area-averaged mean annual rate of thickness change for all 11 basins (0.01 m w.e. a−1)differs from zero by much less than the estimated margin of uncertainty (±0.12 m w.e. a−1; Table 3).
Regression of InSAR-derived velocities against in situ stake velocities yields a slope of 1.04 (r 2 = 0.72, standard error of the estimate = 3.7 ma−1; Fig. 4). The difference between InSAR-derived and measured-stake velocities is, however, variable. The combined effects of β and slope (taken as the quotient of β over slope) account for 41% of the variability in the differences between the measured and InSAR-derived velocities (Fig. 4). The residual variability may result from either differences in the length of the measurement periods or from true changes in surface velocity between the 1996 InSAR observations and the 2005–06 in situ velocity measurements.
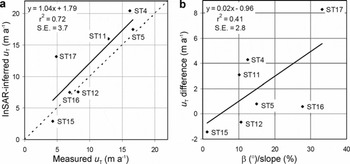
Fig. 4. (a) InSAR-derived downslope surface velocities (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005) regressed against measured stake velocities for the seven stakes for which data are available. Line y = x is shown for reference (dashed). (b) The difference between InSAR-derived and measured stake velocities regressed against the ratio of the angle between the satellite-look and ice-flow directions (β) to surface slope.
There is significant variability within the across-gate InSAR-derived horizontal velocity profiles that cannot be captured by linear interpolation between the stake measurements (Fig. 5). The InSAR-derived specific outflow estimates are always of the same sign as the stake-derived estimates, but they are greater than the stake-derived estimates in basins 1 (−0.59 versus −0.17 m w.e. a−1)and 10 (−0.33 versus −0.25 m w.e. a−1),and less than the stake-derived estimates in basin 6 (−0.08 versus −0.16 m w.e. a−1).The InSAR- and in situ-derived specific outflow estimates are not independent in basin 9, as the single InSAR dummy point used to supplement the stake data was located in this basin (Table 4).

Fig. 5. InSAR-derived across-gate (d G) surface velocity (u G) profiles (points) are compared to the two-point stake velocity profiles (lines) across flux gates 1 (a), 9 (b), 10 (c) and 6 (d).
Discussion
Level of uncertainty
The calculation of uncertainty estimates for the results presented here is explained in the Appendix. Uncertainties in the horizontally and vertically averaged velocities are the main sources of uncertainty in the calculated rates of thickness change. The area-averaged rate of thickness change across all drainage basins (0.01 mw.e.a−1) is much smaller than the associated uncertainty (±0.12 m w.e. a−1),so we find no significant thickness change for the high-elevation region as a whole. However, the calculated rates of thickness change do exceed the associated uncertainty in four drainage basins. Two drainage basins in the northwest (3 and 4) show significant thickening, and two (9 and 11) in the south and east show significant thinning. Reference Shepherd, Du, Benham, Dowdeswell and MorrisShepherd and others (2007) also report positive mass balance in the northwest sector of the ice cap and negative mass balance in the southeast, though their calculations relate to entire drainage basins while ours only relate to regions above 1200 m.
Comparison with laser altimetry
NASA laser-altimetry observations over the high-elevation region suggest a maximum rate of thickening between 1995 and 2000 of 0.20 m a−1,while figure 3 in Reference AbdalatiAbdalati and others (2004) suggests a mean thickening rate of ∼0.05 m a−1. To facilitate a direct comparison between the observed and calculated rates of thickness change, the measurements derived from laser altimetry were converted from an absolute rate of thickness change (m a−1) to an estimated water-equivalent thickening rate (m w.e.a−1). These conversions were performed using two distinct density scenarios: (1) density close to ice (900 kg m−3), which assumes that the observed thickening is the result of decreased ice outflow from the high-elevation region, as suggested by the recent decrease in the annual net accumulation rate and increase in the rate of firnification in the high-elevation regions of the ice cap (Reference Colgan and SharpColgan and Sharp, 2008); and (2) density of fresh snow (300 kg m−3), which assumes that the observed changes are the result of a short-term increase in the accumulation rate during the measurement period (Reference AbdalatiAbdalati and others, 2004). These two scenarios correspond to mean rates of thickness change within the high-elevation region of between ∼0.015 and ∼0.045 m w.e.a−1 . Although these values are substantially greater than the area-averaged rate of thickness change reported in this study (0.01 m w.e.a−1), they do lie within our estimated range of uncertainty (±0.12 m w.e.a−1). When making this comparison however, we recognize that it is difficult to estimate the area-averaged rate of thickness change and its associated uncertainty using data from the two laser-altimetry flight-lines.
Our results do not indicate a widespread thickening trend across the high-elevation region of the ice cap, such as was inferred from the altimetric measurements. Our best estimate of the overall area-averaged thickening rate is within error of zero, and significant thickening is found only in basins 3 and 4. The two laser-altimetry flight-lines provide only partial coverage of the ice cap (Fig. 2) and are biased towards the western portion of the high-elevation region, where we find thickening at a rate much higher than the average for the high-elevation region (0.13 ± 0.03 and 0.01 ± 0. 12 m w.e. a−1, respectively; Table 3). The rates of thickness change observed by laser altimetry over the high-elevation parts of the ice cap range between approximately −0.15 and +0.20 m a−1, but the majority of observations lie between zero and 0.10 m a−1. Only ∼10% of the laseraltimetry observations from the high-elevation region suggest thinning (Reference AbdalatiAbdalati and others, 2004). The altimetry coverage, however, is poor or non-existent in basins 9 and 11, where we find significant thinning. Thus, the differences between our estimated rates of thickness change and those of Reference AbdalatiAbdalati and others (2004) might be due to the difference in the areas sampled in the two sets of measurements.
Ice dynamics
Over short measurement periods, laser-altimeter measurements of ice-thickness change can be strongly influenced by interannual variability in the height of the snow surface (Reference ThomasThomas and others, 2001). However, the laser-altimetry observations of high-elevation thickening of the northwest region of Devon Ice Cap are unlikely to reflect anomalously high net accumulation between 1995 and 2000, because both in situ surface mass-balance measurements (Reference KoernerKoerner, 2005) and ice-core measurements suggest anomalously low net accumulation at high elevations on the ice cap during this period (Reference Colgan and SharpColgan and Sharp, 2008). It is also unlikely that a decrease in the rate of firnification can explain the laseraltimetry observations (Reference ThomasThomas and others, 2001), as the ice content of shallow firn cores recovered from the high-elevation region of Devon Ice Cap increased between 1995 and 2000, relative to the 1963–2003 mean (Reference Colgan and SharpColgan and Sharp, 2008). Increased ice content is more likely to be indicative of more rapid firnification.
We therefore suggest that longer-term trends in ice outflow provide the most likely explanation for the thickening in the northwest region of the ice cap. Decreased ice outflow over time might result from the downwards diffusion of a cold wave associated with Neoglacial cooling in the Canadian High Arctic. As ice deformation is concentrated near the glacier bed, the cooling and stiffening of basal ice reduces the outflow from a basin (Reference Reeh and GundestrupReeh and Gundestrup, 1985). If the Neoglacial cooling of Devon Island began approximately 1050 years BP and peaked approximately 150 years BP (Reference BlakeBlake, 1981), this temperature cycle would have a period of ∼1800 years. The amplitude of such a cycle would reach 5% of its surface value at ∼430 m depth (Reference PatersonPaterson, 1994, p. 204–211). Peak cooling at this depth will lag peak cooling at the surface by ∼860 years. The ice depth in basins 3 and 4 ranges from ∼650 m near the ice divide to ∼250 m at the flux gates (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004). Thus, Neoglacial cooling of basal ice in these basins may have begun only in the last few centuries, and it could account for reduced outflow from these basins.
The calculated thinning in the southern drainage basins (9 and 11) has not been independently validated by laseraltimetry observations. The observed decrease in the net accumulation rate (∼25% after 1989; Reference Colgan and SharpColgan and Sharp, 2008) and inferred increase in the firnification rate may be sufficient to explain the thinning in basin 9, but are probably not sufficient to account for the thinning in basin 11 (−0.24 ± 0.20 m w.e. a−1).Increased ice outflow may therefore be a factor in the thinning of this basin, which is one of three drainage basins in the eastern region of the ice cap where threads of fast flow (and probably basal sliding) extend above the 1200 m contour (fig. 7 in Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005). A possible cause of increased ice outflow is increased meltwater penetration to the glacier bed as a result of recent climate warming (e.g. Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002).
Another factor that must be borne in mind when comparing the two estimates of rates of thickness change is that the estimates pertain to different time periods. We differenced a 40 year mean specific net accumulation rate with a 1 year specific outflow rate to obtain our estimate, while the laser-altimetry observations describe a 5 year mean rate of thickness change. If the specific outflow rate from any sector of the ice cap has changed systematically over the past 40 years, this has implications for the comparison. If the specific outflow has been decreasing relative to specific net accumulation rate (as postulated for northwest basins 3 and 4), then our estimate of the specific outflow will be below the 40 year average and we will have overestimated the 40 year mean rate of thickening. Equally, if specific outflow from basin 11 has been increasing over time, we will have overestimated the rate of outflow and the long-term thinning rate may be less than we have suggested.
Conclusions
The rate of thickness change of the entire high-elevation region of Devon Ice Cap appears to be within error of zero (0.01 ± 0.12 m w.e.a−1). A non-uniform pattern of thickness change across the ice cap is, however, suggested by our observations. We find significant thickening in two drainage basins (basins 3 and 4), and significant thinning in another two (basins 9 and 11). Estimates of the rate of high-elevation thickening derived from laser altimetry are likely to be affected by a spatial bias towards the northwestern region of the ice cap where we find significant thickening. A possible ice-dynamic mechanism to explain the thickening in the northwest high-elevation region of Devon Ice Cap is the downward diffusion of the Neoglacial cooling wave. This may be responsible for a recent stiffening of the basal ice in these basins, and a decrease in outflow. In contrast, meltwater-induced enhancement of already fast ice flow may account for the thinning observed in basins 9 and 11.
Acknowledgements
This work was supported by the Polar Continental Shelf Project (PCSP contribution No. 030-07), the Natural Sciences and Engineering Research Council of Canada (NSERC), the ArcticNet Network of Centres of Excellence, the Canadian Circumpolar Institute (CCI), the Northern Scientific Training Program (NSTP) and the Alberta Ingenuity Fund. We thank the Nunavut Research Institute and the communities of Resolute Bay and Grise Fjord for permission to conduct fieldwork. D. Burgess, F. Cawkwell and S. Williamson assisted with the fieldwork. J. Dowdeswell and T. Benham kindly provided ice-thickness measurements. We also thank W. Abdalati for his thorough review of the manuscript.
Appendix Error Analysis
Traditional error analysis was used to quantify the uncertainty associated with estimates of specific outflow, net accumulation and thickness change. The largest sources of uncertainty in computing the rate of specific outflow for a given drainage basin lie in the calculation of the horizontally and vertically averaged ice velocities. Uncertainty in the vertically averaged velocity
![]() due to the choice of n was taken as the difference between estimates derived assuming n = 2.5 and 3.5 for a given flux gate. Uncertainty in the horizontally averaged velocity (σ
H[u
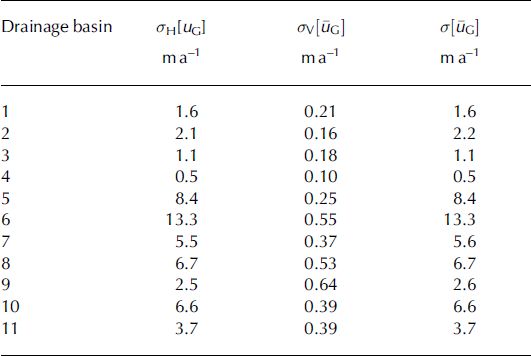
G] (m a−1)) is a function of how well two stakes in a flux gate represent the ‘true’ horizontal surface velocity profile perpendicular to the gate. To quantify this uncertainty, across-gate InSAR velocity profiles (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005; Fig. 5) were linearly detrended and compared with the two-point velocity profiles derived from stakes. The standard error of the differences between the detrended InSAR profile and the two-point profile was taken to represent the uncertainty in the horizontally averaged velocity across each flux gate (σ
H[u
G]; Table 5). The standard errors are relatively low for gates that do not contain threads of fast-flowing ice (e.g. 1.6 m a−1 for gate 1), but much higher for those flux gates within which fast flow does occur (e.g. 6.6 and 13.3 m a−1 for flux gates 10 and 6, respectively). As variability in the surface velocity profile is likely to increase with flux gate width, uncertainties in the horizontally averaged velocities through the remaining seven flux gates were estimated using a regression (r
2 = 0.76) of the uncertainty in the horizontally averaged velocity against flux gate width for the four flux gates for which data were available (Table 5).
due to the choice of n was taken as the difference between estimates derived assuming n = 2.5 and 3.5 for a given flux gate. Uncertainty in the horizontally averaged velocity (σ
H[u
G] (m a−1)) is a function of how well two stakes in a flux gate represent the ‘true’ horizontal surface velocity profile perpendicular to the gate. To quantify this uncertainty, across-gate InSAR velocity profiles (Reference Burgess, Sharp, Mair, Dowdeswell and BenhamBurgess and others, 2005; Fig. 5) were linearly detrended and compared with the two-point velocity profiles derived from stakes. The standard error of the differences between the detrended InSAR profile and the two-point profile was taken to represent the uncertainty in the horizontally averaged velocity across each flux gate (σ
H[u
G]; Table 5). The standard errors are relatively low for gates that do not contain threads of fast-flowing ice (e.g. 1.6 m a−1 for gate 1), but much higher for those flux gates within which fast flow does occur (e.g. 6.6 and 13.3 m a−1 for flux gates 10 and 6, respectively). As variability in the surface velocity profile is likely to increase with flux gate width, uncertainties in the horizontally averaged velocities through the remaining seven flux gates were estimated using a regression (r
2 = 0.76) of the uncertainty in the horizontally averaged velocity against flux gate width for the four flux gates for which data were available (Table 5).
Table 5. The in situ-derived uncertainty in the horizontally averaged velocity (σ
H[u
G]), uncertainty in the vertically averaged velocity
![]() and total uncertainty in the width- and depth-averaged velocity
and total uncertainty in the width- and depth-averaged velocity
![]() for the 11 drainage basins
for the 11 drainage basins
Assuming that the errors in both the horizontally and vertically averaged velocities are independent and random, the total error in the width- and depth-averaged velocity through a given flux gate
![]() can be estimated as the quadratic sum of the fractional uncertainties in the two terms (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998):
can be estimated as the quadratic sum of the fractional uncertainties in the two terms (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998):
Likewise, assuming that the errors in each term used to compute the specific outflow are independent and random, the error in the mean annual change in surface elevation due to specific outflow from a given drainage basin (σ[dh O/dt] (m w.e.a−1); Table 3) can be estimated as (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998):
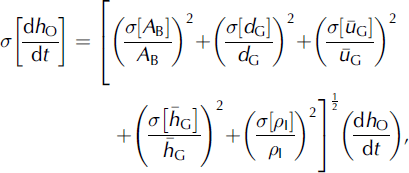
where σ[A
B] is the uncertainty in drainage basin area, assessed as 5% of A
B through repeat flowline traces, σ [d
G] is the GPS position measurement error at each stake,
![]() is calculated according to Equation (A1) for a given flux gate,
is calculated according to Equation (A1) for a given flux gate,
![]() is an assumed ice-thickness error of ±10 m (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004) and σ[ρ
I] is an assumed ice-density uncertainty of ±50 kg m−3,.
is an assumed ice-thickness error of ±10 m (Reference Dowdeswell, Benham, Gorman, Burgess and SharpDowdeswell and others, 2004) and σ[ρ
I] is an assumed ice-density uncertainty of ±50 kg m−3,.
Two sources of uncertainty affect the computation of the rate of surface-elevation change due to net accumulation in a given basin: (1) the uncertainty associated with the calculation of the mean annual net accumulation rate at each ice-core site, and (2) the uncertainty introduced by the use of MLR to predict the variation in net annual accumulation rates across the high-elevation region. The uncertainty in the mean annual net accumulation rate (σ[a c] (m w.e. a−1)) is assumed to be the quotient of the uncertainty in the water equivalent depth of the 1963 137Cs horizon (±0.1 m w.e.) over 40 years (±0.0025 m w.e.a−1). As the differences between observed and predicted net accumulation rates at the 13 core sites appear to be randomly distributed across the high-elevation region (Table 2), the uncertainty in the use of MLR to interpolate net accumulation rates (σ[a m] (m w.e.a−1)) was taken as the standard error of the MLR regression estimate (0.023 m w.e. a−1). The uncertainty in the mean annual change in surface elevation due to net accumulation (σ[dh A/dt] (m w.e.a−1); Table 3) was estimated as 0.023 m w.e. a−1 for all basins, according to (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998):
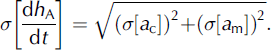
Assuming that the errors in both of the terms used to arrive at the calculated rate of thickness change are independent and random, the error in the mean annual change in surface elevation in a given drainage basin (σ[dh/dt] (m w.e.a−1); Table 3) can therefore be estimated as the quadratic sum of the fractional uncertainties in the mean annual changes in surface elevation due to both specific outflow and net accumulation (Reference Thomas, Csathó, Gogineni, Jezek and KuivinenThomas and others, 1998):