The Geometry of Water Veins and Nodes in Polycrystalline Ice

Abstract

Water in polycrystalline ice at its melting point forms a system of veins at the three-grain junctions. The veins join together at nodes, which are the four-grain junctions. The shape of a node, a tetrahedron with non-spherical faces and open corners, is determined completely by the dihedral angle for water in contact with a grain boundary. Using the observed value for this angle, namely 33.6°, the paper computes the tetrahedral shape. This is a surface-tension problem with initially unknown boundaries. The result shows that the ratio of vein volume to node volume is R = 0.072 l/d, where l is the average length of a vein between two nodes, and d is the vein diameter measured between edges. For example, in a specimen of ice grown from the melt in the laboratory R was 18.

1. Purpose of the Paper

Thermodynamical reasoning suggests (Nye and Frank, 1973) that polycrystalline ice at its melting point should contain water in the form of a three-dimensional network of veins. The veins lie along the lines where three ice grains meet (Fig. 1). At the points where four grains meet, the water veins come together in fours to form junctions called nodes. The main purpose of this paper is to compute from surface-energy considerations the detailed shape of a node. One can then deduce the relative volumes of water in the veins and in the nodes. Our conclusions on this topic appear at the end of section 4. Section 5 describes the details of the computation.

Fig. 1. The vein–node system. (Modified from Smith, 1948; not to scale.)

2. The Vein System and its Significance

The vein structure predicted by theory can be readily observed with a low-power magnifier, or even with the naked eye, in ice grown from the melt in the laboratory. It has also been observed and carefully studied in temperate glacier ice (Raymond and Harrison, 1975). In both cases, some water is also found at other locations within the grain structure, for example, as lenses at the grain boundaries (Nye and Mae, 1972), and Raymond and Harrison observed a few three-grain junctions without veins. Air and water-vapour bubbles are also seen.

There are several reasons why the vein structure is worthy of study. The first concerns the absolute scale of temperature. The triple-point temperature of water is the fixed point chosen to establish the size of the degree, and standard triple-point cells use polycrystalline ice (e.g. McAlIen, 1982). Therefore, the effect of the high curvature of the vein walls in lowering the equilibrium temperature is one of the potential variables that needs to be considered in achieving reproducibility. Another is the fact that impurities are likely to be preferentially concentrated in the veins and nodes, where they will have a disproportionate effect in lowering the equilibrium temperature.

In glaciers, a connected vein system can make the ice permeable to water on a microscopic scale, and a continuum theory of moisture transport can be based on this mechanism (Fowler, 1984). How efficient the mechanism is depends on the size of the veins and on the extent to which they may be mechanically blocked by air bubbles or strain (Lliboutry, 1971, 1976; Raymond and Harrison, 1975; Hantz and Lliboutry, 1983), or effectively sealed by thermal effects arising from bubbles and impurities (Raymond, 1976). The permeability of the basal ice in a glacier may have an influence on the basal sliding process by providing an additional path for the movement of water involved in regelation (Robin, 1976; Lliboutry, 1986). When fresh-water lake ice melts, the veins may enlarge to macroscopic channels and allow vertical movement of water (Browman, 1974). Likewise, the ice layers in a snow-pack become permeable to water as it reaches the melting temperature by enlargement of the veins, and the permeability effectively disappears if the prevailing temperature should drop, thus reducing their size (Langham, 1974).

Water, both in veins and in other locations, may also affect the creep rate of polycrystalline ice (Duval, 1977). Similarly, the steady deformation taking place in a glacier may redistribute the water between the veins and the grain boundaries, driving the system away from thermodynamic equilibrium (Nye and Mae, 1972); from this point of view, undeforming ice in the laboratory may not be altogether representative of glacier ice.

In glaciers the veins play another role by being about a thousand times richer in impurities than the grains themselves, and they thereby have a correspondingly important effect on the melting point. However, because of their relatively small volume in coarse-grained ice, the impurities they carry may be only about 1% of the total. In fine-grained ice this can increase to about 40% (Harrison and Raymond, 1976). As grain growth and recrystallization occur, gas inclusions or other impurities are transferred away from the grain interiors (Berner and others, 1977; Glen and others, 1977). One envisages a two-stage process; first, an impurity is swept up by a moving grain boundary, and then the grain boundary itself is swept by a moving vein. By this scavenging mechanism the veins would be expected progressively to purify the ice.

Liquid veins may exist even in polar ice. For example, in Antarctic ice, subsquently cooled to −160°C, the scanning electron microscope gives evidence that sulphuric acid is preferentially concentrated at the three-grain junctions (Mulvaney and others, 1988; Wolff and others, 1988), which suggests that in nature the junctions would contain liquid in spite of the low Antarctic temperatures. Indeed, Wolff and Paren (1984) attribute the d.c. conductivity of polar ice essentially to conduction along such liquid veins.

3. The General Geometry of the Vein System

The shape of the cross-section of a vein and the shape of a node are both dictated by surface energy, specifically by the ratio of the surface energy of an ice—water interface to that of a grain boundary (Nye and Frank, 1973). If we neglect any crystal anisotropy in these energies, water at a grain boundary has to penetrate it at a definite angle 2θ₀(Fig. 2), which by measurement (Walford and others, 1987) is 33.6 ± 0.7, with no observable influence of crystal orientation. Moreover, because the melting temperature of a curved ice—water interface depends on its total curvature (the sum of its two principal curvatures) and because in equilibrium the temperature must be uniform, it follows that the total curvature of the entire ice—water interface is uniform throughout the polycrystalline specimen. Thus, all the faces of both the veins and the nodes have the same total uniform curvature.

Fig. 2. Showing the dihedral angle 2θ₀ for water in contact with a grain boundary.

These are powerful constraints. They imply that, given the grain structure, and given the total volume of water contained in the veins and nodes, this channel system, in equilibrium, has an essential uniformity.

The veins must have three-fold symmetric cross-sections and the nodes must have the symmetry of a regular tetrahedron. Moreover, for thermodynamic equilibrium, each node must be identical to every other, and, similarly, the veins must all have identical cross-sections. Complete equilibrium would also require the veins to be straight, but in fact no three-dimensional grain structure exists that allows this (Figure 1 is misleading in this respect). Therefore, so long as the ice remains polycrystalline, the veins, and also the grain boundaries, must necessarily be curved. The tendency for the veins to become straight and for the grain boundaries to become flat entails a much slower process than the local re-adjustments that make the individual nodes and veins symmetric and uniform.

Thus, the structure consists of identical regular tetrahedra (the nodes) with concave non-spherical faces, and with the corners opening out into nearly straight veins. Asymptotically, the vein shape approaches a cylinder whose cross-section (Fig. 3) is an equilateral curvilinear triangle each of whose sides is an arc of a circle.

Fig. 3. Cross-section of a water vein at a triple-grain junction.

An essential point for this paper is that, once the dihedral angle 2θ₀ is fixed, an isolated node has a unique shape that is scale-free. In other words, changing the proportion of water changes the size of a node but not its shape. This means that the shape of an isolated node may be computed once and for all; there are no free parameters. Joining the nodes together results, as we have noted, in the veins becoming curved, but, because the veins approach their asymptotic form in such a short distance, the shape of an individual node is hardly affected either by vein curvature or by the presence of neighbours at a finite distance. The computation described in this paper finds the shape of an isolated node when 2θ₀ = 33.6°.

An answer can then be given to the question: what proportion of the water in the vein–node system resides in the veins rather than in the nodes? And to the related question: if some extra water is provided in the system by melting, how much of it will appear in the veins and how much in the nodes? To see that the questions are not trivial, consider for a moment the hypothetical case when 2θ₀ = 60°. Then, as discussed in Nye and Frank (1973), the nodes become spherical-faced concave tetrahedra. The tetrahedral edges, which are then arcs of circles, meet tangentially at the corners and the veins close up completely. So, if 2θ₀ were 60°, the proportion of water in the veins would be zero, and any new melt water would go exclusively into the nodes. On the other hand, observations suggest that, with 2θ₀ taking its measured value of 33.6°, a substantial proportion of the water in the vein—node system is in the veins. One of our purposes is to establish by computation what proportion this is.

Because the nodes shade continuously into the veins, the distinction between the two is not a sharp one. However, as they leave the nodes the veins approach their asymptotic form so fast that the potential difficulty of defining precisely where one stops and the other begins in fact makes little quantitative difference.

Our discussion has been about pure polycrystalline ice. In practice, as was mentioned in section 2, the impurities in a polycrystalline specimen formed from the melt are preferentially concentrated in the veins and nodes, where they will lower the melting point. This will be a uniform effect throughout the vein–node system, because the concentration of impurities in the liquid will tend to become uniform. Therefore, the overall effect will be simply to lower the melting point; for a given volume of liquid, the geometry of the system will not be affected. We do not assume that all the water in a polycrystalline specimen resides in the vein–node system. The question we are concerned with is how the water which is in this system is distributed between the veins and the nodes.

4. The Detailed Geometry

Consider first the asymptotic cross-section of a vein (Fig. 3). The distance d between the corners of the triangle is related to the radius of its sides r_v by

(1)

The area of cross-section can be expressed in terms of r_v as αr² _v, where

(2)

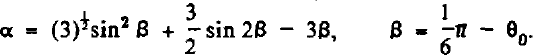
It is useful to define an equivalent radius r₀ by

(3)

Thus, a circle of radius r₀ would have the same area as the vein cross-section.

Let us suppose that, on average, each section of vein joining two nodes has length l, and suppose the total number of nodes is л. By associating each node with four veins each of length we see that the total length of vein is 2nl. Hence the total vein volume is . We make an arbitrary decision that a vein ceases to be called a vein when its cross-section has flared out to a fraction 1 + ε of its asymptotic value. We shall find, as already mentioned, that the exact value taken for ε (0.1 or 0.05, for example) makes little difference to the final result. With this definition, since the shape of the node is independent of scale, we can write its volume as , where μ is a dimensionless computable number. The total node volume is , and the ratio of vein volume to node volume is then Thus, if we can estimate l/r ₀, the ratio of vein length to radius, the proportion of water in the veins depends only on μ, and this is the number we have to compute. Note that, for given l, the narrower are the veins the greater is the proportion of water they contain.

In the computations (Fig. 3) is taken as unit length, and the node volume computed in these units is denoted by V _n. Thus

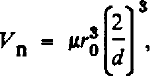
and by combining this with Equations (1) and (3) we find

where α and β are given by Equations (2). Inserting the measured value 2θ₀ = 33.6° yields α = 0.06612 and

In computing V_n the only adjustable parameter (apart from the mesh size) is ε, and the results are shown in Table II. The computed value of K_n is found to be 70, with the precise value depending on the choice of ε, and hence we conclude that

The ratio of vein volume to node volume is then

As a measure of vein size, the observable quantity is the edge separation d (Fig. 3) rather than r ₀, and in terms of d we find

As an example, in a specimen of ice grown from the melt in the laboratory and allowed to heat up to the melting point, d was measured as 20 μm and I was estimated as 5 mm, yielding the ratio R = 18. For the water to be equally distributed between the veins and the nodes, melting would have to enlarge the veins to a width d = 360 μm. This would be extreme; normally there will be much more water in the veins than in the nodes.

The question was also asked: if a small amount of extra water is made by melting, what proportion of it will appear in the veins? Since while , it follows that

Thus, in the above example, where R =18, 12 times as much new water would appear in the veins as would appear in the nodes.

These are our main conclusions of physical interest. The remainder of the paper describes how the detailed node shape and the results of Table II were computed.

5. Computational Method

The physical conditions to be obeyed by the ice-water interface are first, that the sum of its two principal curvatures at each point is a constant, and second, that at the edges the two faces should meet at the constant angle 2θ₀. The problem is equivalent to the following one in surface tension (Fig. 4). Consider three planes* А, В, C whose normals are symmetrically arranged about an axis OZ and which make equal angles of cos⁻¹(2/3)½ = 35.26° with it. Into the corner thus formed (rather flatter than the corner of a cube) place a drop of liquid and require that the contact angle between liquid and solid (that is, any one of the planes) be θ₀. The liquid surface so formed has the same shape as one face of our node. Thus, the three contact lines, L say, of the liquid drop are the edges of the node, and repeating this surface four times gives the complete shape of the node. This equivalent version of the problem is perhaps easier to vizualize and we shall use it in what follows.

Fig. 4. A re-entrant corner formed by three planes A,B,C, whose normals make equal angles of 35.26 with the normal to the diagram. A drop of liquid having contact angle θ₀ lies in the corner. The contact lines are labelled L. The liquid surface has the same shape as one face of a node. The figure is drawn to scale, projected parallel to OZ.

The main computational problem is that the shape of the contact lines L (or node edges) is not known in advance (although of course they have to lie in the relevant planes). The method used is to start with a trial shape for this line and to find the corresponding surface of constant total curvature (a surface-tension problem) by a finite-difference successive approximation procedure. This yields a contact angle, θ say, between liquid surface and plane, that varies along the contact line. The line is then adjusted normal to itself by an amount k(θ − θ₀), k being a selected constant, to a new position, and the new surface of constant curvature found. If the value of k has been well judged, the new, but still non-uniform, contact angle will now be closer to the required uniform value θ₀. The process is repeated until no further improvement takes place.

A potential problem with this procedure is that to solve the surface-tension problem even with a given boundary L requires a knowledge of the constant total curvature, K say. If one starts by fixing the asymptotes of L, which are the asymptotic vein edges, d, the distance between them, is fixed and therefore also r _v by Equation (1). Then, because one principal curvature at infinity is zero, К = 1/r_v and so K is determined. But this could be awkward numerically because L will actually be computed only over a finite length rather than to infinity. However, although this might have been troublesome in theory, L turned out to approach its asymptote so' fast that in practice there was no difficulty.

Because of the symmetry, it is sufficient to compute only a representative one-sixth of each node face; repeating this 24 times gives the complete figure. Figure 5 shows this representative piece schematically viewed along a three-fold axis of symmetry OZ, the origin O being taken at the centre of the node. The axes OX, OY, perpendicular to OZ, lie in the plane of the diagram, OY being the projection of the vein axis, which runs at an angle to OZ of cos⁻¹(1/3) = 70.53°. The auxiliary axis Ox is also in the plane of the diagram and at 30° to OX. The edge L of the node lies in a plane (B in Figure 4) whose normal makes an angle with OZ and is coplanar with OZ and Ox. The line marked L′ is the projection of this edge L on to the plane of the diagram. The point A is taken far enough up the vein to be effectively on the asymptote, as we have just explained, and is fixed throughout. The field to be computed is h X,Y), the height of the interface above the plane Z = 0, over the region bounded by OCAPO.

Fig. 5. Coordinate system and grid used in the computation.

Differential equation. The condition is that

where R ₁ and R ₂ are the two principal radii of curvature of the surface Z = h (X, Y) at each point. Then, using a standard formula (Bronshtein and Semendyayev, 1971, p. 311), we find

(4)

Where p = h _X, q = h _Y, s = h _XY, t = h _YY

and

Subscripts denote derivatives and note that no small-angle approximation is used. The value of K is determined, as explained above, from the relation

using Equation (1), and we fix the overall scale by taking AC = 1.

Boundary conditions. On OC symmetry dictates that grad h (X,Y)is parallel to OY; thus h _X = 0. Similarly, on OP grad h(X,Y) is parallel to Ox; thus h _X,h _Y = (3)

.

On AC, provided it is taken at large enough Y, the surface is parallel to the vein axis, which provides the condition h _y = 1/2(2). On the node edge L, which we have to adjust, the surface meets the plane Z = (1/2(2) ((3) X + Y) and so on L′, its projection, the condition is h(X,Y) = (1/2(2) ) ((3) X + Y).

After h (X),Y) has been computed, we need to calculate on L' the angle θ between the surface Z = h (X,)Y) and the plane Z = (1/2(2))((3) X + Y) from the formula

(5)

Then L' is adjusted until θ = θ₀. As a first trial L' was taken as a straight line AA₁ (Fig. 5) and an arc of a circle A₁P parallel to OY at A₁ and perpendicular to Ox at P. AP was always a smooth curve passing between grid points.

Finite-difference scheme. The solution region was covered by a rectangular grid (Fig. 5) with proportions chosen to make Ox a line of grid points. The spacing parallel to OX was uniform with N₁ intervals in AC. The spacing along OY was made non-uniform, as follows, so as to reach far enough up the vein as economically as possible. OC was divided into N₃ sections. In the first section OC₁ there were N₂ intervals of equal length ΔУ, in the second section N₂ intervals of length 2ΔΥ, and so on, doubling the interval in each section to reach C.

To program the boundary conditions, the values of A obtained by extrapolation at exterior points (not shown in Figure 5) were used, taking care to avoid schemes that introduced instabilities. In the finite-difference approximation (Fig. 6) to the differential equation (4) centred differences were used for the first derivatives p,q. Then, since the value of A at the central point appears only in the second derivatives r and t, which occur linearly, we can readily solve for A at the central point in terms of A at the eight surrounding points.

Starting with a trial function h(X,Y) that fitted the required boundary height on AP, the values of h at interior mesh points were successively improved in this way. Convergence was made faster by using over-relaxation, the adjustment computed for A at the central point of Figure 6 being increased by a factor f, usually taken as 1.9. The solution, for a set position of AP, was regarded as achieved when the adjustment at all grid points had decreased to less than 10⁻⁵ (or 10⁻⁶ in some cases). Typically between 10 and 50 iterations over the grid were sufficient for this.

Fig. 6. Illustrating the finite-difference scheme used in the computation.

The contact angle θ was then computed from Equation (5) at mesh intervals along AP and compared with the target value θ₀. The X coordinates of AP were increased by k(θ – θ ₀), k being adjustable and typically 1 or 0.7. Then AP was slightly smoothed before finding the new solution for h(X,Y) and repeating the procedure. The process was stopped when there was no further decrease in | θ - θ₀ |; this needed 30–50 iterations.

Table I shows results for successively finer grid spacings specified by N₁ and N₂. With the finest grid the maximum discrepancy in contact angle | θ – θ| ₀1 was 0.003 radian = 0.2°, which is less than the reported error (0.7°) in the measurement of θ₀ itself. Table I contains values of h at the origin, which is the radius of a sphere inscribed

Table. I. Computed Values Of л At O And Of OP (AC = 1)

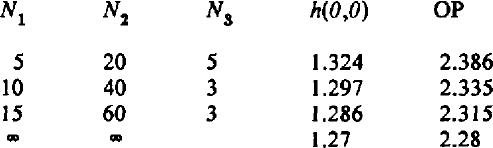
within the node, and of the length OP measured in the XY plane. These values vary linearly with the interval, and therefore we extrapolate to zero interval to obtain the final result shown in the last line.

In the same way, the whole solution for h(X,Y) was extrapolated to zero interval and then the various volumes shown in Table II were computed (these refer to the whole node, not just the representative piece). The volume of the node depends, as pointed out in section 4, on making an arbitrary choice of where the node ends and a vein begins. If we choose this point as being where a vein has narrowed to within 12% of its asymptotic area (line 1 of Table II), the node volume is 67.4. The volume is not sensitive to the exact criterion used: if the difference from the asymptotic area is anywhere between 12 and 5%, the volume is 70 ± 3.

Table. 2. Volume Of A Node

1 + ε = ratio of cross-section of vein where it joins the node to its asymptotic cross-section.

V _n = volume of node.

V_i = volume of sphere that touches node faces.

V ₀ = volume of sphere that touches node edges.

The unit of length is ½ d = AC.

ε V _n V _i•V ₀

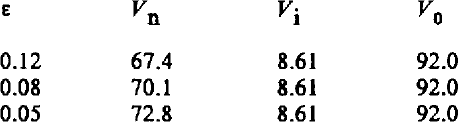
The final value of V _n is 70 :± 3 within the range 0.05 > ε > 0.12.

Table II also shows the volume of the sphere inscribed within the node, and also of a sphere that touches each of the six node edges L at its mid-point (the latter has a radius (3/2) times OP).

Operating on the coordinates of the computed portion of the node surface, first with two mirror planes to produce a complete face, and then with diad axes, generates the complete node as drawn in perspective in Figure 7a and b.

Fig. 7. Perspective views of a node, to scale, (a) is viewed from a distance of 16 units and (b) from a distance of 20 units. (The curves outlining the cross-sections of the veins lie accurately in the vein surfaces, but in planes parallel to OZ and its repetitions. Thus, they differ very slightly from plane cross-sections.)

Acknowledgement

Laboratory work on ice veins was supported by a grant from the U.K. Natural Environment Research Council.