Introduction
The prediction of the velocity at which a floating fragment of ice will be swept under the leading edge of a down-stream cover is one of the most basic problems in understanding the mechanics of a broken cover of river ice. The solution of this problem has application in determining the initial conditions and evolution of ice jams, in the design of ice booms and ice retention facilities on rivers, in the design of channels to attain a stable ice cover, and in a number of other topics where the accumulation of floating materials under the influence of a flow velocity is important. In keeping with its intrinsic importance, this problem has attracted the attention of a number of investigators over the past few decades. It is surprising, therefore, that the problem has not been adequately solved. Investigators continue to report data in terms of a Froude number based on water depth while obscuring the rather vital dependence on ice thickness. In this paper, dimensional analysis is applied to the problem. The experimental results of a recent comprehensive laboratory investigation (Reference Uzuner and KennedyUzuner and Kennedy, 1972) are examined in the light of the analysis, and the two are shown to be consistent. Specifically the critical velocity is found to be a simple function involving the Froude number based on block thickness and the ratio of block thickness to flow depth, and to be but little affected by the ratio of thickness to length or the Froude number based on depth.
Summary of previous work
The work previous to 1968 has been summarized by Reference BolsengaBolsenga (1968). Early attempts to establish criteria were expressed in terms of a velocity above which a cover will not progress up-stream. Reference KivisildKivisild (1959) apparently introduced the Froude concept and concluded that the limiting value for up-stream progression was given by

wherein V c is the critical velocity measured up-stream of the block, t is the fragment thickness, and ρ and ρ′ are the densities of the fluid and the fragment respectively. Perhaps under the influence of Kivisild’s previous suggestion of an F H criterion, they chose to present their experimental results in the form

thus reinforcing the previous suggestion of an F H criterion. The coefficient K in Equation (2) was included in cognizance of the fact that most floes submerge by under-turning, generally at a lower velocity than predicted by Equation (2) with K = 1.0. Since then numerous papers have presented ice-jam data by giving only the value of the associated F H and mentioning t only in passing, if at all (e.g. Reference MichelMichel, 1971, in press; Reference OudshoornOudshoorn, [1971]).
Recently Uzuner (unpublished) and Reference Uzuner and KennedyUzuner and Kennedy (1972) analyzed the problem, again assuming a “no-spill” condition but considering under-turning to be the governing mode of instability. Uzuner and Kennedy also presented the results of their laboratory experiments in terms of F H and t/H with the added parameters of t/L and C m, the latter an empirically determined “moment coefficient” which is a function of t/L and ρ′/ρ. Their experimental results covered a range of ρ′/ρ from 0.37 to 0.89 and t/L from 0.096 to 0.773.
As will be shown below, a dimensional analysis suggests that the most significant parameter is a Froude number based on block thickness rather than flow depth. Further, a simplified moment analysis yields results in good agreement with experimental data and without recourse to an empirical parameter.
Dimensional analysis
The pertinent variables in the problem are the velocity V c, the block thickness t, the block length L, the flow depth H, the weight per unit volume of the fluid and the block, γ = ρg and γ′ = ρ′g respectively, and the density of the fluid ρ. The weight per unit volume of the air is taken as zero relative to γ and is thus not explicitly included in the analysis. Considering first the case of large depths, physical reasoning leads us to expect that instability occurs when the pressure forces due to the velocity exceed the buoyant forces due to the weight difference between the block and the fluid. Accordingly, a ratio of the two forces is expected to be the most significant parameter. The pressure forces may be taken to be proportional to ρV c 2 multiplied by an area chosen to be the length of the block L times its width B. The buoyant force at full submergence is (γ—γ′)tLB. The ratio of the two forces is

which may be put into the usual form of a densimetric Froude number by substituting γ = ρg and γ′ = ρ′g and taking the square root to yield
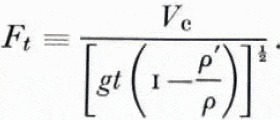
This Froude number does not include the block length or the flow depth. To complete the dimensional analysis we expect F t to be a function of parameters incorporating these dimensions in the form

where f denotes functional dependence.
Examination of Pariset and Hausser’s criterion (as given by Equation (1)) suggests that t/H is more important than t/L. Accordingly, the data of Reference Uzuner and KennedyUzuner and Kennedy (1972) have been plotted in Figures l, 2 and 3 with F t as the ordinate and t/H as the abscissa, with different symbols assigned to various combinations of t/L and ρ/ρ′. The choice of coordinates has the additional advantage of allowing ready determination of the critical velocity for conditions when F H is obviously illogical as is the case for special flow configurations or large depths. The data are seen to fall in a narrow band generally below the criterion given by Pariset and Hausser in Equation (1). Before leaving the results of the dimensional analysis it is worth while to point out that the ratio t/L is not entirely irrelevant. Close examination of the Figures reveals a weak trend of decreasing stability (lower critical velocity) with increasing t/L. This trend is particularly evident in Figure 3 where the data for t/L = 0.096 lies generally above the other data sets. This behavior is not as marked for the same value of t/L at lesser values of ρ′/ρ; see Figures 1 and 2.

Fig. 1. Ft versus t/H (data of Reference Uzuner and KennedyUzuner and Kennedy (1972)).
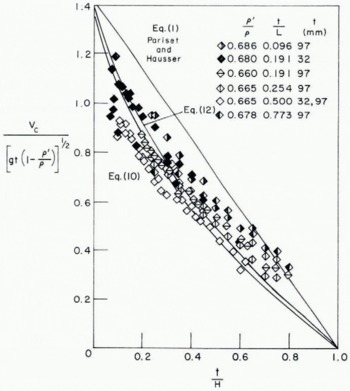
Fig. 2. Ft versus t/H (data of Reference Uzuner and KennedyUzuner and Kennedy (1972)).
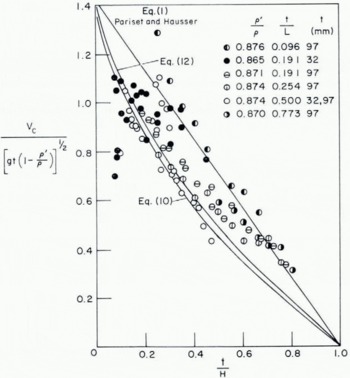
Fig. 3. Ft versus t/H (data of Reference Uzuner and KennedyUzuner and Kennedy (1972)).
Simplified analysis
While the analysis presented below is not as detailed as that of Uzuner and Kennedy, it yields simple analytical results which will be shown to be in good agreement with the experimental data. Further, its simplicity enables the physical meaning of the various assumptions used to be explicitly shown, particularly the effect of depth on the critical velocity. It is shown that under-turning occurs at a lower critical velocity than vertical submergence.
A definition sketch is presented in Figure 4. The block is assumed to rotate about its down-stream end and to be submerged such that the bottom is a distance t 1 below the water surface. The velocity beneath the block (of unit width) is assumed to be uniform and denoted by V u. Taking moments about point A and assuming equilibrium results in

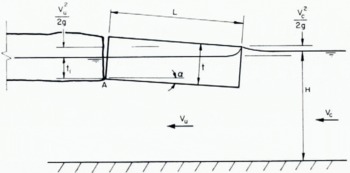
Fig. 4. Definition Sketch.
The first term in Equation (5) represents the under-turning moment due to the weight of the block, the second term the under-turning moment due to the pressure reduction associated with the Bernoulli effect, the third term the restoring moment due to the weight of the water displaced by that volume of the block described by t 1 L, and the last term the restoring moment due to the weight of the water displaced by that submerged portion of the block triangular in section with height L sin ⍺. It is convenient to divide Equation (5) by ρgtL 2/2 resulting in

We now introduce the same no-spill condition used by others. Specifically we assume incipient instability occurs when the top up-stream edge of the block submerges, that is, when

Substituting for L sin α in Equation (5a) from Equation (6) results in

An assumption about t 1 must now be introduced and there are a number of reasonable choices. First, it is assumed that t 1 = tρ′/ρ, i.e. the hydrostatic equilibrium depth. For this case Equation (7) leads to

Introduction of continuity by the relationship
leads to

Alternatively the depth t 1 may be taken as the depth at which the block arrives from up-stream, which is

Again introducing continuity, Equations (7) and (11) result in

Relationships (10), (12) and (1) are plotted in Figures 1, 2 and 3. It is clear from an examination of the Figures that Pariset and Hausser’s criterion overestimates the critical velocity particularly since Uzuner and Kennedy reported surface velocities about 14% higher than the mean velocity V c. In view of this uncertainty it is difficult to choose between Equations (10) and (12) as best representing a stability criterion. The significance of t/H is clearly due to the effect of the block constricting the flow cross-section, thus increasing the velocity in accordance with simple continuity.
The analysis presented above could, of course, be made more detailed by consideration of other effects acting on the block such as the pressure against the up-stream face. It seems more logical, however, to replace the heuristic assumption of the no-spill condition by a formal stability criterion; it is expected that such efforts would lead to an explanation for the observation that blocks of either very small or very large t/L ratio submerge vertically rather than under-turning.
We would have liked to present field data instead of laboratory data. Unfortunately, because of the preoccupation with F H , ice thickness and surface velocity have seldom been reported. It is hoped that in the future these will be given proper attention.
Acknowledgements
The writer gratefully acknowledges helpful discussions with Samuel Colbeck and Wilford Weeks of the U.S. Army Cold Regions Research and Engineering Laboratory. This work was supported by DA Project No. 4A062103A894, Engineering in Cold Environments.






