Flow dynamics of tidewater glaciers: a numerical modelling approach

Abstract

The dynamics of grounded tidewater glaciers is investigated with a time-dependent numerical flow model, which solves the full equations for the stress and velocity fields and includes a water-pressure-dependent sliding law. The calving criterion implemented in the model shifts the calving front at each time-step to the position where the frontal ice thickness exceeds flotation height by a prescribed value. With this model, the linear relation between calving rate and water depth proposed on empirical grounds is qualitatively reproduced for the situation of a slowly retreating or advancing terminus, but not for situations of rapid changes. Length changes of tidewater glaciers, i.e. especially rapid changes, are dominantly controlled by the bed topography and are to a minor degree a direct reaction to a mass-balance change. Thus, accurate information on the near-terminus bed topography is required for reliable prediction of the terminus changes due to climate changes. The results also confirm the suggested cycles of slow advance and rapid retreat through a basal depression. Rapid changes in terminus positions preferably occur in places where the bed slopes upwards in the ice-flow direction.

1. Introduction

This study investigates tidewater glaciers, which are defined as glaciers that end in the sea with a grounded ice cliff from which icebergs are discharged. The present paper approaches the dynamics of tidewater glaciers with a time-dependent numerical flow model. The model solves the full equations for the stress and velocity fields, including a water-pressure- dependent sliding law. A calving criterion is implemented which removes at each time-step the part of the glacier terminus that is thinning below a critical height above buoyancy. Thus, the calving rate, which is defined as the ice velocity at the terminus minus the rate of change in the terminus position, is an output quantity of the model. This represents important progress in the investigation of the evolution of tidewater glaciers by means of a numerical glacier flow model.

The model is applied to a geometry characteristic for tidewater glaciers with a basal depression in the terminus region. Model calculations performed for two mass-balance scenarios have led to an advancing and a retreating situation mainly over the basal depression. With these model experiments it is intended to demonstrate how the changes of the calving front are affected by the physical processes considered and their feedback mechanisms. The qualitatively described concepts and processes suggested for tidewater glaciers on the basis of observations (Meier and Post, 1987; Van der Veen, 1996) will also be examined.

1.1. Motivation

The dynamical behaviour of tidewater glaciers is important because of their reaction to climate change, but is still poorly understood (Meier, 1994; Van der Veen, 1997a). Observations of several glaciers, such as Columbia Glacier, Alaska, U.S.A. (Meier and Post, 1987), Glaciar Upsala, Patagonia (Warren and others, 1995b), Glaciar San Rafael, Chile (Warren and others, 1995a), and records of past glacial expansion (Powell, 1991) show that tidewater glaciers have a great potential for dramatic retreats of the terminus position. For example, Columbia Glacier retreated at a rate of about 0.7 km a⁻¹ from 1985 to 1991 (Krimmel, 1992). Iceberg calving is a very efficient ablation mechanism and permits a much larger rate of mass loss than surface melting (Van der Veen, 1996). A generally high calving activity can strongly increase the fresh-water input into the ocean in the form of icebergs and may have a strong impact on the environment. For example, during the rapid retreat of Columbia Glacier, drifting icebergs posed a serious threat to oil tankers (Dickson, 1978). The additional fresh water may also affect the marine ecosystem in the surrounding sea. During the last glaciation, large quantities of icebergs were discharged by the Laurentide ice sheet six times. They were recorded in a set of ice-rafted debris deposited in sediment layers in the North Atlantic (Heinrich, 1988). These so-called Heinrich events are connected with rapid climate variations in the North Atlantic region. It was speculated (Broecker, 1994) that the additional fresh water from the discharged icebergs disrupted the deep-water formation, thereby switching the thermohaline ocean circulation between glacial and interglacial modes (Dansgaard–Oeschger events). Thus, studying the present tidewater glaciers may provide a better understanding of the past changes.

The rapid changes in the terminus position of Columbia Glacier during recent decades (Meier and Post, 1987) and of several Patagonian grounded calving glaciers (Warren, 1993; Naruse and others, 1997) are not directly related to climate. Meier and Post (1987) mentioned that longer periods of warm climate may have triggered rapid retreats by glacier thinning in the terminus region. Clarke (1987) suggested that tidewater glaciers inherently have an unstable response to a long-term mass-balance deficit. In view of the potential for rapid changes of tidewater glaciers as a response to climate changes, improved knowledge of the dynamics is essential.

1.2. Current knowledge on tidewater glaciers

Several processes that influence the dynamics of tidewater glaciers have been identified, and these may be important to control the position of the terminus. Empirical studies showed that the calving rate increases linearly with water depth at the terminus (Brown and others, 1982). It has also been recognized that bed topography plays an important role in the control of changes in the terminus position (Meier and Post, 1987). Tidewater glaciers typically end at a submarine frontal moraine. When the terminus starts to retreat into deeper water, the calving activity increases and results in a dramatic retreat, which has been observed for many tidewater glaciers (Van der Veen, 1997a; Venteris, 1999). Meier and Post (1987) suggested that tidewater glaciers undergo a cycle of slow advance (on the order of a few hundred to a thousand years) and rapid retreat (decades to a century) through a depression in the basal topography.

Basal sliding is known to be an important factor in controlling the dynamics of tidewater glaciers (Meier and Post, 1987; Van der Veen, 1996) and is related to basal water pressure (Iken, 1981; Bindschadler, 1983). Observations at Columbia Glacier showed that the sliding velocity at the terminus increases with increasing calving rate, thus reducing the rate of position change (Van der Veen, 1996). Data from many tidewater glaciers show that there is a good correlation between calving rate and ice speed at the terminus (Van der Veen, 1996; Jania and Kaczmarska, 1997). For glaciers in steady state this correlation is a direct consequence of the definition of the calving rate, but for rapidly changing glaciers there is no such evidence (Van der Veen, 1996). Furthermore, it is still not clear whether increased calving leads to increased sliding or vice versa.

Back pressure from the terminal moraine may also affect the ice flow (Van der Veen, 1997a; Fischer and Powell, 1998). When the terminus retreats and loses contact with the frontal moraine, the back stress is expected to decrease and the velocity at the terminus will increase due to enhanced horizontal stretching (Meier and Post, 1987), and the rate of retreat will be reduced.

On long time-scales (hundreds of years) sedimentation processes and the formation of a terminal moraine become important (Powell, 1991; Hunter and others, 1996; Fischer and Powell, 1998). The filling of the basal depression in front of the glacier and the growing terminal push moraine reduce the water depth and therefore the calving activity. Hence, an advance of the glacier through a basal depression is facilitated, as already observed at Taku Glacier, Alaska (Motyka, 1997) , and Hubbard Glacier, Alaska (Mayo, 1989).

Which processes initiate a retreat or advance of a calving glacier is still an open question. Even the comprehensive dataset of rapidly retreating Columbia Glacier does not allow the identification of the mechanisms that cause and control a terminus retreat. Two different conceptions have been proposed.

Meier (1994, 1997) suggested that calving is the driving mechanism for a retreat. His conception is based on the proportionality of the calving rate to the water depth (Brown and others, 1982). Meier claims that increased calving rates lead to additional horizontal stretching at the terminus as the increased cliff height causes higher unbalanced lithostatic stresses. Increased horizontal stretching will then lead to a thinning of the glacier terminus and the effective pressure will decrease, followed by an increase in basal sliding and additional horizontal stretching. If the calving rate is related to the extension rate, the calving activity will increase and enhance the retreat. On the other hand, the increase of sliding due to glacier thinning will reduce the retreat (Meier and Post, 1987).

A different concept is proposed by Van der Veen (1996, 1997b). He maintains that if thinning takes place at the terminus due to increased flow velocity and horizontal stretching, the calving activity and therefore the rate of retreat will increase. Observations at Columbia Glacier (Meier and Post, 1987; Van der Veen, 1996) and rapidly retreating grounded calving glaciers in Patagonia (Venteris, 1999) showed that the part of the terminus which is thinning below a critical height above flotation breaks off due to buoyancy. In this interpretation, the retreat is initiated and maintained by thinning and stretching of the glacier.

Meier’s and Van der Veen’s opposing concepts show that the involved physical processes lead to complex feedback mechanisms. We therefore propose to approach the problem by means of a numerical glacier model, which allows coupling of the relevant processes concerning the dynamics of tidewater glaciers.

1.3. Previous modelling work

At the beginning of the rapid retreat of Columbia Glacier in the early 1980s several numerical models were developed in order to predict the future retreat of this tidewater glacier. Rasmussen and Meier (1982) used a one-dimensional model based on mass conservation. In this model the calving rate was specified by a linear function of the water depth at the terminus. A drastic retreat that strongly depends on the parameters of the calving function was predicted.

Sikonia (1982) modelled the flow in a vertical section along the flowline. Basal sliding was simulated by using a thin soft layer at the glacier bed. The calving rate was related to ice thickness above buoyancy and to seasonal variations of fresh-water runoff. The modelled length change was extremely sensitive to the parameters used in the calving function. For small variations of these parameters the reaction of the glacier ranged between no retreat at all and a rapid retreat.

Bindschadler and Rasmussen (1983) developed a finite- difference model that calculated the ice flux for a finite number of cross-sections and updated the glacier geometry using the continuity equation. The ratio of the sliding velocity to the total surface velocity was determined from observed velocities and was assumed to be a constant for each point in space. Different parameterizations for the calving rate were used which related the calving rate linearly to water depth or front height. If flotation was reached at the terminus, the floating ice was removed. According to the model results, a rapid retreat was expected. Calculations could only be performed for a few hundred meters of retreat due to limitations in computing time. According to the results of all three models, a rapid retreat of Columbia Glacier was expected. Surprisingly, the observed glacier retreat was much slower than predicted, mainly because the flow velocities increased more than expected (Meier, 1994).

In a similar setting, the retreat of Unteraargletscher, Switzerland, ending in a planned new reservoir was estimated. Funk and Rothlisberger (1989) proposed and used an approach in which they estimated the mass flux and the empirical calving rate as a function of water depth. For a similar problem on Austdalsbreen, Norway, Hooke and others (1989) followed this approach, but also discussed the effect of a changing water level on basal sliding.

2. Governing Processes

A model of the dynamics of a tidewater glacier must incorporate realistic descriptions of calving and basal sliding, and must consider interactions between the calving process and the dynamics of the entire glacier (Van der Veen, 1997a).

2.1. Calving

The calving rate u _c is defined as the volume of ice that breaks off per unit time and per unit vertical area from the glacier terminus (Paterson, 1994, p. 376). It is equal to the ice velocity at the terminus, u _i, minus the rate of change in the terminus position L:

(1)

With this formulation, the ice lost by melting at the calving front is included in the calving rate. Most theoretical studies of calving were applied to floating glaciers and ice shelves (Reeh, 1968; Holdsworth, 1978). Hughes (1992) developed a theoretical model for calving of grounded glaciers based on the idea that bending shear is the controlling mechanism for calving. This theory cannot explain unambiguously the observations on tidewater glaciers and cannot be applied to tidewater glaciers close to flotation at the terminus (Van der Veen, 1996).

Several quantities, such as water depth, front height and ice velocity, show a close relationship to the calving rate. Based on data of 12 Alaskan tidewater glaciers, Brown and others (1982) proposed a proportionality between calving rate and water depth d at the terminus:

(2)

with a coefficient of 27.0 a⁻¹. Pelto and Warren (1991) proposed a similar, linear relationship with additional data from glaciers in Greenland and Svalbard. For glaciers calving into fresh water, a 15 times smaller slope coefficient β of the linear relationship between calving rate and water depth has been found (Funk and Röthlisberger, 1989). However, recent studies of the large Patagonian glaciers calving into lakes, such as Glaciar San Rafael (Warren and others, 1995a) and Glaciar Moreno (Rott and others, 1998), do not confirm a smaller slope coefficient β for fresh-water calving glaciers. The proposed relations are empirical and do not describe the mechanisms of calving. Van der Veen (1996) pointed out that the empirical linear relation in Equation (2) is based on data from glaciers which are in or close to steady state. The observed calving rates during the rapid retreat of Columbia Glacier and several other grounded calving glaciers (e.g. Hansbreen (Jania and Kaczmarska, 1997); Glaciar San Rafael (Warren and others, 1995a); Maud Glacier (Kirkbride and Warren, 1997)) are not consistent with the linear calving relation. A linear calving relation may not be valid during rapid changes of glacier termini (Meier and Post, 1987), as observed at Columbia Glacier. However, these empirical relations can be adopted as a working hypothesis, and a calving model should meet these relations.

Flotation model

Based on the observations at Columbia Glacier, an alternative treatment of calving is suggested in the flotation model (Van der Veen, 1996). During the rapid retreat of Columbia Glacier, the terminus appeared to retreat to a position where it approached flotation thickness (Meier and Post, 1987). In the flotation model, the terminus of the glacier retreats to the position where the ice thickness h exceeds the flotation height by an amount h _o (Van der Veen, 1996). The height at the terminus h _c is then given by

(3)

where ρ _w is the density of sea or fresh water (1030 or 1000 kg m⁻³) and ρ _i is the density of glacier ice. This implies that the part of the terminus where the ice thickness is below the critical thickness h _c calves off because the ice can no longer resist the buoyancy force. The final detachment is probably due to additional weakening of the ice by the formation of bottom crevasses when flotation is approached (Van der Veen, 1998). Applying this model to the rapid retreat of Columbia Glacier, Van der Veen (1996) found h _o = 50 m. The flotation model is consistent with the observed rapidly retreating calving glaciers in Patagonia, where a similar critical height above buoyancy was derived (Venteris, 1999). In the flotation model the calving mechanism does not need to be entirely understood, which favours its use in a numerical model in order to calculate the evolution of tidewater glaciers.

To date, the flotation model has only been tested with datasets of large fast-flowing tidewater glaciers (water depths of 150–300 m, flow velocities of 1000–6000 m a⁻¹). For smaller glaciers (water depths <150 m, flow velocities <200 m a⁻¹) the observed frontal cliff heights generally do not exceed 50 m, and the height above flotation is expected to be well below the 50 m suggested for Columbia Glacier. Therefore, we propose a modified flotation criterion where the fixed minimum height above flotation h _o in Equation (3) is replaced by a small fraction q of the flotation thickness at the terminus. The height at the terminus is then

(4)

For this modified flotation criterion, the terminus moves to the position where the ice thickness corresponds to . Choosing q = 0.15, the resulting is equal to the observed value of for Columbia Glacier.

Melt-induced calving model

For small and slowly flowing tidewater glaciers, parts, or all, of the terminus are generally far above the critical height , and the calving rates are small (<150 m a⁻¹). In this case, the observed calving rates cannot be described by means of the flotation model, and other processes are controlling the calving rate. For these slowly flowing tidewater glaciers, melting at the front may become important, although the average amount of ice lost by melting is small compared to the mass loss by calving (Powell, 1988). According to observations, melting is concentrated at the water-line (Fig. 1), due to wave erosion. Observations from Glaciar San Rafael (Warren and others, 1995a) and Le Conte Glacier, Alaska (personal communication from K. A. Echelmeyer, 2001), indicate that excessive melting may also take place below the water-line. As for the deterioration of icebergs, melting at the water-line was found to be one order of magnitude higher than subaqueous melting forced by buoyancy convection (El-Tahan and others, 1987). Thus, the vertical ice front is undercut by melting at the water-line, and the ice above the notch breaks off in thin lamellas. The resulting calving rate is equivalent to the melt rate at the water-line. This process has been observed on several glaciers and described in detail for fresh-water calving Maud Glacier, New Zealand (Kirkbride and Warren, 1997). Assuming that melting at the water-line is the driving process for calving, the melt rate must be on the order of magnitude of the flow velocity at the terminus. From laboratory and field experiments and from theoretical studies on the deterioration of icebergs, an equation for the melt rate M _w at the water-line per °C water temperature above the melting point was derived (El-Tahan and others, 1987):

(5)

where M _w is in m s⁻¹K⁻¹, H is the wave height in meters, P is the mean wave period in seconds and R is the roughness height of the ice–water boundary in meters. The melt rate is controlled by wave activity and water temperature. According to the literature, a reasonable value for surface roughness of ice in sea water is 1 cm. Assuming a sea temperature of 1°C, a wave height of 0.1–0.2 m and a wave period of 3–5 s, melting rates of 0.2–0.5 m d⁻¹ are calculated (Equation (5)), corresponding to annual melt rates up to 180 m a⁻¹. If the sea is covered with ice during the winter season, no melting will take place at the water-line and therefore the annual value will be reduced. Thus, for slowly flowing tidewater glaciers, melting at the water-line seems to be a controlling process of the calving rate. This is confirmed by observations at Hansbreen, a tidewater glacier in Spitsbergen (Fig. 1; Jania, 1988). Salinity additionally affects melting and may explain the reduced calving rates for small freshwater calving glaciers (Funk and Röthlisberger, 1989).

Fig 1. Calving front of Hansbreen, a tidewater glacier located in Spitsbergen, Svalbard. The notch melted out at the waterline shown in the photograph extended all along the calving face and persisted throughout the melting season. The height of the calving face on the section shown is 18–25 m. The photo - graph was taken at low tide in July 1998.

2.2. Basal sliding

The fast flow observed at many tidewater glaciers (Meier and Post, 1987) is primarily due to high sliding velocities (Clarke, 1987; Kamb and others, 1994; Meier and others, 1994). Also, for small slowly flowing tidewater glaciers, such as Hansbreen, basal sliding dominates the flow in the terminus region (Vieli and others, 2000). Basal water pressure is recognized as an important controlling factor for basal sliding (Budd and others, 1979; Iken, 1981; Bindschadler, 1983; Jansson, 1995). A commonly used description for basal sliding is (Bindschadler, 1983):

(6)

where the basal velocity v _b is related to the basal shear stress τ _b, and k, m and r are adjustable empirical positive parameters. The effect of the effective pressure p _e, which is defined as the ice-overburden minus the basal water pressure, is included in the sliding relation. Water storage at the bed may also be an important factor in basal motion. For short-term velocity variations at Columbia Glacier (Kamb and others, 1994) and at Le Conte Glacier (personal communication from K. Echelmeyer, 2001) the sliding velocity was related to water storage rather than directly to water pressure.

The inverse proportionality of the sliding velocity v _b to in Equation (6) has a strong effect on the flow of tidewater glaciers. The basal water pressure of a tidewater glacier undergoes seasonal and long-term variations, depending on the water input and the state of the subglacial water drainage system. The water level within a tidewater glacier decreases towards the calving front to a value corresponding to sea level. In the situation of a tidewater glacier the effective pressure is also expected to decrease towards the terminus.

According to the sliding law (Equation (6)), the reduced effective pressure induces increased sliding velocities. This is supported by the observed high sliding rates (Meier and Post, 1987) and increased flow velocities towards the calving front on tidewater glaciers, such as Hansbreen (Vieli and others, 2000) , Columbia Glacier (Krimmel and Vaughan, 1987), Glaciar Moreno (Rott and others, 1998), and Nordbo- gletscher, Greenland (Funk and Bösch, 1990). Vieli and others (2000) used a water-pressure-dependent sliding law in a glacier flow model to explain the observed velocity increase on Hansbreen. In the evolution of tidewater glaciers a strong interaction takes place between basal sliding and glacier geometry. An increase in basal water pressure or a thinning of the glacier in the terminus region leads to enhanced basal sliding due to the reduction of effective pressure. The velocity increase induced by sliding leads to additional thinning and a further increase in sliding. It is therefore essential to include the effect of water pressure on basal sliding when modelling the dynamics of tidewater glaciers (Van der Veen, 1997a).

3. Model Description

The tidewater glacier model presented in this paper calculates the surface evolution and the two-dimensional flow regime (velocity, strain rate and stress field) for a longitudinal section of a glacier.

3.1. Field equations and flow law

Ice is treated as an incompressible viscous fluid. The equation for mass continuity and for linear momentum can be written as

(7)

and

(8)

where v_i are the velocity components, ρ is the ice density, g_j are the components of the acceleration due to gravity and τ_ij are the components of the stress tensor. The horizontal coordinate is x ₁ = x and the vertical coordinate is x ₂ = z, which is positive in the upward direction. Glen’s flow law (Glen, 1955) relates the deviatoric stresses to the strain rates and can be written as

(9)

where are the components of the strain-rate tensor, and σ_ij are the components of the deviatoric stress tensor and are given by . The effective shear stress τ is defined by . Typical values of the flow-law exponent n = 3 and the rate factor A = 0.1 bar⁻³ a⁻¹ have been used in the model (Hubbard and others, 1998; Gudmundsson, 1999; Albrecht and others, 2000).

3.2. Basal boundary condition

The glacier flow model requires an appropriate boundary condition at the glacier bed to account for basal sliding. For the present flow model the proposed sliding law (Equation (6)) is used, which takes the effective pressure p _e into account and is based on current sliding theories. We set r = 1 and m = 1 so that we get a linear sliding law in τ _b. Relation (6) is implemented in the model by adding a thin soft layer at the glacier base (Vieli and others, 2000). The viscosity of this basal layer has been chosen in order to fulfil the sliding relation (6) for a specific location. A detailed implementation is described in Vieli and others (2000). The effective pressure p _e in Equation (6) is calculated according to the prescribed water level within the glacier, and the basal velocity and basal shear traction result from solving the system of field equations and boundary conditions.

The effective pressure changes in each time-step and has to be calculated from the actual ice thickness and basal water pressure. The basal water pressure along the flowline of a glacier is poorly known, so assumptions must be made. For the model calculations presented in this paper, the water level is assumed to be on sea level which is the lower limit for a tidewater glacier. The water level is usually higher, especially during melting seasons, but in this way the effect of a decreasing effective pressure towards the glacier front is taken into account. Changes in basal topography due to sedimentation in the sea in front of the glacier, or the formation of a terminal moraine, are not considered in the model.

3.3. Surface boundary condition

The time evolution of the glacier surface is calculated. The surface boundary condition for the glacier surface is

(10)

where S(x, t) is the surface elevation, t is the time, is the horizontal and the vertical component of the flow velocity at the surface, and b(x, t) is the surface mass balance. A linear relation is assumed between mass balance b and surface altitude S.

3.4. Calving front and upstream boundary

At the upstream boundary the horizontal velocity v_x (x = 0, z, t) is set to zero from the surface to the bed, but the ice can move in the vertical direction. This means that no ice flux into the model occurs through this boundary. With this boundary condition we are able to simulate an ice-saddle situation.

For the frontal vertical ice cliff standing in the sea or in a lake, the hydrostatic pressure of the water p _w is taken into account:

(11)

where z _o is equal to sea or lake level. The modified flotation criterion (Equation (4)) is used to calculate the position of the calving front. For each time-step, the new terminus is moved to the position where the ice thickness h exceeds the flotation height by the fraction q = 0.15. The ice mass that is removed corresponds to the mass loss due to calving. Following this method, the calving rate is a result of the numerical model and is controlled by both the ice velocity and the surface changes. This is in contrast to earlier models that included ad hoc assumptions for the calving rate. A floating terminus cannot be treated in our model.

In the case of slowly flowing tidewater glaciers, melting at the water-line is important. Therefore, a prescribed calving rate can be included in the model, which is derived from the melt rates at the water-line according to Equation (5).

3.5. Numerical solution technique

The stress and velocity fields are calculated with the commercial finite-element program MARC (MARC Analysis Research Corp., 1997). The code solves the full equations for the velocity and stress fields (Gudmundsson, 1999), based on the finite-element method. A four-node isoparametric quadrilateral Hermann element is used with a bilinear interpolation function. For each time-step, the two-dimensional stress and velocity fields along the flowline are calculated. With the calculated surface flow velocities and the mass-balance input, the new glacier surface is determined by the surface boundary Equation (10). This equation is approximated by finite differences using the two-step Lax–Wendroff method (Press and others, 1996), which is based on a forward-time centered-space scheme and is second-order in time and space. This approximation was used and tested in detail for this application by Leysinger (1998). Nodes at the calving front are moved according to the velocity vector and the time-step. For each time-step, the terminus position is updated according to the modified flotation criterion, and a new grid is defined for the updated glacier boundary. This procedure to determine the new terminus position after a time-step is identical for a retreating and an advancing scenario.

In the following model calculations a time-step of 0.1 year is used and the glacier length is updated at each time-step by using the modified flotation criterion (Equation (4)). To test if the calculated length change and the resulting calving rate are independent of the chosen time-step, the model has been run for the same scenarios with different time-steps. For retreat scenarios, the cumulative change in length obtained since the beginning of the simulation differs by at most 0.3% during periods of fast retreat with time-steps varying between 0.05 and 0.1years. In the slowly retreating periods the maximum difference is <0.05%. We conclude that the model results are not significantly influenced by the chosen time-step.

4. Model Experiments

4.1. Model input

A retreating and an advancing scenario across a submarine basal depression are calculated with the numerical model. A synthetic bed topography is assumed, which should be representative for a tidewater glacier (Fig. 2). The model calculations start with steady-state glacier surfaces obtained from model calculations for prescribed constant mass balances. A typical simplified mass-balance function from a tidewater glacier in Svalbard (Hansbreen) (Jania and Kaczmarska, 1997) is used, in which the mass balance depends linearly on altitude and is constant above a critical altitude h _a (Fig. 3):

(12)

where S(x) is the surface elevation and δb is a parameter to impose changes in mass balance. Numerical values of a ₀ = 0.0061 a⁻¹, a ₁ = −2.3 m a⁻¹ and h _a = 450 m were determined from data of Jania and Kaczmarska (1997). The scenarios are forced by shifting the mass balance by δb (Fig. 3). For the model calculations, a water pressure within the glacier corresponding to sea level is assumed. Seasonal variations of the englacial water level are not included.

Fig. 2. Glacier bed (solid line) and initial surface topographies used for model calculations for the retreating (dashed-dotted line) and the advancing scenario (dashed line). Both steady-state surface profiles are calculated using the same mass balance.

Fig. 3 Parameterized mass balance used for the retreating (dashed-dotted line) and the advancing scenario (dashed line). The solid line indicates the mass balance used to calculate the initial steady-state surface geometries.

4.2. Model results

Retreating scenario

The glacier retreat is forced by shifting the mass-balance function (Equation (12)) of δb = −0.3 m a⁻¹ (Fig. 3) during the entire time period of model calculations. The modelled retreat is shown in Figures 4 and 5. Three different phases can be distinguished. In the first phase, the terminus is slowly retreating until the top of the submarine hill is reached (point A). From this point, the rate of retreat increases as the glacier terminus gets into deeper water, resulting in a very rapid retreat and in high calving rates (second phase). Once the deepest part of the basal depression (point B) has been passed, the glacier terminus moves into shallower water, the rate of retreat is reduced and the situation resembles that of the first phase. With the retreat into deeper water, the calving rate and the velocity at the terminus increase (Fig. 5). However, the calving rate increases faster than the ice velocity, resulting in a rapid terminus retreat. Although the ice thickness decreases, the surface flow velocity increases significantly along the flowline towards the calving front over the entire retreating period (Fig. 6). This is mainly due to increased basal sliding near the front, caused by the decreasing effective pressure. In the terminus region the ice flow velocities undergo large changes over time due to changes in basal sliding, whereas further up-glacier the velocity changes are small (Fig. 6). During the phase of rapid retreat strong surface lowering takes places (Fig. 4), leading to high calving rates (Fig. 5b).

Fig. 4. Evolution of the glacier surface for the retreating scenario. The time interval between two surface profiles is 50 years. The dashed line is the starting surface. The top of the bedrock hill and the deepest point in the basal depression are indicated by A and B, respectively.

Fig. 5. Retreating scenario: evolution of (a) the glacier length L, (b) the calving rate u _c , the velocity at the terminus u _i and the length change dL/dt and (c) the water depth d at the terminus between 800 and 1300 years.

Fig. 6. Retreating scenario: (a) glacier bed elevation along the flowline and front position (same as Fig. 4); (b) contour plot of temporal evolution of the surfaceflow velocity along the flowline. The contour line interval is 10 m a⁻¹.

The mass-balance function was shifted at the beginning of the calculations but then kept constant as a function of altitude for the whole model period, corresponding to constant climatic conditions. The sudden rapid retreat takes place at the location of the basal depression after a period of 1100 years of constant mass-balance function or constant equilibrium-line altitude (ELA) (Fig. 7). Thus, the change in glacier length does not immediately reflect the climatic signal. Although the input mass-balance function is constant over time, the average surface net balance (surface accumulation and ablation without calving) undergoes changes due to changes in surface elevation and geometry (Fig. 7b). During the phase of rapid retreat, the ablation is dominated by calving and leads to a rapid shrinkage of the ablation zone, which is the cause of the sudden increase in the accumulation–area ratio (AAR) and the average surface net balance (Fig. 7c and b). This illustrates that a time series of average surface net balance of a glacier must be used with care if interpreted as an indicator of changes in climate.

Fig. 7. Mass-balance changes over time for the retreating scenario. At time zero the shift in the mass-balance function was performed and the model calculations were started. (a) Glacier length over time, (b) Met balance, surface net balance (surface accumulation and ablation without calving) and ablation by calving are shown over time as values averaged over the glacier area. (c) AAR over time. (d) ELA as an index for the input mass-balance function over time.

Advancing scenario

A glacier advance is forced with a shift of the mass-balance function (Equation (12)) of δb = +0.9 m a⁻¹ (Fig. 3). The glacier is thickening due to the positive mass balance and slowly starts to advance (Figs 8 and 9). While the glacier is advancing, the calving front reaches deeper water, leading to higher calving rates and ice velocities at the terminus. The rate of advance is very small and decreases with increasing water depth. Once the terminus passes the deepest point of the basal depression (B), the calving rate decreases rapidly, accompanied by a smaller reduction of the terminus velocities. This results in a rapid advance until the terminus overrides the basal hill (A). For a short period of time, the calving rate even vanishes because the terminus slides uphill, and the critical height above buoyancy h _c is always exceeded during this step. Throughout this phase, processes other than the flotation criterion may control the calving rate.

Fig. 8. Evolution of the glacier surface for the advancing scenario. The time interval between two surface profiles is 20 years. The dashed line is the starting surface. The top of the bedrock hill and the deepest point in the basal depression are indicated by A and B, respectively.

Fig. 9. Advancing scenario: evolution of (a) the glacier length L, (b) the calving rate u _c , the velocity at the terminus u _i and the length change dL/dt, and (c) the water depth d at the terminus.

For this reason, an additional model run with the same scenario was performed, which included melting at the water-line (Fig. 10). A constant melting rate at the calving front was assumed (Equation (5)), resulting in a constant calving rate . This prescribed melt- induced calving rate is only considered if the calving rate inferred from the flotation criterion drops below 80 m a⁻¹. This is the case during the rapid advance. Due to the prescribed calving rate during this phase, the rate of advance is slightly reduced at the beginning of the accelerated advance (Fig. 10), but the height above buoyancy at the terminus starts to grow and exceeds the critical height h _c. This leads to higher frontal flow velocities. Once the terminus has passed the frontal moraine and reaches deeper water, the buoyancy- induced calving is again controlling the front position change. Despite the different change in length during the fast period of advance compared to the case without a prescribed melt-induced calving rate, the final positions of the glacier front are almost identical (Fig. 10).

Fig. 10. Different advancing scenarios, (a) Evolution of glacier length. The solid line represents the case of the advancing scenario with a prescribed melt-induced calving rate of 80 m a⁻¹. The dotted line shows the advancing scenario without a prescribed calving rate (same as in Fig. 9) and the dashed line is the advance scenario with reduced mass-balance shift of 0.7 m a⁻¹instead of 0.9 m a⁻¹. (b) Calving rates corresponding to the advance scenarios shown in (a).

In an additional model run with a slightly smaller shift of the mass-balance function of δb = +0.7 m a⁻¹ instead of 0. 9 m a⁻¹, it is not possible for the glacier to overcome the basal depression (Fig. 10). A steady state is reached already in the downslope region of the depression.

Sensitivity of the model results

To examine the sensitivity of the modelled scenarios to the choice of the height above buoyancy, additional model runs with a slightly different q were performed (Fig. 11). A larger q = 0.18 instead of q = 0.15 leads to higher calving rates and frontal flow velocities and therefore to a higher mass loss by calving, whereas a smaller q = 0.12 leads to a reduced mass loss by calving. The retreat rates are not changed significantly, but the onset of rapid retreat is shifted in time, though still fixed to the location of the basal depression. Retreating scenarios are only affected to a minor degree by changing q, whereas advancing scenarios show a qualitatively different behaviour. For the advancing scenario a reduced q = 0.12 results in a faster advance, because with respect to q = 0.15 the mass loss by calving is reduced. However, the general advance behaviour with respect to basal topography is similar. With q = 0.18 in the advancing scenario, the terminus does not overcome the basal depression, because the mass loss by calving is too large and a steady-state geometry is reached. In contrast to the case of retreat, the total mass loss by calving is also high during the phase of slow change in position. For this reason, a change in q has a significant effect on the change in the terminus position for the advancing scenario.

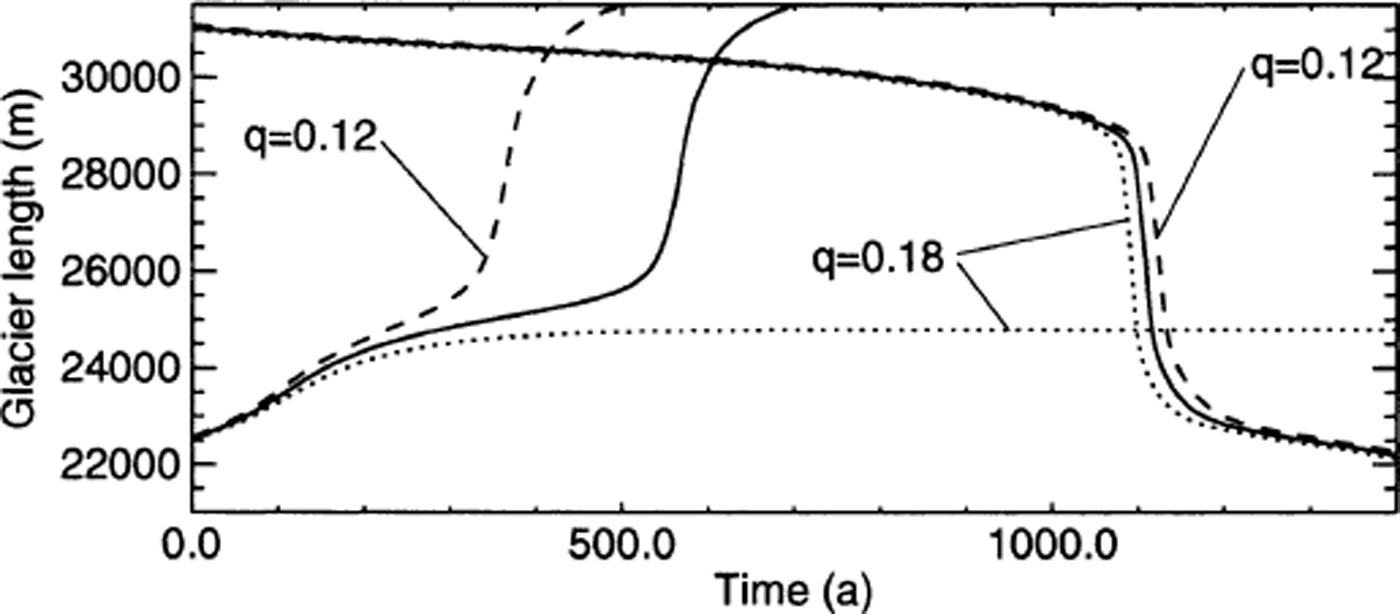
Fig. 11. Retreating and advancing scenarios with variable height above buoyancy. The solid line represents the modelled evolution of the glacier length presented before (q = 0.15), and the dashed and dotted lines show the evolution of glacier length for a slightly different height above buoyancy with q = 0.12 and q = 0.18, respectively.

A 10% increase or reduction in water depth in the region of the basal depression results in a dynamical behaviour qualitatively very similar (Fig. 12) to that presented before with varied q (Fig. 11). The magnitude of the rate of retreat or advance is different in the region of the basal depression, because the calving rate is sensitive to changes in basal slope and water depth. In the case of the shallower depression, dL/dt is reduced during the phase of rapid retreat due to a reduced mass loss by calving, whereas for the deeper depression the rapid retreat is accelerated as a result of enhanced calving. In the advancing scenario with increased water depth the glacier does not overcome the basal depression, because the mass loss by calving becomes too large.

Fig. 12. Retreating and advancing scenarios with variable water depth in the region of the basal depression. The solid line represents the modelled evolution of the glacier length presented before, and the dashed and dotted lines show the evolution of glacier length for a change in water depth in the region of the basal depression of −10% and +10%, respectively.

These sensitivity considerations on the critical height above buoyancy and the magnitude of the basal depression confirm the effect of basal topography on the dynamics of tidewater glaciers obtained from the previous advancing and retreating scenarios. Nevertheless, in the advancing case a variation of q or the magnitude of the basal depression can have a significant effect on the qualitative behaviour of the glacier evolution.

5. Discussion

The modelled relation between calculated calving rate and water depth using the modified flotation criterion (Equation (4)) is qualitatively in good agreement with the linear relation suggested from observations (Brown and others, 1982), but only regarding slow advances or retreats (Fig. 13a and b). Where rapid changes occur the calving rate increases non-linearly with water depth. Meier and Post (1987) showed that the linear calving law is probably limited to the case of slowly changing tidewater glaciers by arguing that in the case of rapid retreat, flotation may be the determining factor. This is also supported by the data from rapidly retreating Columbia Glacier (Van der Veen, 1996), and our model results clearly confirm this limited validity of the linear calving law.

Fig. 13. Calculated calving rates plotted against water depth for (a) the retreating scenario and (b) the advancing scenario. Each cross or diamond corresponds to the calculated values for a time-step of 1 year. The numbers denote the time evolved in years. The diamonds mark periods of rapid front position changes which take place between 1080 and 1140 years for the retreat and between 520 and 600 years for the advance scenario.

Considering the flotation criterion for the calving process, the retreat or advance is primarily a consequence of glacier thinning or thickening in the terminus region, which is in general due to mass-balance changes. The magnitude of the thickness and therefore the length change depends, besides the mass balance, on bed geometry and basal sliding. For example, during the rapid retreat through the basal depression, the typical flow acceleration towards the calving front is enhanced, because basal sliding increases with water depth (Fig. 6). This leads to a much higher mass-flux divergence in the frontal region and finally to an additional surface lowering.

In the presence of a basal depression, a small change of mass balance can lead to a drastic change in the terminus position. It could be shown that thinning due to a slightly negative mass balance is the triggering process for a rapid retreat. This result supports the concept of Van der Veen (1996) for explaining the observed rapid retreat of Columbia Glacier, which suggests that the rapid retreat is initiated and maintained by the thinning of the glacier. The model calculations demonstrate that rapid changes of tidewater glaciers are, as often observed, predominantly an effect of bed topography at and behind the terminus, and only to a minor degree a direct reaction to a mass-balance change. This was already described qualitatively on the basis of observations by various authors (Meier and Post, 1987; Warren, 1993; Naruse and others, 1997).

The model calculations performed with the two scenarios confirm the concept of rapid retreat and slow advance of a tidewater glacier through a basal depression qualitatively described by Meier and Post (1987). The obtained simultaneous increase in terminus velocity with increasing calving rate illustrates that an accelerated retreat through a basal depression is not obvious. The model experiments performed clearly show that whether a retreat or advance is slow or fast depends not only on the water depth, but also on the sign of the basal slope at the terminus. Rapid changes in the terminus position occur where the bed slopes up in flow direction, whereas in regions where the bed slopes down the changes are slow.

In contrast to the slow advance with progression into deeper water, a fast advance into shallower water is predicted by the model. This has been observed qualitatively at Taku Glacier (Motyka and Post, 1995) and Hubbard Glacier (Mayo, 1989), but, in both cases, sedimentation processes and the formation of a terminal push-moraine were involved in the rapid advance.

The model results enable us to identify regions of stable and unstable terminus positions. A downsloping bed in the flow direction allows a stable or slowly changing position. On the other hand, if basal elevation increases in the flow direction, the terminus position is not stable and a rapid retreat or advance to a stable region is inevitable. As a consequence, in the presence of a basal depression in the terminus region of a tidewater glacier, more than one steady-state surface and terminus position exists for a given mass balance, depending on the initial geometry. In Figure 2 two different steady-state geometries calculated with the same mass balance are shown. The lower steady state was calculated with an initial terminus behind the basal depression, whereas for the other steady state it was in front of the basal depression.

In the case of a progression of the terminus into deeper water, the rate of advance slows down, because the mass loss due to calving increases. Thus, a long time is required to build up enough mass to advance. The model results of the advancing scenario show that in order to overcome a basal depression, a long period of large positive mass balance is required. If the mass balance is not large enough, the glacier will reach a steady state and the calving front will stay in the downslope region of the depression (Fig. 10). For deep basal depressions, such as those beneath Columbia Glacier, a very large positive mass balance over very long time periods (>1000 years) may be expected as a necessary condition for a readvance across the depression. Looking at the long time periods needed for the advance through a bed depression, other processes may support the advance of the glacier terminus. For example, rock sedimentation in the glacier forefield and the formation of morainal banks would reduce the water depth and the calving activity and facilitate an advance (Paterson, 1994; Motyka and Post, 1995; Fischer and Powell, 1998). These processes are not considered in the presented dynamic model, which poses a limitation to modelling an advance of a tidewater glacier.

Other processes, such as lateral drag or cross-section changes along the flowline, may be important. For example, a narrowing of a valley or an increase in lateral drag may lead to a slower retreat of a tidewater glacier. However, such three-dimensional processes and the possible onset of floating of the ice tongue cannot be treated in the present model.

6. Conclusions

Advance and retreat of the terminus of rather small and slowly flowing grounded tidewater glaciers are simulated with a numerical glacier model. The model solves the full force-balance equations to compute stress and velocity fields and calculates the time evolution of the glacier surface for a given mass-balance scenario. Basal sliding is implemented through a sliding parameterization based on basal water pressure corresponding to a water table at sea level. Calving is implemented with the flotation model, in which the calving front is shifted at each time-step to the position where the frontal ice thickness exceeds flotation height by a prescribed value. Thus, the calving rate is an output of the model, in contrast to previous modelling approaches. For slowly flowing glaciers which are considered here, other processes such as melting along the water-line at the calving front may become controlling processes. Therefore, a calving rate equivalent to the melting rate can additionally be prescribed in the model.

The model calculations confirm the cycles of slow advance and rapid retreat through a basal depression suggested by Meier and Post (1987). For a slowly advancing or retreating situation, the known empirical relation between water depth and calving rate (Brown and others, 1982) is qualitatively reproduced by the model, but not for rapidly changing situations. Thus, this study demonstrates that unstable rapid retreats of tidewater glaciers and the known empirical relation between calving rate and water depth can be explained with a model in which a height-above- buoyancy criterion is prescribed.

The model calculations further show that calving depends not only on water depth but also on the sign of the basal slope in the terminus region. Rapid changes of the terminus positions preferably occur in regions where the bed slopes up in the flow direction, and are therefore predominantly an effect of bed topography rather than a direct reaction to changes in climate. In our model experiments, thinning due to a change in climate and therefore in mass balance is only the triggering process for a rapid retreat through a basal depression.

If buoyancy, parameterized with the flotation criterion, is the dominant driving factor for calving, the obtained rate of advance or retreat is primarily controlled by changes in the surface elevation in the terminus region, and much less by the calving mechanism itself. This means that the magnitude of the calving rate is a result of the glacier dynamics and not vice versa. Surface-elevation changes near the terminus are strongly affected by changes in basal sliding and bed topography. This sensitivity of glacier change to basal topography has important consequences regarding the future behaviour of tidewater glaciers with respect to climate change. A simple parameterization in terms of easily available information, such as surface topography, ice-flow velocity and terminus height, cannot be expected. Since basal depressions in the frontal region are typical for tidewater glaciers, rapid retreats are likely, even if the mass-balance changes are small and slow. To predict the length change of tidewater glaciers, especially for short-term changes, the basal topography in the frontal region must be known.