Introduction
This article is divided in four parts. In part I we derive a system of partial differential equations, which describe fractionation between ideal solid and liquid solutions in a melting column with percolating liquid phase. Although the equations apply equally well to all ideal solutions, we establish the nomenclature of the problem suitable for the present work. So we consider particularly the exchange of HDO and H2O molecules between ice and water in a snow column of a melting temperate glacier.
In part II we present finite difference equations deduced from the partial differential equations and give a precise description of the method of numerical solution.
Part III deals with the comparison of numerical solutions of the equations with measurements in the laboratory and on glaciers. Special attention is drawn to the exchanges of HTO and H2O in glaciers. The results of the computation are in good agreement with measurements.
In part IV we discuss the quality of the model and equations and some possible improvements are considered.
List of main symbols

I. The partial differential equation
Ideal solid column, melting, precipitation and percolation
We make the following assumptions
-
(a) Melting is occurring only at the top of the column. We let the coordinate system move to maintain x = 0 at the top of the column for all t.
-
(b) We assume the same total number of H2O and HDO molecules per unit height for all sections of the column:
(1)
where K is the total number of HDO and H2O molecules in the liquid phase per unit height, K′ is the total number of HDO and H2O in the solid phase per unit height, K and K′ being constants.
-
(c) The precipitation is uniform for all t:
(2)
where K t is the total number of water molecules in liquid precipitation filtering into the column in unit time, K t being constant. We do not expect sublimation from the top surface of the column to be of any importance.
-
(d) Melting is uniform for all t. With (a)–(c) this means that the column in the defined coordinate system is moving upwards with constant velocity
 . Also the percolating liquid is flowing down the column with constant velocity
. Also the percolating liquid is flowing down the column with constant velocity  . This gives us the continuity equation:(3)
. This gives us the continuity equation:(3)
For convenience we let

thus v is the ratio of solid precipitation to total melting of the solid phase, λ is the ratio of total liquid precipitation to total melting, η is the ratio of solid phase to liquid phase in the section, ft is the ratio of total liquid precipitation to total solid precipitation.
-
(e) Along with the percolation of liquid phase there is continuous exchange of HDO and H2O between the solid phase and the liquid phase. The equation of continuity gives in every section:
(5)
and
(6)
We use the bar to indicate changes due to fractionation in the time ![]() to
to ![]() for a section Δx thick at depth x. The following simple law for the fractionation is assumed:
for a section Δx thick at depth x. The following simple law for the fractionation is assumed:
where τ is a time constant.
Equation (7) is a crucial assumption for our derivation, and is equivalent to assuming exponential decay into phase equilibrium, which is the simplest approximation to make. This may seem a very awkward assumption, since molecular diffusion in ice crystals is known to be extremely slow, which should render this process irrelevant (Reference ItagakiItagaki, 1967). The mechanism despite this is suggested to be continuous melting and recrystallization of the solid phase along with percolation of the liquid phase under adiabatic conditions. Changes in the grain size of the snow are actually observed both on temperate glaciers and in laboratory experiments, supporting the hypothesis of melting and recrystallization.
Now

and

Equations (7a), (7b) and (7) combine to give

In natural water N/K ≈ 150 × 10−6 ≈ N′/K′, suggesting the approximations K–N ≈ K, K′ ≈ N′ ≈ K′, and 1+u ≈ 1 ≈ 1+v be made, implying

As before we use the bar to indicate the changes due to the fractionation law described by Equation (7).
The equation of isotope fractionation in a melting ideal solid column with percolating liquid phase
Consider the variation of the number NΔx of HDO molecules in the liquid phase in the section ![]() to
to ![]() in time
in time ![]() to
to ![]() (Fig. 1). The time variation of the number is caused by:
(Fig. 1). The time variation of the number is caused by:
-
(a) The different isotope ratios for the liquid phase flowing into the section and out of the section, and
-
(b) Fractionation as described by Equation (9).

Fig. 1. Coordinates used in deriving the equations.
We then have

Dividing by ΔxΔt K ≈ ΔxΔt(K–N) and using the same approximation as in Equation (9),

In a similar way we obtain for the HDO molecules in the solid phase:

Choosing the total melting height of the snow column as unit height y = vx, (Fig. 2) the equations become



Fig. 2. Comparison of the spring and fall values of coordinates used in deriving the equations.
The boundary values and initial conditions for the isotope ratios
The boundary values of isotope ratios in our case are determined by the isotope composition of the precipitation W (t), the isotope ratios of the solid phase on top of the column v(0, t), and the ratio of the amount of precipitation per unit time to the amount of melted solid phase per unit time. This ratio is λ.
The equation of continuity (for the rarer isotope) at the top of the column implies:

η, κ, λ and ϕ are not independent parameters as may be seen from Equation (3) and (4).

It is convenient to choose η, λ and ν as parameters of the equations and conditions, thus
The natural initial condition is a pure solid-phase column (no liquid phase). No changes take place in any section before the percolating liquid phase reaches that section. This frontier of percolating liquid phase determines an initial boundary of the domain of the equations. At the time the percolating liquid phase reaches a particular section, the height of the column may have diminished.Footnote * This can be described by the initial condition for our equations.
where


for ![]() .
.
Summary of the partial differential equations, boundary values and initial conditions The partial differential equations:



The domain of the equations is shown in Figures 3 and 4.

Fig. 3. The domain of the equations is shaded. In the case illustrated the column does not melt totally.

Fig. 4. The domain of the equations is shaded. In this case the column melts totally.
Boundary value:
Initial condition:

Isotope ratio of draining water
The isotope ratio of the liquid phase draining from the bottom of the column is given by u(y, t) on line segment:
Solutions of the partial differential equations
The equations are the well-known telegraph equations, but the above mixed boundary and initial-value conditions are unusual. We have proved the existence and uniqueness of the solutions with these conditions.
In the proof use is made of Riemann’s method. Define h = v for x = 0. Using Riemann’s method there emerges an integral equation for h of the type ![]() , where f is a known function and
, where f is a known function and ![]() is an integral operator:
is an integral operator:
We use the norm ||h|| = sup 0 ⩽ x ⩽ a h(x). The operator ![]() has an unique continuous inverse if
has an unique continuous inverse if
It was shown that ![]() for all a < a
max where a
max > 1.
for all a < a
max where a
max > 1.
II. Difference equations
Equation of finite differences
Finite difference methods will now be employed to produce a numerical solution of the partial differential equations. The difference equations can be derived directly from the differential equations. Let us first make the transformation:
The differential equations become

where U(s, t′) = u(y, t) and V(s, t′) = v(y, t).In this coordinate system the bottom of the solid phase column will remain fixed. The liquid phase is percolating with velocity 1+κ.
Consider all points with coordinates ![]() , where k and i are integers (> 1) and h and g positive numbers. We define two neighbours to an arbitrary point
, where k and i are integers (> 1) and h and g positive numbers. We define two neighbours to an arbitrary point ![]() namely:
namely:
and
Equations of finite differences may then be written as

where we have chosen h/g = (1+κ) implying that P and Psw become points on the same characteristic line.
These equations make it possible to compute U and V for all points ![]() , when the values for
, when the values for ![]() are known (Fig. 5). Note that P and Ps are also points of the same characteristic line. The Equations (16′) and 17′ can easily be translated into physical language. Equation 16′ tells us that a liquid phase cell at point P was at point Psw
g time units earlier. The changes of the isotope ratio of the water are due to the decay towards equilibrium with the solid phase at Psw.
are known (Fig. 5). Note that P and Ps are also points of the same characteristic line. The Equations (16′) and 17′ can easily be translated into physical language. Equation 16′ tells us that a liquid phase cell at point P was at point Psw
g time units earlier. The changes of the isotope ratio of the water are due to the decay towards equilibrium with the solid phase at Psw.

Fig. 5. When applying the difference scheme the domain can be described by meshes as illustrated.
A general computer programme for solving the differential equations was not available at the Computer Center of the University of Iceland. A programme had therefore to be written. In describing the difference scheme it is found useful to rely heavily on the physical characteristics of the problem rather than follow the equations in a straightforward manner.
Description of the computations
Let us divide the length dimension (depth of the snow column) into R increments (R > 2) and the time dimension (the melting period) into S increments. The R increments will be termed cells of the column and the S increments showers. The rain is modelled as a row of showers. The ratio of the length and time increments is chosen such that the water column moves down a cell during a shower. At same time 1/(κ+1) of the top snow cell is melting (κ is an integer > 1). We choose S and Q. such that S = (κ+1) Q. Q. is the total number of snow cells melting during whole process. If Q = R the column is completely melted.
Initially the column consists of solid phase only.
v(k, 0), where (1 ⩽ k ⩽ R) is the isotope ratio of the kth cell from the top at the start of the process. v(k, i) is the isotope ratio of solid phase in the kth cell after the ith time interval. u(k, i) is the isotope ratio of the water phase in the kth cell after the ith time interval. w(i) is the isotope ratio of the ith shower. x(i) is the isotope ratio of the liquid draining from the column in the ith time interval.
Let i = 1:
During the first shower 1 /(κ+1) units of the top cell will melt and mix with the liquid precipitation filling up κ/(κ+1) of the top cell with liquid phase.

It is convenient to use following notations:

where p and q are defined by i = q(1+κ)+p+1, 0 ⩽ p ⩽ κ.
Let q+2 ⩽ R, i > 2, p ≠ k, then
For p = κ, the top cell is emptying and therefore it makes nonsense to compute using Equations (28) and (29). To find the isotope ratios for the lower cells, we have two possibilities:
(I) i ⩽ R, and (II) i > R.
(I) i ⩽ R (Fig. 6)

Fig. 6. The difference scheme makes uses of “cells” and “showers”, which can be made plausible by columns of squares as shown in the drawing. In the situation illustrated the percolating liquid phase has not reached the bottom of the column.
The percolating liquid phase has not yet reached the bottom of the column and the rest of the column must be treated in three different sections:
-
(a) q+2 < k < i ⩽ R
(32) (33)
(33)
-
(b) q+2 < i = k ⩽ R
(34) (35)
(35)
-
(c) q+2 < i < k ⩽ R
(36)
(II) R < i (Fig. 7)

Fig. 7. The liquid phase has reached the bottom of the column and drained liquid portions are present.
The percolating liquid has reached the bottom of the column and liquid is draining from the column.
-
(a) q+2 < k ⩽ R < i
(32) (33)
(33) (37)
(37)
We must take special care of the case when the column melts totally, i.e. q+2 = R and q+1 = R may be satisfied.
-
(b) q+2 = R < i
The column has only two cells left. Isotope ratios of these cells are already determined by Equations (28) to (31). The isotope ratios of the draining liquid is as before:
We are now left with the case q+1 = R < i, which means that the last cell is melting:

The case Q = R, i = S leaves us with the column filled up with liquid phase. To find the final pure solid-phase column we must let the liquid percolate through.
Define i = S+j, 1 < j < R–Q. The upper boundary of the liquid phase divides the column into three sections:
-
(a) Q < k < Q+j ⩽ R
(36)
-
(b) Q+j ⩽ k ⩽ R
(32)
-
(c) Q+j < k ⩽ R
(33)
For all is we have:
Commentary on the computer programme
The programme needs considerably less core storage if we define the vectors:
The vectors v 1(k) may at every time instant be computed from the known veclors v 2(k), u 2(k). Before advancing in time the old vectors may be replaced by the new ones, i.e.

without destroying any information essential for further computation.
The following changes of formulas are necessary:

A flow chart for the programme is shown in Figure 8.

Fig. 8. The flow chart of the computer programme.
III. A comparison of computed results and measurements
1. Melting snow column in laboratory
A glass cylinder (60 cm high) was filled with fine-grained soft snow. The outer surface of the tube was insulated with asbestos fibres and kept at 0° C (Reference ÁrnasonÁrnason, 1969[b]). The column melted gradually from the top. When about a fifth of the column had melted, water started to drip from the bottom of the column. This determines the parameter η in our equations for this model; η = 4.0. The ratio λ = 0.0 since rain was not simulated. In the laboratory experiment the column melted totally so v = 1.0. The only remaining parameter of our equations is τ, the time constant. From computations we got the best fit with the measurements when τ = 0.18 (Figure 9). The total melting time was about 3 h so τ is near 30 min in this case. The agreement with experiment is excellent.

Fig. 9. Comparison of results from laboratory experiment and the equations. The concentration of drain water samples is shown versus fraction of melted snow. The fit is excellent except for the first three observations. This discrepancy could be caused by some portion of the first melt water flowing down the inner surface of the glass tube instead of percolating down the snow column.
2. Measurements of deuterium ratios on temperate glaciers
Consider a snow column of a temperate glacier. Measurements of springtime samples show a considerable variation of deuterium ratios in winter precipitation. During summer, the snow melts on top of the column, and rain, condensation and melt water percolate down the column. Our model should be applicable to these conditions.
Figure 10 shows the results of computations for three different pairs of the parameters λ and ν. η is assumed to be 8.0 in all cases. Deuterium ratios of winter and summer precipitation are assumed to be constant:

Fig. 10. The drawing shows the influence of changing parameters of the equations. The concentration of snow samples is drawn versus relative depth.
(SMOW = standard mean ocean water).
τ is also assumed to be the same for all cases τ = 0.1.
Actually there is considerable difference between deuterium concentrations of winter and summer precipitation. On Vatnajökull (site VI) the mean deuterium concentration of winter precipitation is δ w = −81.4‰ and the mean concentration of the annual precipitation is estimated to be δ y = −78.2‰ (Reference ÁrnasonÁrnason, 1969[b]). This implies the relation:

where μ is the ratio of summer precipitation to winter precipitation and δ s is the mean deuterium concentration of summer precipitation. Figure 11 shows results of computations following our model for four pairs of ν and μ and for comparison the results of measurements of samples from site VI on Vatnajökull (τ = 0.01).

Fig. 11. The figure demonstrates the best fit to observations in a section in a bore hole on Vatnajökull. Concentration is drawn versus relative depth.
3. Measurements of tritium concentrations
Concentration of tritium in precipitation is independent of the concentration of deuterium. The periodic variation of tritium concentrations is a very marked feature. The fractionation constant is assumed α T = 1.024Footnote * (Reference JonesJones, 1968). Comparison of the results of our model for these two isotope exchanges is therefore a crucial test of the applicability of our model. Unfortunately we do not have the data needed for both isotopes from any single place.
Figure 12 shows the results of our model applied to the precipitation on the glacier Langjökull in the period October 1965 to September 1966. We use information on tritium concentration of precipitation at Vegatunga in central southern Iceland,Footnote † and assume accumulation of snow on the glacier at 1 300 m above sea-level to start in October and end in May. The mean tritium concentration of the snowfall column for 1966 is shown in the figure for comparison. The parameters used are η = 8.0, v = 3.0, λ = 0.583 and τ = 0.01.
Bearing in mind, that information from Vegatunga and Vatnajökull are not to be expected to be completely applicable for Langjökull, the result is only expected to be qualitative and the result is striking.

Fig. 12. The equations give a satisfactory qualitative explanation of the trends of tritium concentration in snow samples on Langjökull. The changes of the tritium concentration of the snow as shown in the central part of the figure are marked.
IV. Discussion and conclusions
-
(a) The parameter η is the ratio between total number of water molecules in the liquid and solid phase in a section of the column. We assume η to be constant throughout. Nature does not satisfy this condition. In heavy rainfall this ratio becomes much higher at the top of the column than deeper under the surface, where it is reasonable to make this assumption, η will depend heavily on the grain size and will therefore change with time, since according to observations the grain size increases with percolation and time. This parameter in the equations must therefore represent a mean value and should be expected to remain similar for all cases on temperate glaciers. Occasional ice layers will of course influence the applicability of our model. It is reasonable to assume 2.0 < η < 20.0.
-
(b) The parameter λ is the ratio of liquid precipitation per unit time to quantity melted per unit time. An effective factor in the melting of glaciers is condensation of moisture onto the cold surface of the snow. This effect per se would imply λ to be a simple function of total melting. Melting by convection destroys this relation and therefore we must depend on approximation, experience, or direct measurement.
-
(c) The parameter τ. For convenience the total melting time was selected as unit time. Any other choice of time unit would only affect the Equations (11) and (12) by a factor of τ. A straightforward interpretation of τ in the context presented is to assume the value of τ simply as a fraction of the total melting time. One has to bear in mind the simplifications assumed. First melting and liquid precipitation are assumed continuous and constant. Of course both are discontinuous. Due to the hyperbolic character of the differential equations the discontinuous periods can be assumed to follow each other closely without destroying any physical details of the column. Adding up the (most effective) discontinuous melting periods the effective melting time (T eff) is obtained. The condition of continuous and constant rate of melting and precipitation implies constant percolation, which again implies another possible approach to the problem. The essentials of the fractionation process depends on the time T′ it takes a single drop of liquid to percolate from top to bottom of the solid column or the time of contact between the drop considered and the solid-phase column. The first liquid to drain from the melting column is expected 1 /(κ+1) time units after the start of melting. Implying the relation
T′ will depend on the total height h and the velocity of percolation v, say 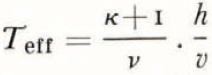 const.
const.
Comparing two cases with different characteristic parameters and different actual heights, the two time constants should be related:
The velocity of percolation depends on grain size and packing and therefore changes with time. It also depends on the rate of melting and volume of precipitation. Altogether we may conclude that τ must be a complicated function of physical characteristics of the melting conditions. Though Equation (41) is expected to be an applicable approximation containing only fairly well defined quantities. For example, compare τ 1 = 0.18 as considered in part III, case 1, and τ 2 = 0.01 considered in part III, case 3. Other parameters are
and
respectively, h 1 was 60 cm, h 2 may be assumed to be about 5 m. Using Equation (41) we find the ratio of τ 1 to τ 2 to be 7.6 v 1/v 2.
The order of magnitude is right, and the difference may be explained as due to different velocities of percolation. A factor two for the ratio v 1/v 2 seems to be reasonable because the percolation in the laboratory experiment is forced by fairly fast melting (reflected in a small value of η 1).
(d) The parameter v. The parameters η, λ and v should be easily estimated for each particular case, when some experience has been gathered in using the equations. Measurements of isotope concentrations of samples collected in autumn should then be sufficient to determine v, and then also the solid precipitation of the previous winter. By looking for best possible fit, the value of λ could be corrected, and the precipitation of the whole year estimated.
(e) The equilibrium constant α. As stated above we use the value α = 1.0208 (Reference ÁrnasonÁrnason, 1969)[a]). The constant as measured under ideal condition in the laboratory is not necessarily an appropriate choice. Measurement of deuterium concentrations of ice at the side of fountains in winter gave lower concentrations than expected from the laboratory experiment. Thus we obtained α eff = 1.014. This can be understood as a result of quicker freezing than the diffusion in solid ice and movement of water in the fountain can cope with to maintain equilibrium conditions. This may be described by assuming the decay time constant involved.
Considering the problem of ice at the side of fountains, for a crude description assume the simple law expressed in Equation (7)
to be valid. Let u be constant. Then
Define the mean time of exposure, t mean, as the time each crystal unit is exposed to water before it is covered by a solid film and define α eff as the ratio

Obviously 1 ⩽ α eff ⩽ α since t mean will depend on the rate of freezing. We choose to operate with an ideal value of α.
When the difference between isotope ratios of percolating liquid and the solid column is small, the most obvious effect of the present model of fractionation processes is to affect the difference such that the isotope ratio of the solid phase tends to be about 2% higher than in the liquid phase, even though one does not expect equilibrium conditions to be reached.
If the difference on the other hand is large and isotope ratios variable the most striking effect is to level the variations and reduce the difference.
Only the first effect is due to the presence of fractionation constant. The second effect is also implied when α = 1.00 and is effected by continuous abiabatic melting and recrystallization. The latter effect is the most important one in the case of tritium. Observing the fundamental law assumed (Equation (7)), it is clear that in this case the time constant τ is expected to be the determining parameter in describing the process.
(f) The importance of changing grain size in the snow column. Evidently the conditions for fractionation become unfavourable with increasing grain size. The mechanism of recrystallization must then become considerably slower. Our model could be improved to meet these conditions by simple amendments. We could assume a definite part of every solid-phase section not to participate in fractionation. This would not cause any difficulties in our equations nor the difference scheme.
Concluding remarks
Up to the present we have only applied our model to a very few cases. Considerably more information and experience is to be gathered. We can, however, already state that fractionation is occurring in melting snow columns. This is especially clear from comparison of measurements and computed results for laboratory experiments on deuterium concentration and for tritium concentrations on glaciers. The model should of course also apply to fractionation of 18O.
Acknowledgements
The author wishes to express indebtedness to Professor Th. Sigurgeirsson, Mr Bragi Árnason and Mr Páll Theodórsson for fruitful discussions and for allowing the use of data necessary for this work. To Dr Halldór Elíasson the author is grateful for encouragement and suggestions in dealing with the mathematical problem.














